上篇文章提到了数学中四个重要的常数, e(自然常数)、π(圆周率)、i(虚数单位)、1(自然数单位), 虽然我们发现它们很久了,但对它们性质的了解,目前还是知之甚少。直到18世纪,e和π这两个常数的无理性才被证明。而超越性的证明又要比无理性困难地多,又过了100年,也就是在 19世纪 人们更加了解超越数、超越函数之后,e和π的超越性才被证明。直到现在数学家只发现了屈指可数的超越数,虽然 超越数的数量要比代数数多的多 ,因为代数数是可数的,测度为0。这一篇先证明无理性。
记得我是在学微积分的时候开始考虑如何证明e是无理数的。我发现现在对数论感兴趣的中年人也很多,也许是在 年轻求学时播下了热爱数学的种子 ,却一直没有机会像数学家一样做数学。 纯粹数学的特点是它不依赖于任何外物 ,一支笔一张纸就可以徜徉数学王国了,类似高僧面壁打坐,进入心流状态,忘记时间,忘记烦恼。 虽然我们从小学一年级就开始学习数学,但老实说大多数人还没有入门,所以后期我也 打算写给中小学生的数学启蒙书,尽早地培养数学审美 ,即知道 什么是好数学什么是坏数学 ,数学是研究什么的?这样会避免走很多弯路。例如像背圆周率多少多少位、心算什么的其实与数学没多大关系。为了感谢读者支持,整理的 【华章数学译丛系列】 作为读者自学教材免费分享给读者,关注公众HAO:酷学在线课堂。或者向公众号发送消息「get」,就可以获得免费资料的链接。

先来证明e是无理数,它相对π来说容易一点。上一篇文章给出过指数函数的幂级数表示:

现在用反证法证明e是无理数。

取n>b,则有 0<M<1 ,则等式右边不是整数,等式不成立,矛盾!
从这个证明可看出,证明e是无理数,是用e的无穷级数形式来描述e,这样就可以在代数式中推出矛盾。e本来就是可用有理函数极限定义,它离有理数还不算远,而对于圆周率π来说,它的定义是圆的周长和直径的比,这是几何角度的定义。在分析学中可把它定义成满足sinx=0的最小正实数x,第一个将π表示成无穷级数的是莱布尼茨。
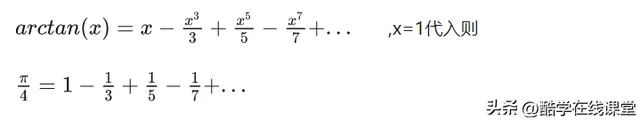
莱布尼茨让我们对π更加了解了。在1761年瑞士数学家兰伯特第一次证明e是无理数,这不是最简洁的证明,但我觉得很有趣,兰伯特用到了他那个时代流行但当代所废弃的数学工具: 连分式 ,我在前面的文章【为何作为无理数的黄金分割数可用循环的连分数表示?】介绍过连分式,现在几乎很难见到关于连分数的著作了,历来中学数学大纲都未将其包含进去。兰伯特从正切函数的连分式入手,首先他证明了一个命题: 非0有理数的正切值一定是一个无理数。
兰伯特把tan(x)写成无限连分数形式

假设x是非0有理数,不妨设 x=a/b ,要证明 tan(a/b) 是无理数。



证明了"非0有理数的正切值一定是一个无理数"之后,就可以用反证法证明最终的结论了,已知tan(π/4)=1,而1是有理数,所以π/4是无理数,推出π是无理数。
可以把连分式看作数列,例如计算tan(π/4),第一项为π/4,第二项为(π/4)/[1-(π/4)^2/3],当项数增大,这个数值越来越逼近tan(π/4)。感兴趣的读者可以思考其他证明e和π是无理数的方法。











