大家好,今天要講的內容是,誤差反向傳播演算法。
誤差反向傳播演算法,是神經網路中的學習難點。
而理解誤差反向傳播演算法,是理解神經網路模型訓練過程的關鍵一環。
希望這個篇文章,能幫助同學們,徹底弄懂誤差反向傳播演算法。
1.誤差反向傳播有什麽用
神經網路的訓練目標,是最小化網路的代價函式E。
為了找到使E取得最小值時的參數值,會使用梯度下降演算法。
而執行梯度下降演算法,就需要計算出E關於網路中各個參數w和b的偏導數:
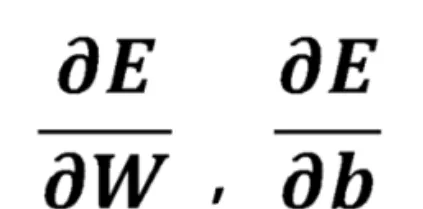
誤差反向傳播演算法,基於鏈式法則,將E關於參數的偏導數計算,分解為一系列簡單的步驟:

誤差反向傳播從輸出層開始,逐層的向前計算E關於各層之間參數的偏導數,最後到達輸入層。
由於這個過程是從後向前的,因此它被稱為「反向傳播演算法」。
誤差反向傳播演算法,有一個通用的公式:
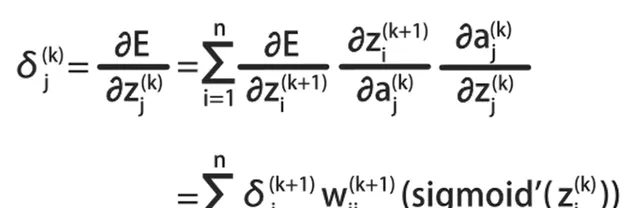
根據這個公式,可以計算E關於各層之間參數的偏導數:
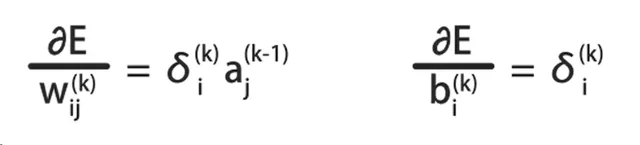
它是誤差反向傳播演算法的核心公式。
今天我們不討論這個公式的推導,而是使用一個具體的三層神經網路:

舉例說明誤差反向傳播的計算過程。
這裏會具體的計算出,E關於w1到w8,E關於b1到b4的偏導數:
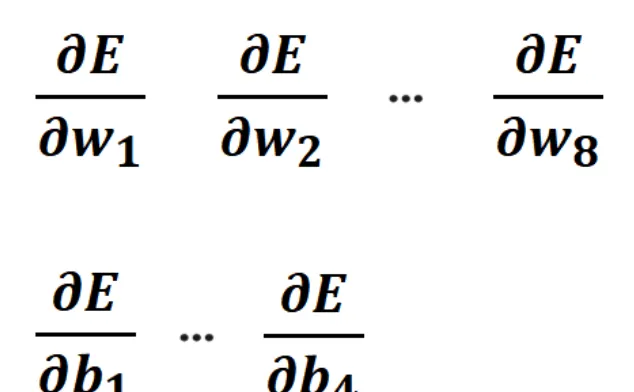
有了這些偏導數,就可以對這個神經網路,執行梯度下降演算法了。
2.神經網路的前向傳播
為了說明反向傳播演算法,需要先弄明白,神經網路前向傳播的計算過程。
在這個過程中,我們將使用計算圖來詳細說明這個神經網路。
在樣例神經網路中,使用sigmoid啟用函式和交叉熵誤差E:

其中x1和x2是輸入的特征值。
a1和a2是第2層神經元的輸出。
p1和p2是第三層的輸出。
另外,使用w1到w8表示8個w參數。
b1到b4表示4個偏置參數。
z1到z4表示4組線性累加和的結果。
3.畫出神經網路的計算圖
首先畫出輸入層到隱藏層的前向傳播計算圖:
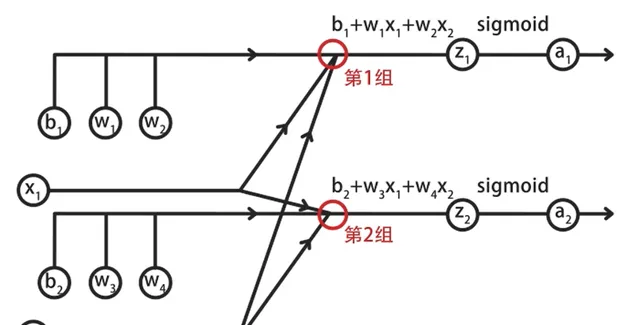
其中包括了兩組線性方程式求和,與sigmoid函式計算。
具體來說,在第一組計算中,輸入層的兩個特征x1和x2對應參數w1和w2。
將它們相乘後,再加上偏置b1等於z1,將z1代入到sigmoid中,得到a1。
按照同樣的方式,計算第2組的輸出。
其中,z2=x1*w3+x2*w4+b2,a2=sigmoid(z2)。
這樣就完成了輸入層到隱藏層的計算,結果是a1和a2。
然後畫出隱藏層到輸出層的前向傳播計算圖,其中同樣包括兩組計算:
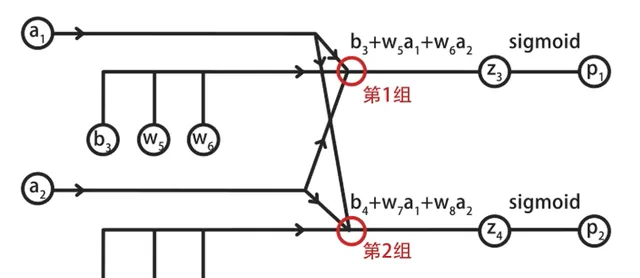
在第一組計算中,輸入的a1和a2與參數w5和w6相乘,再加上偏置b3,得到z3。
將z3代入到sigmoid,得到輸出層第1個神經元的輸出p1。
同理,可以計算出第2組的結果p2。
我們將這兩組計算圖合並,就得到了神經網路前向傳播的完整計算圖:
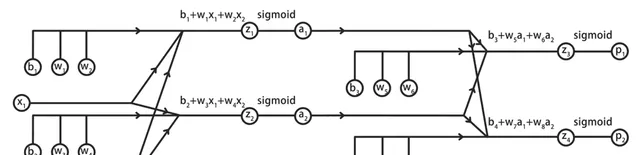
為了計算誤差E關於參數的偏導數,還需要將E加到計算圖中:
這裏我們只關註某一個樣本產生的誤差E,從而忽略掉西格瑪求和符號。
在輸出層中,包括兩個神經元,它們的人工標記結果是y1和y2,神經網路的輸出結果是p1和p2。
根據交叉熵誤差,分別計算兩個神經元的誤差,為E1和E2,總誤差E=E1+E2。
這樣,我們就得到了這個三層神經網路的完整計算圖:
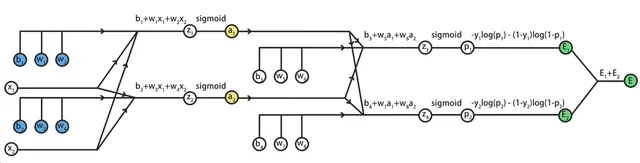
接下來,我們要根據這個計算圖,使用鏈式法則。
從後向前,推匯出代價函式E,關於參數w1到w8、b1到b4的偏導數。
這實際上,就是反向傳播演算法的手動計算過程。
4.誤差發現傳播演算法
先來研究神經網路的後半段,也就是w5、6、7、8對整體誤差E產生的影響。
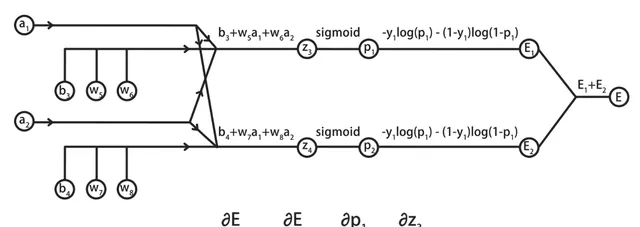
具體以w5為例,說明E關於w5的偏導數的計算過程。
在計算時,需要基於鏈式法則,將E關於w5的偏導數,拆解為E對p1、乘p1對z3、乘z3對w5的偏導數。
5.E關於w5偏導數的詳細計算過程
首先計算E對p1的偏導數:

在計算時,需要基於log函式的求導方法,計算結果為-y1/p1+(1-y1)/(1-p1),其中y1是常數。
然後計算p1對z3的偏導數:

在計算時,需要基於sigmoid函式的求導:

設g(z)為sigmoid函式,g(z)的導數為g(z)*(1-g(z))。
p1=sigmoid(z3),因此p1對z3的偏導數,就是p1*(1-p1)。
最後基於線性方程式,計算z3對w5的偏導數:
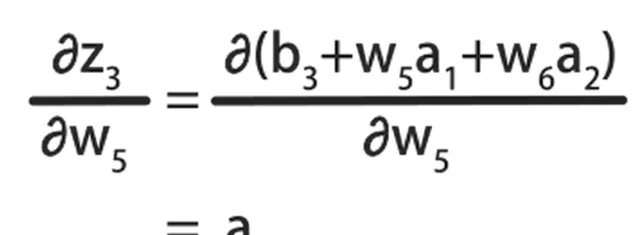
它等於w5的系數a1。
將三組計算結果相乘,消去重復的項,就得到了E對於w5的偏導數:
它等於神經元的輸出值p1減標記值y1乘對應的輸入特征a1。
仔細觀察可以發現,這個結果與邏輯回歸中的梯度計算結果是一樣的。
按照同樣的方式,可以計算出E對w6、w7、w8和b3、b4的偏導數:
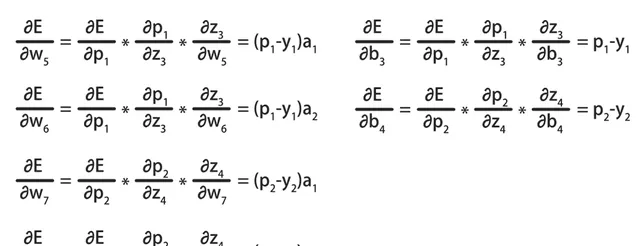
這種基於鏈式法則,從後向前計算偏導數的方式,就被稱為向後傳播演算法。
接下來,我們繼續推導E對於w1到w4,b1和b2的偏導數。
觀察計算圖的前半部份:
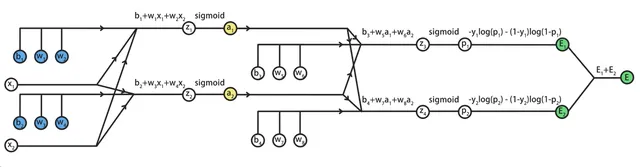
可以發現藍色標記的待求參數,會經過a1和a2,再傳導到E。
因此,如果可以先求出E對a1和a2的偏導數,再基於鏈式法則,就能推匯出E關於藍色參數的偏導數了。
6.E關於a1和a2的偏導數計算
在求E關於a1、a2的偏導數時,會發現z3、z4同時出現在a1、a2到E的路徑上:

這說明a1和a2與z3和z4都是有關系的。
因此我們需要先求出E對z3、z4的偏導數。
再求z3、z4對a1、a2的偏導數,最後合並到一起,得到結果。
我們將中間不相關的變量節點全部省略掉,得到了一個更簡單的計算圖:
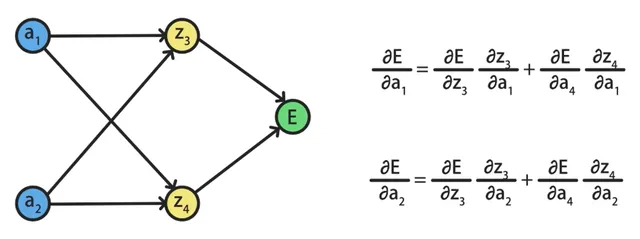
其中E對a1的偏導數,可以基於a1、z3、E和a1、z4、E兩條路徑計算。
而E對a2的偏導數,可以基於a2、z3、E和a2、z4、E兩條路徑計算。
我們已經推匯出E關於z3、z4的偏導數,它等於神經元的輸出值p減去該輸出對應的標記值y:

另外,z3和z4對於a1的偏導數,是a1的系數w5和w7。
z3和z4對於a2的偏導數,是a2的系數w6和w8。
求出鏈式法則需要的中間結果後,將它們代入到E關於a1和a2的偏導數公式中,就得到了最終的結果:
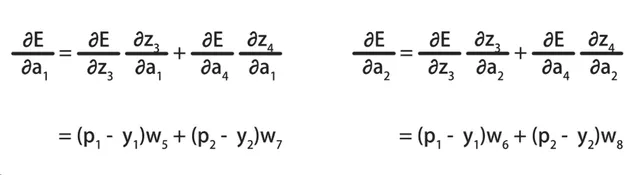
有了E關於a1和a2的偏導數後,就可以繼續透過鏈式法則,求出E關於參數w1到w4、b1和b2的偏導數了。
我們以E關於參數w1的偏導數,來說明計算過程:
根據鏈式法則,E對w1的偏導數,等於E對a1、a1對z1、z1對w1這三個偏導數結果的乘積。
其中E對a1的偏導數,已經求出,a1對z1是sigmoid函式求導。
而z1對w1求導,是w1對應的特征x1:
將這三個值相乘,就得到了E對w1偏導數的具體值了:
按照同樣的方法,可以繼續求出E對於w2、w3、w4和b1、b2的偏導數。
這樣我們就使用誤差反向傳播演算法,將E關於神經網路中所有參數的偏導數,都求出來了。
後面可以直接使用這些偏導數,進行梯度下降演算法的叠代。
那麽到這裏,誤差反向傳播演算法就講完了,感謝大家的觀看,我們下節課再會。











