編輯:Aeneas 好困
【新智元導讀】全新的勾股定理證明方法,竟然被兩個高中女生證明出來了?而且還一次給了五個方法!陶哲軒對這項工作稱贊不已:五個證明與已知證明沒有明顯相似。而故事的起因,竟是一道高中數學競賽題。內附兩人自述證明過程影片,亮點多多。
兩年前,兩位高中在讀的學生發現了全新的勾股定理證明方法。
遺憾的是,當時並沒有更具體的論文,以提供實質性細節。
就在最近,兩人的全新論文,在【美國數學月刊】上正式發表了!

論文地址:https://www.tandfonline.com/doi/full/10.1080/00029890.2024.2370240#abstract
在這篇論文中,兩位作者找到了至少五個證明,與任何標準的已知證明都沒有明顯的相似。
陶哲軒對這項工作稱贊不已。
他表示,怎樣精確定義兩個證明是否相同,是很微妙的。

以往的數學家證明勾股定理,用的多是代數或幾何的方法。
然而這兩個學生,卻采用了一種「三角學」的方法。(作為數學的一個分支,「三角學」主要研究的是三角形的變長和角度之間的關系,尤其是直角三角形。)
具體來說,她們采用了一種主要基於句法的方法:在她們看來,如果一個證明避免使用圓(或座標),但本質上使用角度,就可以被視為「三角學」證明。
就這樣,她們找到了至少5個不同的證明,比如其中一個證明就涉及幾何級數求和。

Ne’Kiya Jackson和Calcea Johnson
所以,是否存在「語意」方式,來區別這些證明呢?
陶哲軒表示,理論上這種方式應該是存在的,因為在某些歐幾裏得幾何的變種中,或許本文中的證明有的有效,有的無效,反之亦然。
但即使有沒有這種語意方式做區分,兩位學生的研究仍然非常引人入勝。
因為——即使是數學中最古老、最基礎的結果,有時也可以找到全新的證明角度!
仔細看這個影片,你會註意到真正懂數學的高中生講起數學題來,是怎樣的語氣和神情。
古老的勾股定理
勾股定理(亦稱畢達哥拉斯定理)是平面幾何中一個基本而重要的定理,也是人類早期發現並證明的重要數學定理之一:
平面上的直角三角形的兩條直角邊的長度(較短直角邊為勾長、較長直角邊為股長)的平方和等於斜邊長(弦長)的平方。反之,若平面上三角形中兩邊長的平方和等於第三邊邊長的平方,則它是直角三角形(直角所對的邊是第三邊)。
勾股定理可考的嚴謹數學證明,起源於歐幾裏得【幾何原本】中卷一的命題47。
如今,已經有了四百多個證明,諸如微分證明、面積證明等。

一道高中競賽題,500美元獎金
有趣的是,這項震驚數學圈的證明,催化劑竟是一道高中數學競賽的附加題。

這道題要求找出一種全新的勾股定理證明方法(真是一個敢想,一個敢做)
因為有500美元獎金,兩位學生決定嘗試一把。
結果兩人發現,這比想象的要困難得多……
她們度過了很多個不眠之夜,嘗試找到一個證明,卻屢屢失敗。
好在經過一個月的腦力大爆炸後,兩人都找出了新的解法。

她們高中的數學誌願者Rich認為,她們的證明足夠新穎,足以在數學會議上展示,因為通常只有專業數學家和大學生才會受邀。
她們開始並沒有信心,但還是決定參與。就是這時兩人開始展開合作。
接下來的兩三個月,兩人把課後、周末、假期的所有時間都用來打造這篇論文。
令人驚訝的是,兩位高中生的作品得到了認真對待,並被批準在2023年3月的美國數學學會東南分會會議上展示——於是兩人成為房間裏最年輕的演講者。
隨後,AMS鼓勵兩人把研究成果送出到學術期刊。
兩人從沒有為學術期刊寫論文的經驗,同時還在適應大學環境,需要應付小組論文、實驗室數據分析、學習用LaTeX寫程式碼等等任務。
兩人表示,在家人和社區的支持下,我們堅持了下來,這段路途絕對不是簡單的。
沒有現成的路線圖,沒人保證論文一定能發表。
有很多次,她們都想放棄這件事,好在最終,兩人堅持了下來。
令人困惑的三角學
而在這次發表的研究中,兩位學生介紹道:在數學中,或許沒有哪個學高比三角學更讓高中生感到困惑了。
三角學為什麽如此令人困惑?或許一個原因是,存在兩種不同的方法來定義相同的三角學術語。
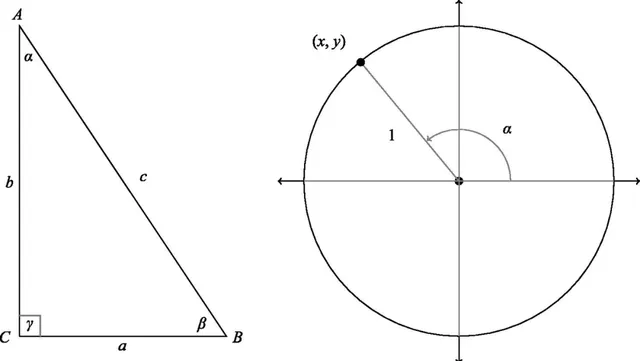
圖1倒是展示了這些方法是如何被協調的,但結果卻適得其反——
學生們或許不會意識到,這兩個互不相同的三角學體系,已經被套在了相同的術語上,所以理解起來極其困難。
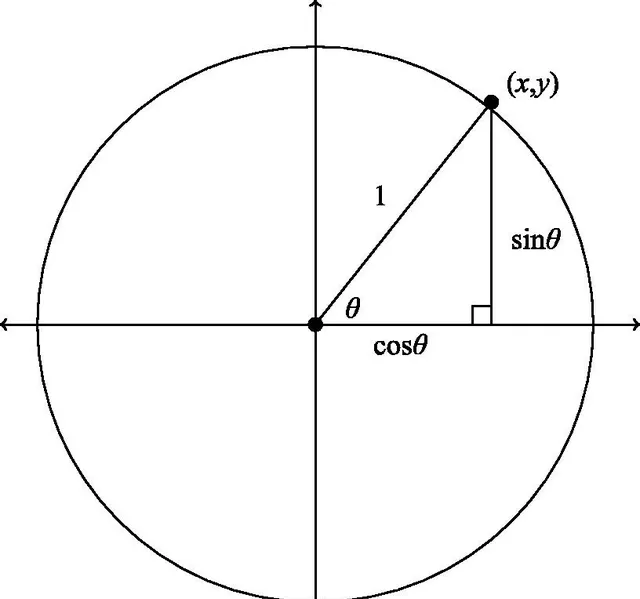
圖1:被作者稱為「數學中危害最大的圖」
兩位作者表示,避免混淆最合理的方法,就是給它們不同的名稱,來反映背後不同的理念。
實際上,這些方法中只有一種是三角學的,專註於這個真正的版本,就可以發現大量全新的勾股定理證明!
何為三角函數證明
「trigonometry」這個詞來源於希臘詞「trigonon」(三角形)和「metron」(測量),因此三角函數是透過測量三角形而得到的。
實際上,三角比中的正弦(sine)和余弦(cosine)定義為銳角的函數,其方法是建立一個直角三角形ABC,使得為其中一個銳角(如圖2左側所示),然後比較三邊中兩條邊的長度關系。
sin被定義為對邊BC與斜邊AB的比值,cos則是鄰邊AC與斜邊AB的比值。
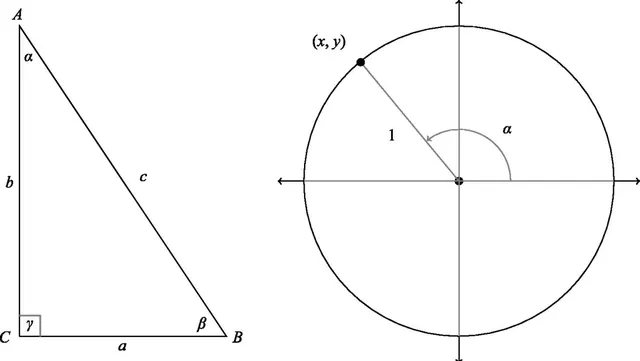
圖2:正弦和余弦的三角函數和圓周定義
然而,這種正弦和余弦的定義法僅適用於銳角,其他角度則需要完全不同的方法。
對於這些角度,就要使用單位圓,從點(1,0)開始,逆時針方向(對於負角則順時針)沿圓周移動,直到達到所需的中心角,最終到達點(,),然後定義cos=和sin=。
對於銳角來說,這來年各種方法得出的值是相同的,如圖1所示。
然而,只有第一種方法可以被合理地稱作「三角學」,第二種方法更適宜被叫做「圓周法」,源自希臘詞「circle」和「location」。(圖2)
它們的區別,意味著透過余弦定律證明畢達哥拉斯定理(我們從²=²+²−2 cos 開始,並令為直角)是圓周證明而不是三角證明:因為三角學無法計算直角的余弦,而圓周測量告訴我們cos(90°)=0。
同樣地,使用cos(−)公式證明畢達哥拉斯定理(在恒等式cos(−)= cos cos + sin sin 中,令=)也是圓周法而非三角學,使用sin(+)公式的證明亦然,其中和為互余角。
另外,某個證明是否屬於三角學,也可以因其他原因被否認。
例如,如圖3所示,畢達哥拉斯定理的最著名的證明之一,就使用了相似三角形△∼△∼△:由於/=/和/=/,所以=+=²/+²/,因此²+²=²。
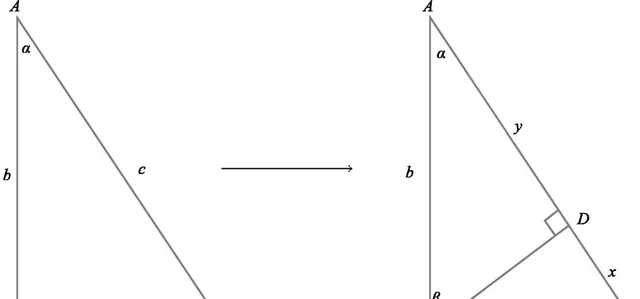
圖3:透過相似三角形的證明
但這個證明很容易被覆寫為三角學。
由於/=/= sin ,因此有= sin =( sin ) sin = sin² ,同樣地,= cos² 。
然後=+= (sin² + cos² ),由此得1= sin² + cos² =(/)²+(/)²,因此²+²=²。
但是,在這裏使用三角術語並沒有增加任何實質內容——實際上只是復混成了對同一方法的簡單視角,因此可以說,這個證明使用了相似三角形而不是三角學。
更一般地,任何證明²+²=²的方法,都可以透過 sin 為a和 cos 為b(或透過將邊長a, b和c重新縮放為 sin , cos 和1)來重新表述為「三角」證明:首先證明 sin² + cos² =1,然後透過反向替換 sin =/和 cos =/來證明²+²=²。
這種現象表明,這種迂回的畢達哥拉斯定理的「三角」證明值得被懷疑(即首先證明恒等式 sin² + cos² =1),不然,「三角學」就僅僅是用正弦和余弦對邊長的重復敘述罷了。
兩位作者表示,事實上,她們也不知道如何在畢達哥拉斯定理的「三角」證明和非三角證明之間劃清界限。
但根據設定的標準,就可以有一個起點,按照這個標準,兩個畢達哥拉斯定理的證明可以算作三角函數的證明。
第一個證明來自J. Zimba,使用了復角公式的代數性質,證明了對任意銳角,都有 sin ² + cos² = 1。
另一個證明來自N. Luzia,他使用了復角公式和半形公式,證明了對於任意銳角,都有 sin²(/2) + cos²(/2) = 1。
註意,當角度/2為45°時,Luzia的方法在等腰直角三角形上不成立,但在45°</2<90°時有效,因為此時sin²(/2) + cos²(/2) = cos²(90°−/2) + sin²(90°−/2) = 1。
勾股定理的五個新證明
至此,兩位學生就證明了對於等腰直角三角形的勾股定理,由此開始了勾股定理的五個新證明。
在以下五個證明中的前四個中,她們假設ABC是一個非等腰直角三角形,其中<,或者<45°<。
每個證明都從一個直角三角形的圖形開始。
證明1


證明2
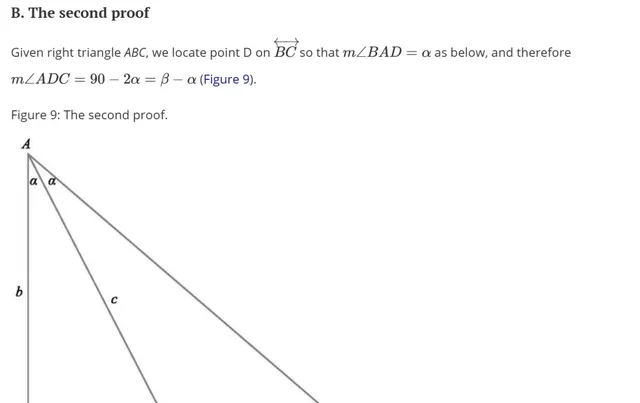

證明3
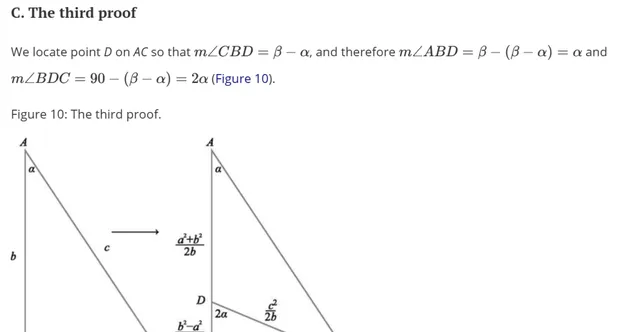

證明4
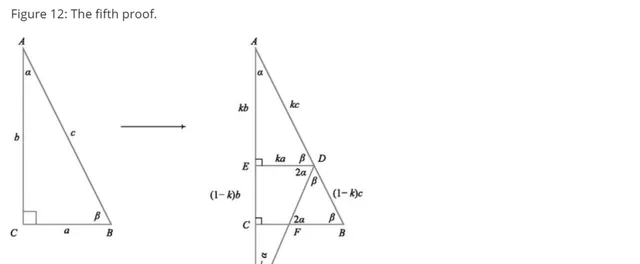

證明5

方法
在任何創造性活動中,一個基本問題是:「我能用現有的東西創造出什麽?」
在勾股定理中,這個問題就變成了:「我能用給定的直角三角形ABC,創造出什麽樣的直角三角形?」
為此,作者將新三角形的建立限制在一個條件下:其角度是△的三個角、和90°(=+)的整數和/或差。
這樣一來,問題的答案就簡單了。
引理1:
如果ABC是一個等腰直角三角形(==45),那麽唯一的角度為和的整數線性組合的三角形是等腰直角三角形。
在直角三角形ABC中,如果 < ,則存在一個直角三角形,其銳角為2和−。此外,2和−是和的唯一整數線性組合,它們將形成每對{,}的直角三角形的銳角。
證明:
a. 由於等腰直角三角形ABC的所有角度都是45的倍數,因此任何新三角形(其角度限制為△的角度的和/或差)的所有角度仍然是45的倍數,因此這個三角形必須是等腰直角三角形。
換句話說,如果我們從一個等腰直角三角形開始,不可能創造出一個新三角形。
b. 現在假設 < 。
如果新構建的直角三角形的一個銳角為 + (,∈ℤ),那麽它的補角為90 – ( + ) =(+)–( + ) = (1−) + (1−)。
如果整數n和1−都不為零,且其中一個(比如n)是負的,那麽用⏧⏧替換n,我們看到其中一個角度為 – ,其中m>n>0。
但是當為90/(+)度時,它的補角為90/(+),這種構造給我們一個角度為 – = 90/(+) – 90/(+)=0的三角形。
這種不可能性表明必須有=0,因此其中一個銳角測量為,對於某個∈ℕ。
如果=1,那麽我們簡單地恢復了原來的三角形ABC。
如果=2,那麽我們得到一個新的直角三角形,其銳角測量為2和 – 。(註意2<90,因為<45。)
最後,我們看到≥3是不可能的,因為如果30≤<45,則不存在這樣的三角形。
這項引理準確地指引我們尋找勾股定理的證明(對於非等腰直角三角形):從原來的三角形ABC開始,我們嘗試以盡可能多的方式創造一個新的直角三角形,其角度為2, – 和90度。
例如,創造一個2角的顯而易見的方法是將兩個△結合在一起,如圖13所示。

圖13:創造一個2角
這樣就建立了一個等腰三角形′,其角度分別為2、和,因此下一步是將其中一個角轉化為 – 或90度(圖13)。
為了在頂點′形成一個90度的角,我們構造了一條與′成角的射線。延長邊AB至與射線在點D相交,就得到了第一個證明的圖形(圖14)。
圖14:建立第一個證明
或者,如果我們在斜邊AB的另一側構造一個2角,並延長BC至與新射線在點D相交,如下所示,就得到了直接指向第二個證明的圖形(圖15)。
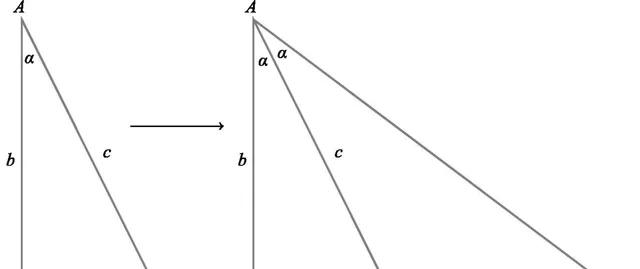
圖15:建立第二個證明
這種簡單的方法產生了多個新的證明,其中五個如上圖所示,而另外五個或者更多證明方法,可以留待讀者去發現。
參考資料:
https://www.tandfonline.com/doi/full/10.1080/00029890.2024.2370240#d1e4959











