上篇文章提到了數學中四個重要的常數, e(自然常數)、π(圓周率)、i(虛數單位)、1(自然數單位), 雖然我們發現它們很久了,但對它們性質的了解,目前還是知之甚少。直到18世紀,e和π這兩個常數的無理性才被證明。而超越性的證明又要比無理性困難地多,又過了100年,也就是在 19世紀 人們更加了解超越數、超越函數之後,e和π的超越性才被證明。直到現在數學家只發現了屈指可數的超越數,雖然 超越數的數量要比代數數多的多 ,因為代數數是可數的,測度為0。這一篇先證明無理性。
記得我是在學微積分的時候開始考慮如何證明e是無理數的。我發現現在對數論感興趣的中年人也很多,也許是在 年輕求學時播下了熱愛數學的種子 ,卻一直沒有機會像數學家一樣做數學。 純粹數學的特點是它不依賴於任何外物 ,一支筆一張紙就可以徜徉數學王國了,類似高僧面壁打坐,進入心流狀態,忘記時間,忘記煩惱。 雖然我們從小學一年級就開始學習數學,但老實說大多數人還沒有入門,所以後期我也 打算寫給中小學生的數學啟蒙書,盡早地培養數學審美 ,即知道 什麽是好數學什麽是壞數學 ,數學是研究什麽的?這樣會避免走很多彎路。例如像背圓周率多少多少位、心算什麽的其實與數學沒多大關系。為了感謝讀者支持,整理的 【華章數學譯叢系列】 作為讀者自學教材免費分享給讀者,關註公眾HAO:酷學線上課堂。或者向公眾號發送訊息「get」,就可以獲得免費資料的連結。

先來證明e是無理數,它相對π來說容易一點。上一篇文章給出過指數函數的冪級數表示:

現在用反證法證明e是無理數。

取n>b,則有 0<M<1 ,則等式右邊不是整數,等式不成立,矛盾!
從這個證明可看出,證明e是無理數,是用e的無窮級數形式來描述e,這樣就可以在代數式中推出矛盾。e本來就是可用有理函數極限定義,它離有理數還不算遠,而對於圓周率π來說,它的定義是圓的周長和直徑的比,這是幾何角度的定義。在分析學中可把它定義成滿足sinx=0的最小正實數x,第一個將π表示成無窮級數的是萊布尼茨。
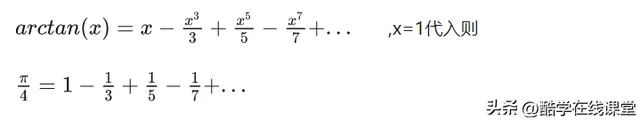
萊布尼茨讓我們對π更加了解了。在1761年瑞士數學家蘭伯特第一次證明e是無理數,這不是最簡潔的證明,但我覺得很有趣,蘭伯特用到了他那個時代流行但當代所廢棄的數學工具: 連分式 ,我在前面的文章【為何作為無理數的黃金分割數可用迴圈的連分數表示?】介紹過連分式,現在幾乎很難見到關於連分數的著作了,歷來中學數學大綱都未將其包含進去。蘭伯特從正切函數的連分式入手,首先他證明了一個命題: 非0有理數的正切值一定是一個無理數。
蘭伯特把tan(x)寫成無限連分數形式

假設x是非0有理數,不妨設 x=a/b ,要證明 tan(a/b) 是無理數。



證明了"非0有理數的正切值一定是一個無理數"之後,就可以用反證法證明最終的結論了,已知tan(π/4)=1,而1是有理數,所以π/4是無理數,推出π是無理數。
可以把連分式看作數列,例如計算tan(π/4),第一項為π/4,第二項為(π/4)/[1-(π/4)^2/3],當項數增大,這個數值越來越逼近tan(π/4)。感興趣的讀者可以思考其他證明e和π是無理數的方法。











