關於歐拉公式,我寫了很多文章,但這是一個百談不厭的話題,因為它確實太美麗,太吸引人了。一個只有四個字元的等式,包含的資訊量是驚人的,並且意義也非常深刻。這篇文章,我們將一起看看歐拉公式是如何擴充套件e的定義的。
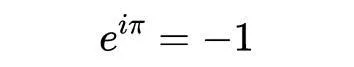
很多人第一次看到這個公式都會感到震驚。為什麽這個等式可以成立?這幾乎就是復數的定義,我們可以這樣寫:

它擴充套件了e的定義,使之對復數有意義 ,同時對實數仍然有意義。首先,讓我們先理解方程式的右邊,它與初級幾何學有很好的聯系。
復數的視覺化
我們可以把復數看作二維平面上的一個點,用半徑和角度來描述,或者用x座標和y座標來定義。Y軸對應的是 "虛軸",X軸對應的是 "實數軸"。所以點(2,3)對應於2+3i,其中i是-1的平方根。
兩個復數相加對應的只是將它們的實部和虛部相加。例如,(2+3i)+(1+5i)=(3+8i)。
復數的乘法可以用一種有趣的方式來形象化: 它對應於旋轉和半徑的變化 。在這裏,-1的平方根是完全有意義的,因為我們已經擴充套件了乘法的定義。點 i 的角是90度,長度是1。所以,當點z乘以 i 時,相當於將點z旋轉90度,並將長度擴大1倍。當然,半徑乘以1還是不變的。如果用2i乘以z,它就會旋轉90度,向外拉伸2倍。
現在,我們做一件有趣的事情,把定義在實數上的e的規則也用在復數上,看看會發生什麽!讓我們把兩個數碼相乘。然而,我們做的事情有點奇怪。我們把復數寫成下面的形式:
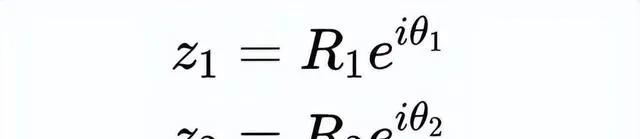
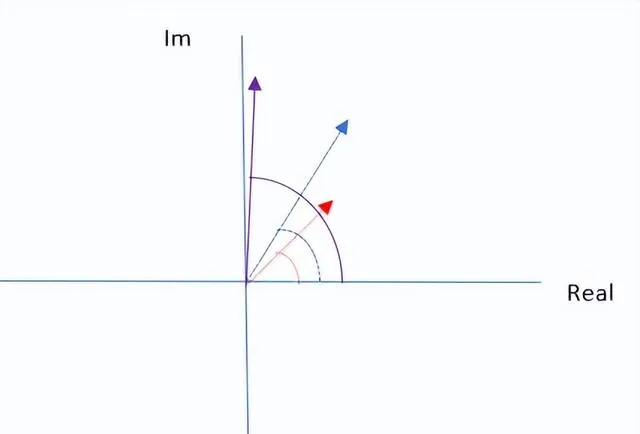
z_1是藍色的線,角度和半徑較大,z_2是紅色的線,角度和半徑較小。

現在我們將它們相乘,同時顯示出視覺上和代數上的情況。
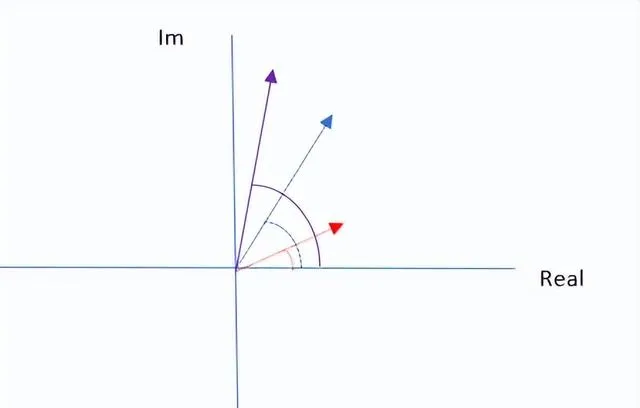
從視覺上看,當我們把紅線和藍線(或 "向量")"相乘 "時,會得到紫色的線。
在復數乘法中,我們將角度相加,並將半徑相乘。紫線的角度是紅線的角度和藍線的角度之和。紫色線的長度是紅色線的長度與藍色線的長度的乘積。
現在讓我們直觀地看看,當旋轉紅線時,紫線會發生什麽變化。下圖顯示,它的長度保持不變,但紫線的旋轉量與紅線的旋轉量相同。
現在,讓我們用一些代數來正式說明這一點:
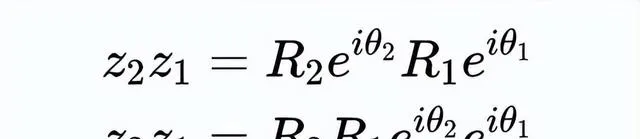
我們看到有兩個e乘在一起,對於實數:
所以我們試試用同樣的規則來處理復數(還沒有正式證明)。對復數使用同樣的規則:
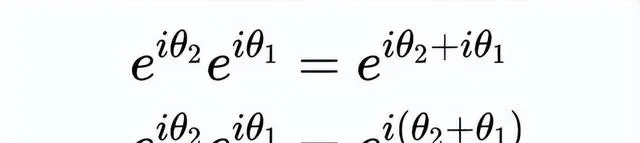
所以總的來說,我們得到了這個結果:
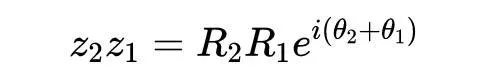
因此,在代數上我們得到了我們所看到的視覺效果! 為了算出兩個復數的乘積,我們把它們的角度相加,再乘以它們的半徑。
e,sin,cos
現在我們來看看我們是如何寫復數的。我們可以用實部和復部來表達,也可以用半徑和角度來表達。我們如何將這兩者聯系起來呢?
我們先寫z = x + iy
現在,看看這兩種表示方法。

左邊的圖片是把復數寫成實部和虛部之和。右邊的圖片,用三角函數的定義將其轉換為用cos和sin來寫這兩個部份。
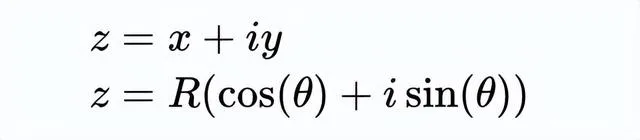
這看起來很簡單。 現在,神奇的一幕出現了。
這就是歐拉的天才之處 。 他擴充套件了e的定義,使之與定義在復數上的運算自然地配合。 (如果你學習了關於冪級數的課程,就會更加明白他的想法有多麽不可思議)。
數學中最著名的一行
現在,我們來看一下數學中最著名的一行文字(符號):

讓我們用我們的新工具來解讀它:
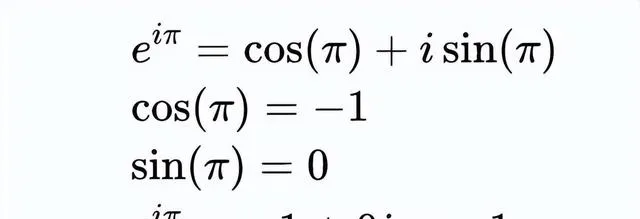
這個公式突出了歐拉在e和復數之間的聯系之美,但實際上,一旦我們理解了定義和符號,就不會覺得那麽復雜了。 我們所做的只是將一個數碼從半徑和角度的表示轉換為實部+虛部的表示。
故事並沒有到此結束。 這個公式暗示了復數世界將是多麽的神奇 。然而,直到19世紀,數學家(特別是柯西和黎曼)才揭開了復數中微積分的秘密。
冪級數,以及擴充套件 "e "的定義
冪級數提供了一個很好的方法來擴充套件e、sin和cos的定義,從它們作為實數到實數的函數的定義,擴充套件到它們在複數平面上的定義。
這表明歐拉的定義確實與實數的定義完美地結合在一起。
e^x、sin(x)和cos(x)都可以被定義為一個冪級數。
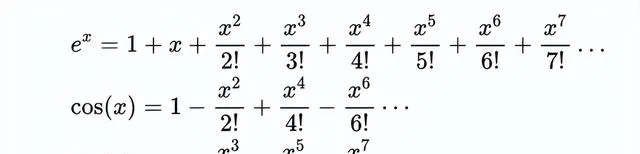
這意味著,對於每一個點x,這些函數的值都可以透過上面的無限級數來估算。
現在,回想一下,i^2=-1,是我們研究復數的開端。那麽我們為什麽不試試下面的方法呢?
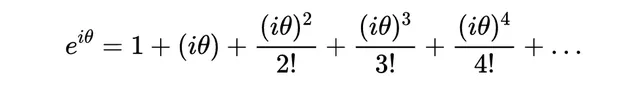
我們需要簡化i的所有冪:

這個規律會重復出現。例如:
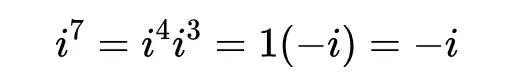
所以我們要進行化簡:

現在我們把實部和虛部份開:
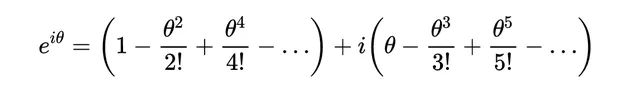
記得sin和cos的冪級數定義嗎?如果我再寫幾個術語,你就會想起我在本節開始時寫的冪級數。

我再給你最後一次機會來發現它:
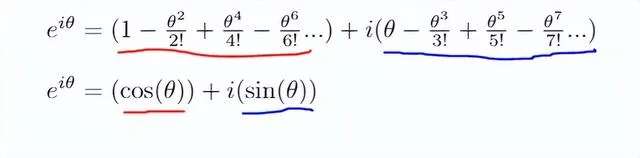
太神奇了!!
事實證明,有了我們對 i 的定義,有了我們對cos、sin和e的冪級數定義,這個公式就非常合理了。復數乘法的幾何定義不僅看起來很酷,而且驚人地將e的值與cos和sin聯系起來。
最後
誰能想到呢! 希臘人創造的描述圓上座標的函數(cos和sin)與e有神秘的聯系,一旦我們把數碼擴充套件到包括負1的平方根,它就會向自身微分。
這是個奇妙的世界。











