量子漲落的現實早在1947年就得到了證明

如果你花足夠的時間聽理論物理學家的話，就會開始聽起來像是他們居住著兩個獨立的世界。

1. 真實的、實驗和觀察的世界，充滿了數量和內容，我們可以透過足夠的設定進行高精度測量。

2. 它背後的理論世界，充滿了深奧的計算工具，這些工具可以模擬現實，但只能用數學術語來描述它，而不是純粹的物理術語。

最明顯的例子之一是虛擬粒子的概念。從理論上講，既有存在於我們的實驗中並且可以測量的真實粒子，也有存在於所有空間中的虛擬粒子，包括空白空間（沒有物質）和被占用的（包含物質的）空間。虛擬粒子不會出現在我們的探測器中，不會與真實粒子碰撞，也無法直接看到。作為理論家，我們經常告誡不要過於認真地對待虛擬粒子的類比，指出它們只是一種有效的計算工具，而且在我們的生活現實中，沒有實際的粒子「對」突然出現。

然而，虛擬粒子確實以重要的、可測量的方式影響著現實世界，事實上，它們的效應早在1947年就被發現，當時理論家甚至還沒有意識到它們的必要性。這是一個非凡的故事，講述了我們如何證明量子漲落必須是真實的，並且對我們測量的世界產生真正的影響，甚至在我們理解它們背後的理論之前。

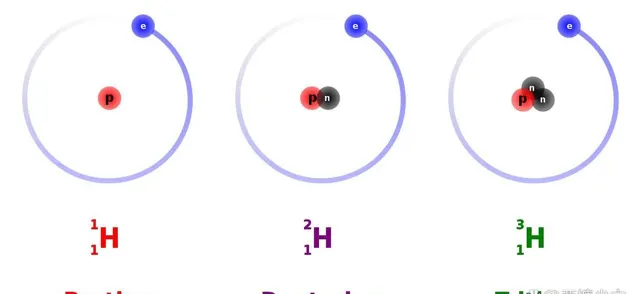
想象一下最簡單的原子：氫原子。在許多方面，這是量子理論的「試驗場」，因為它是宇宙中最簡單的系統之一，由一個帶正電的質子和一個與之結合的電子組成。是的，質子很復雜，因為它本身是由誇克和膠子結合在一起的，但出於原子物理學的目的，它通常可以被視為具有一些量子特性的點粒子：

當電子與質子結合時，它會形成一個中性氫原子，整個系統的靜止質素比自由質子和自由電子的總和略小。如果你把一個中性氫原子放在天平的一側，把一個自由電子和自由質子放在另一個尺寸上，你會發現中性原子輕了大約2.4×10 -35 kg：一個微不足道的數額，但仍然是一個非常重要的數目。

這種微小的質素差異來自這樣一個事實，即當質子和電子結合在一起時，它們會釋放出能量。發射的能量以一個或多個光子的形式出現，因為只有有限數量的明確能階是允許的：氫原子的能譜。當最初激發的電子透過各種能階向下級聯時，最終過渡到（最終）允許的最低能態（稱為基態），光子被釋放出來，該光子的能量、頻率和波長由電子在躍遷前後占據的不同能階決定。

如果你要捕捉從自由質子和自由電子向下過渡到基態氫原子過程中發射的所有光子，你會發現總是釋放出完全相同的總能量：13.6電子伏特，或者說可以將一個電子的電勢提高13.6伏特的能量。這種能量差正是自由電子和質子與束縛基態氫原子之間的質素等價差，你可以從愛因斯坦最著名的方程式中計算出來： E = mc² 。

根據支配宇宙的量子規則，原子中的束縛電子與自由電子有很大不同。

事實上，我們之所以稱它為「量子物理學」，正是源於這種現象：束縛粒子可以占據的能階是量子化的，並且只能以遵守束縛態規定的數學規則的特定量出現。

然而，處於基態的電子——記住，最低能量狀態——不會在特定時間出現在特定位置，就像圍繞恒星執行的行星那樣。相反，計算電子的概率分布更有意義：在任何特定時刻在特定位置找到電子的機率，在空間和時間上平均。請記住，量子物理學本質上與經典物理學不同：你無法準確測量粒子的位置和運動方式，而只能知道這兩種內容的組合，以達到某種特定的、有限的精度。更精確地測量一個本質上會導致對另一個的了解不那麽精確。

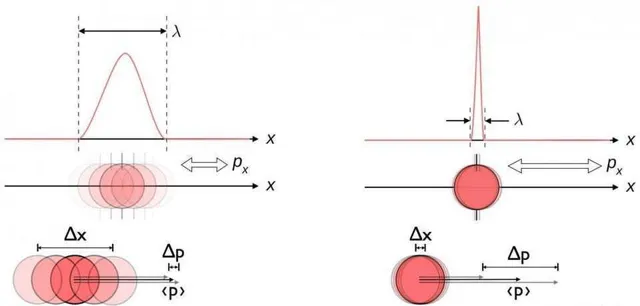
因此，我們最好不要把電子看作是一個粒子，當它處於氫原子中時，而應該是一個「概率雲」或其他一些類似的模糊視覺化。對於最低能量狀態，電子的概率雲看起來像一個球體：你最有可能在離質子中間距離的地方找到它，但你有可能在很遠的地方甚至在中心找到它：在質子本身內。然而，在你進行關鍵測量之前，更準確地用概率來描述電子的特性：占據一組具有特定概率振幅的值，而不是在任何時刻都有特定的位置和動量。

換句話說，決定其能量的不是電子在任何時刻的位置;相反，它是電子所占據的能階，它決定了每次進行測量時你最有可能和最不可能找到那個電子的相對概率。

但是，您可能找到電子與質子之間的平均距離與原子內電子的能階之間存在關系。這是尼爾斯·玻爾（Niels Bohr）的重大發現：電子占據離散的能階，在他的簡化模型中，這些能階對應於與原子核的特定距離的倍數。

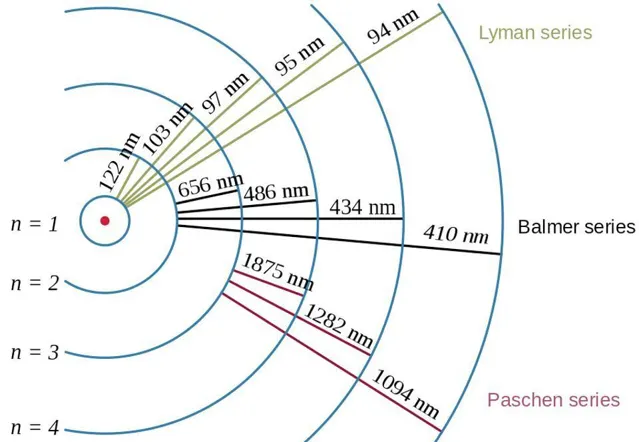
玻爾模型對於確定電子可以占據的氫原子的各個層次之間的躍遷能量非常有效。如果你有一個處於第一激發態的電子，它可以向下躍遷到基態，在這個過程中發射出一個光子。基態只有一個電子可以占據的可能軌域：1S 軌域，它是球形對稱的。該軌域最多可以容納兩個電子：一個自旋為 +1/2，另一個自旋為 -1/2，與質子的自旋對齊或反對齊。在氫原子的基態（第一能階）狀態下，電子沒有其他可能性。

但是當你跳到第一個激發態時，現在電子可以占據多個軌域，這對應於我們大多數人在元素周期表上熟悉的排列。

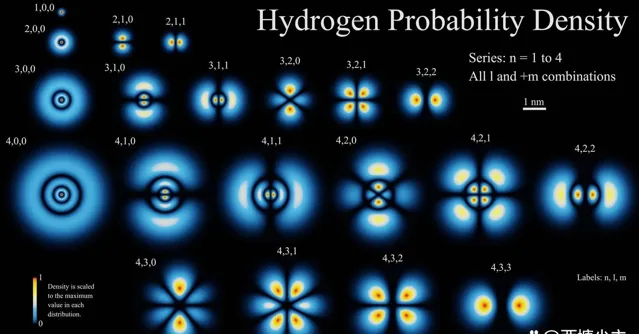
這些能階在玻爾1913年的模型之前就已經知道了，可以追溯到巴爾默1885年對光譜線的研究。到1928年，狄拉克提出了第一個包括電子和光子在內的量子力學相對論理論，表明——至少在理論上——如果它們之間的自旋或軌域角動量不同，那麽應該對這些能階進行校正：例如，在各種3D和3P軌域之間透過實驗確定的校正。（您可以在上圖中直觀地看到這一點，因為 3,1,0 和 3,1,1 對應於 3P 軌域，而 3,2,0、3,2,1 和 3,2,2 對應於 3D 軌域。

然而，在玻爾和狄拉克的理論中，2S 軌域和 2P 軌域中的電子應該具有相同的能量。是嗎？幾十年來我們一直不知道，因為直到1947年威利斯·蘭姆（Willis Lamb）和羅拔·雷瑟福德（Robert Retherford）進行了一個非常聰明的實驗，我們才對此進行了測量。

他們所做的是在基態（1S）中制備一束氫原子，然後用電子撞擊該束，使一些原子達到2S狀態。在正常情況下，這些 2S 電子需要很長時間（幾百毫秒）才能過渡回 1S 狀態，因為你必須發射兩個光子（而不僅僅是一個）來防止你的電子經歷被禁止的自旋躍遷。或者，您可以將這些激發的原子與一塊鎢箔碰撞，這會導致具有 2S 電子的原子去激發，從而發出可檢測的輻射。

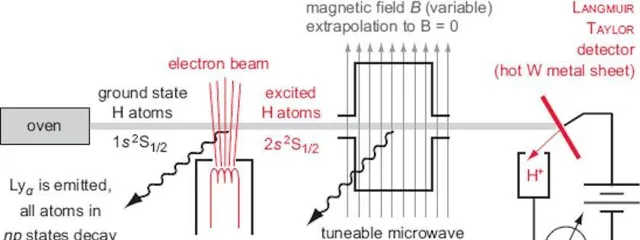
另一方面，處於 2P 狀態的電子應該躍遷得更快：在大約 ~1 納秒內，因為它們只需要發射一個光子進行量子躍遷，並且沒有量子規則禁止發射一個這樣的光子。蘭姆和雷瑟福德使用的聰明技巧是添加一個可以調諧的諧振器，用電磁輻射轟擊現在激發的電子。當電磁頻率剛好達到1 GHz以上時，一些被激發的氫原子立即開始發射光子（在納秒內），去激發回到1S狀態。

在正確的頻率下，可探測到的輻射立即下降是一個巨大的驚喜，提供了強有力的證據，證明這些原子已被激發到2P狀態，而不是2S狀態。

想想這意味著什麽：如果沒有這種額外的輻射，被激發的電子只會進入2S狀態，永遠不會進入2P狀態。只有加入載能輻射，才能將電子從2S態誘導到2P態。這意味著額外的輻射必須被電子吸收，並且額外的能量吸收將它們從 2S 狀態「提升」到 2P 狀態。

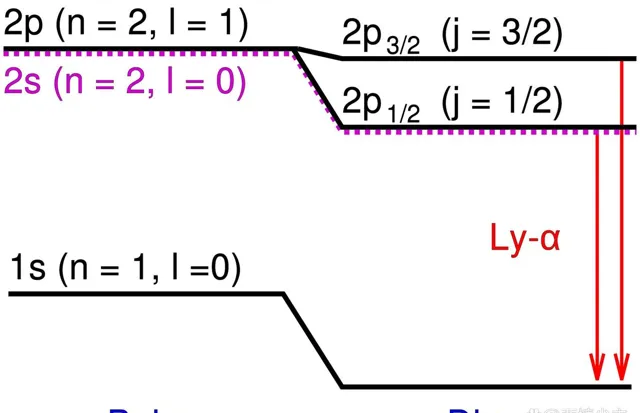
如果你還沒有意識到的話，其含義是驚人的。盡管我們理解了玻爾、狄拉克和量子理論的預言，但 2P 態的能量與 2S 態的能量不同。2P狀態的能量略高——今天被稱為 蘭姆位移 ——這是蘭姆和雷瑟福德的工作清楚地證明的實驗事實。目前尚不清楚為什麽會這樣。

一些人認為它可能是由核相互作用引起的;事實證明這是錯誤的。其他人則認為真空可能會變得兩極分化，但這也是錯誤的。

相反，正如 漢斯·貝特（Hans Bethe ）在那年晚些時候首次展示的那樣，這是因為原子的所有能階都是 透過電子與他所謂的「輻射場」的相互作用而改變 的，這只能在量子場論中正確解釋，例如量子電動力學。由此產生的理論發展帶來了現代量子場論，以及與虛擬粒子的相互作用——量化「輻射場」效應的現代方法——提供了蘭姆在1947年測量的確切效應，包括正確的符號和大小。

量子場本身存在著固有的非零能量：包括來自電動力學的輻射場、來自強核力的色動力學場以及來自弱核力的弱場。在我們的計算中，它們表現為出現在費曼圖中的虛擬粒子。它們不容忽視，它們的影響在被預測之前就已經被首次測量了：1947年，透過蘭姆班。

Lamb-Retherford實驗的結果足以證明量子漲落的真實效應的存在。我們可以這樣概念化它：原子本身始終存在，它施加電磁力，即庫侖力，它控制靜電吸重力。電磁場中的量子漲落導致其位置的電子漲落，這導致平均庫侖力與沒有這些量子漲落時的平均庫侖力略有不同。由於 2S 和 2P 軌域的幾何形狀略有不同，這些量子漲落——表現為來自原子中帶電粒子的虛擬光子——對軌域的影響不同，導致了今天已知的 蘭姆位移 物理現象。

可以肯定的是，束縛電子的位移和自由電子的位移之間肯定存在差異，但即使是自由電子也註定要與量子真空相互作用。無論你走到哪裏，你都無法逃脫宇宙的量子本質。今天，氫原子是量子物理學規則最嚴格的試驗場之一，它為我們提供了精細結構常數的測量值—— α ——優於1,000,000分之一。宇宙的量子性質不僅延伸到粒子，也延伸到場。這不僅僅是理論;我們的實驗已經證明了這一不可避免的現實超過四分之三個世紀。