考拉茲猜想(又稱為奇偶歸一猜想、3n+1猜想)是一個深刻的數學未解難題,以其簡單直觀的定義和證明上的巨大挑戰吸引了無數數學愛好者和專業數學家的追逐。
考拉茲猜想簡介
考拉茲猜想基於一個非常直觀的叠代過程:
對於任意一個正整數 n,如果 n 是偶數,那麽下一步將 n 除以 2;如果 n 是奇數,則 n 乘以 3 後加 1。重復這一過程,無論起始的 n 是多少,最終總能回到 1。

這個過程並不復雜,算術計算也不復雜,任何人都能理解並親自進行嘗試。以下是 26 和 27 兩個相鄰整數所產生的數列。
初始值為 26 :
26→13→ 40 →20→10→5→16→8→4→2→1
共經過 11 步後歸一,產生的數列中最大數為 40。
初始值為 27 :
27→82→41→124→62→31→94→47→142→71→214→107→322→161→484→242→121→364→182→91→274→137→412→206→103→310→155→466→233→700→350→175→526→263→790→395→1186→593→1780→890→445→1336→668→334→167→502→251→754→377→1132→566→283→850→425→1276→638→319→958→479→1438→719→2158→1079→3238→1619→4858→2429→7288→3644→1822→911→2734→1367→4102→2051→6154→3077→ 9232 →4616→2308→1154→577→1732→866→433→1300→650→325→976→488→244→122→61→184→92→46→23→70→35→106→53→160→80→40→20→10→5→16→8→4→2→1
共經過 112 步後歸一,數列中最大數為 9232。
可以看出,盡管規則簡單,但有的初始值產生的數列卻可能非常復雜。這種簡單的規則帶來的是深刻而復雜的數學問題。
簡單定義下的復雜挑戰
考拉茲猜想的定義雖然簡單,但其背後的不確定性和復雜性令人深思,主要原因在於非線性叠代和缺乏合適的數學工具。
叠代中的非線性計算帶來的復雜
從上面初始值 27 的例子中能夠觀察到,考拉茲過程可能會產生復雜的數列,為什麽會這樣?仔細分析考拉茲過程中的兩個計算:
- 如果 n 是偶數,要執行線性操作 n → n ÷ 2。
- 如果 n 是奇數,而要執行非線性操作 n → 3n + 1。
26 是偶數,27 是奇數。根據考拉茲猜想的規則,偶數和奇數的處理方式不同會導致序列的初始走向完全不同。
再者,對於奇數的「 乘以 3 然後加 1 」是一個非線性操作,因為它涉及到乘法和加法的組合。由此產生的考拉茲序列會展示了非線性叠代行為與一些混沌特性,對初值極其敏感,使得序列的具體行為難以預測。這種不確定性和復雜性構成了證明考拉茲猜想的根本挑戰。
缺乏適用的數學工具
埃爾德什·帕爾在談到考拉茲猜想時說:「數學還沒準備好應對這樣的問題。」傑佛瑞·拉加利亞斯指出,考拉茲猜想「是個異常困難的問題,完全超出了當今數學的範圍」。(維基百科)
目前,數學領域中的經典工具不足以直接解決考拉茲猜想:
探索猜想之路
盡管考拉茲猜想尚未得到正式證明,但大多數數學家仍然相信它是正確的。
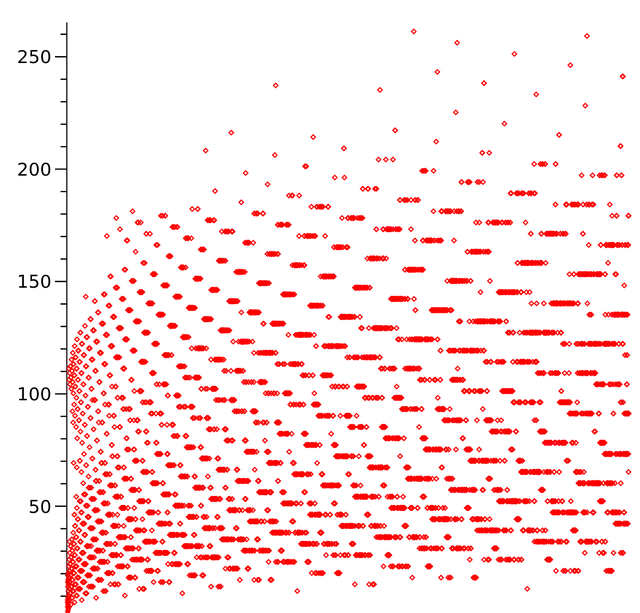
1到9999的數碼及其相應的總停止時間(即歸一的叠代次數)
就這樣,雖然考拉茲猜想尚未得到嚴格的數學證明,但實驗證據和概率啟發式論證都強烈支持是成立的。電腦驗證顯示了海量初始值都滿足猜想,啟發式論證提供了對序列總體趨勢的直覺,數學家的理論工作則進一步鞏固了這些發現,使得大多數數學家相信考拉茲猜想很可能是正確的,但問題依舊懸而未決,許多數學家仍在孜孜不倦地探索。
考拉茲猜想的悖論在於它簡單的定義背後隱藏著極端的復雜性。盡管這一猜想看似簡單,但解開其之謎可能需要數學家在數論、動力系統理論、甚至是電腦科學中找到全新的理論工具。解決考拉茲猜想不僅將是對數論的重大貢獻,也可能在混沌理論、動力學系統等領域產生深遠的影響。
考拉茲猜想的探索之旅提醒我們,數論中看似簡單的問題往往隱藏著意想不到的復雜性和挑戰。對於廣大數學愛好者而言,每一次深入挖掘考拉茲猜想,都是一次對數學深邃之美的探尋。











