當我們深入研究數學猜想時,卡塔蘭猜想就像一個等待破解的誘人謎團一樣吸引著我們。就像一個被一個令人困惑的案件吸引的偵探一樣,我發現自己無法抗拒地被這個有趣的命題所吸引。
該猜想由比利時數學家 Eugène Charles Catalan 於 1844 年首次提出,其神秘性近兩個世紀以來一直吸引著數學家的註意力。其本質在於一個看似簡單的問題:除了 8 和 9 之外,自然數的連續冪對是否只有有限對?
當我思考這個問題時,我被它看似簡單的外表所震驚。乍一看,它似乎很簡單 ——只是探索整數冪之間的關系。然而,在這簡單的外表之下隱藏著一個錯綜復雜的數學關系迷宮,等待我們去揭開。
我對卡塔蘭猜想的深入探究,讓我穿越了質因數分解、模數運算和丟番圖方程式的領域。每走一步,我都會感受到數學推理的優雅和數值模式的優美。
然而,盡管經過了幾個世紀的探索,卡塔蘭猜想仍然懸而未決。它證明了數學的無限復雜性,挑戰我們突破理解的界限,直面數學宇宙核心的奧秘。
當我繼續探索卡塔蘭猜想時,我想起了法國數學家亨利 ·龐加萊的話:「數學就是給不同事物賦予相同名稱的藝術。」
數位的力量
卡塔蘭猜想,又稱米海列斯庫定理,是數論中一個引人入勝的成果。它由數學家尤金 ·察爾斯·卡塔蘭於 1844 年首次提出,一個多世紀以來一直是個有趣的懸而未決的問題,直到 2002 年羅馬尼亞數學家普雷達·米海列斯庫終於解決了它。
卡塔蘭猜想
該猜想涉及強大數學概念之間的迷人交互作用,對於理解某些指數方程式的整數解的結構具有深遠的影響。

考慮大於
1 的整數的平方和立方序列,從整數 4、8、9、16、25、27、32 和 36 開始……
值得註意的是,在這個數列中,兩個連續項不僅是整數的完全冪,而且也是連續的整數。例如,
8(即 2 的立方 23)和 9(即 32,即 3 的平方 32)既是連續的整數,也是整數的冪。
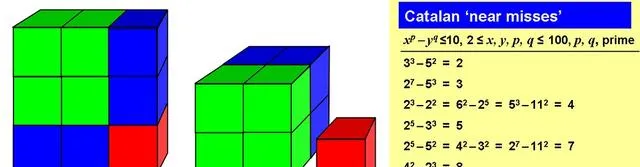
在這裏,我們可以看到對之間的差異增加了。因此,除了對 (8,9) 之外,我們不可能得到等於 1 的差異。
尋求解決方案
卡塔蘭猜想的表述 看似簡單 ——如果「a」和「b」是大於 1 的正整數,並且是互質數(即它們沒有除 1 之外的共同因子),並且它們不是完全平方數,那麽存在等式
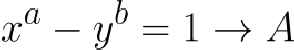
它在正整數 x、y、a 和 b 中只有一個解,即 a = 2 和 b = 3,其中 x = 3 和 y = 2。這意味著除了眾所周知的對 ( ³² — ²³ = 1 ) 之外,沒有其他相差為 1 的連續正整數冪對。
為了解這個方程式,
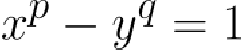
在這裏,因式分解使問題變得容易得多,因為我們現在可以專註於理解 y 的除數。假設 y 是奇數,這意味著 2 不能整除 y。
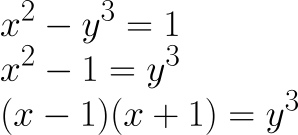
如果
y 為奇數,則 y 的任何因數要麽整除 (x — 1),要麽整除 (x + 1),但不能同時整除兩者。這意味著 (x — 1) 和 (x + 1) 都必須是立方數,因為 y 的所有因數都必須包含在這兩個項之一中。
但是,我們知道兩個立方體之間的距離不可能只有兩個。想想立方體數位的序列 ——1、8、27 等等。每次,我們都在增加更多,對吧?因此,隨著我們沿著這個序列移動,任何兩個連續立方體之間的差異都會越來越大。這就是為什麽你找不到兩個相差兩個單位的立方體。
假設我們有這個方程式。如果 y 是奇數,那麽,結果就是沒有可行的答案。現在,如果 y 是偶數,似乎會給我們一些額外的回旋余地,因為 2 是因數。但是,信不信由你,同樣的想法也適用,在這種情況下你仍然找不到任何解決方案。
Preda Mihăilescu 在數論方面的勝利
這個猜想背後的想法看似簡單,但證明它卻並非易事。它被認為是 21 世紀數論領域的重大裏程碑之一。Preda Mihăilescu 的證明?嗯,他就像是把代數數論中的所有重炮都拿出來了。他深入研究了諸如圓域和伽羅瓦表示之類的東西,相信我,這些都不是輕松就能理解的。他的策略的核心是什麽?他深入研究了所謂的 Wieferich 質數,並使用了伽羅瓦模組結構和模形式理論中一些非常復雜的東西。
為了理解卡塔蘭猜想的特別之處,讓我們回顧一下過去,看看它是如何融入大局的。我們有一位名叫尤金 ·察爾斯·卡塔蘭的人,他是一位來自比利時、擁有法國血統的數學天才。這家夥在數學方面毫不遜色——他在組合學、幾何學和數論等各種領域都引起了轟動。
因此,早在 1844 年,卡塔蘭就給他的數學夥伴約瑟夫·伯特蘭寫了一封信,信中他腦子裏浮現出這個想法。他說:「嘿,如果我丟擲這個大膽的猜測會怎麽樣?」這就是整個事情的開始。
一百多年來,世界各地的數學天才們就像偵探一樣試圖破解這個數學謎題 ——卡塔蘭猜想。他們用盡了書上的所有技巧來證明它是正確的還是錯誤的。在這一過程中,他們取得了一些真正的進展,解決了一些案例,並想出了各種巧妙的方法。但問題是——他們無法把整個謎題拼湊起來。
然後,德國數學大師保羅 ·沃爾夫斯凱爾 (Paul Wolfskehl) 出現了。他對整個加泰隆尼亞猜想非常感興趣,以至於他在遺囑中為任何最終能破解它的人提供了一大筆現金獎勵。現在,盡管沒有人最終獲得該獎項,但它肯定讓每個人都對這個問題感到興奮。沃爾夫斯凱爾的提議點燃了研究人員的熱情,促使他們全力以赴破解密碼。
時間快進到 1985 年——這是卡塔蘭猜想的真正轉折點。想象一下,勞勃·蒂德曼和莫裏斯·米格諾特這兩位數學巫師,各自工作,卻都中了大獎——他們破解了方程式 A 的密碼。他們的發現意義重大——他們證明了,對於任何給定的指數「a」和「b」,這個方程式只有有限數量的解。這就像發現了數學世界中隱藏的寶藏。
現在,他們並沒有完美地揭開卡塔蘭猜想的整個謎團,但這一被稱為蒂德曼 -紮吉爾定理的發現是一個巨大的飛躍。它讓我們得以一窺方程式的內部運作,讓我們走上了更好地理解它的道路。
2002 年,羅馬尼亞數學家 Preda Mihăilescu 取得了突破性進展,證明了該猜想,並借鑒了眾多前輩數學家的貢獻。他的革命性證明發表在題為「基本迴圈單元和 Catalan 猜想的確認」的論文中。
米海列斯庫的方法論融合了幾個關鍵概念和方法論。其中,分圓體理論發揮了核心作用。這些域是透過添加單位根而獲得的有理數體的擴充套件,提供了重要的見解。具體來說,米海列斯庫利用分圓單元的特性和分圓體固有的伽羅瓦模組結構來仔細研究方程式 A。
伽羅瓦模組表示受伽羅瓦群作用的模組。具體而言,它是指具有源自特定域擴充套件的伽羅瓦群的群作用的模組。術語 「伽羅瓦表示」在表示論中通常表示域上的向量空間或環上的自由模組時的伽羅瓦模組。不過,它也可以與「G 模組」互換使用,強調基本代數結構及其與伽羅瓦群作用的交互作用。
Preda Mihăilescu 證明中的 Wieferich 質數和模形式
證明的另一個關鍵部份集中在研究維費瑞希質數上。 Preda Mihailescu 於 2002 年 4 月 18 日完成了他的證明,首先證明除了 (p,q) = (2,3) 對之外,該問題的任何解都必須滿足以下兩個條件:
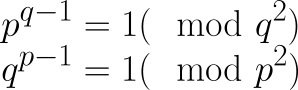
如果質數 p 的平方能被運算式 2^p -1–1 整除,則該質數為維弗裏奇質數。(圖片由作者提供)
P 是以 q 為底的維弗裏奇質數,q 是以 p 為底的維弗裏奇質數。
為了完成證明,米海列斯庫使用了模形式理論的一個深刻結果,具體涉及模形式 Δ(z) — 1,其中 Δ(z) 是判別函式。
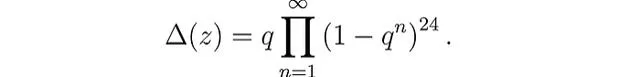
這使他能夠確定,對於
「a」和「b」的特定條件,方程式 A 沒有其他解。
米海列斯庫成功解決了卡塔蘭猜想,贏得了數學家們的廣泛贊譽。他優雅的證明為幾代數學家著迷的問題提供了決定性的解決方案。此外,它還強調了數學界合作努力的有效性。多年來,眾多數學家取得的累積進展為最終證明奠定了基礎,凸顯了集體努力在解決具有挑戰性的數學問題方面的力量。
卡塔蘭猜想的解決不僅解決了一個長期存在的問題,而且還深入了解了特定指數丟番圖方程式的正整數解的底層結構。米海伊列斯庫的證明強調了數位 2 和 3 的重要性,將它們與維費瑞希質數的基本性質及其與模形式 Δ(z) — 1 的關系聯系起來。
此外,米海列斯庫的成就對各個數學領域都具有深遠的影響。它與丟番圖方程式理論、模形式和圓分域探索等不同領域建立了聯系。











