透過前面的學習,我們知道了,定積分可以透過牛頓—萊布尼茲公式問題轉換為線段兩個端點的某個函式差。二重積分可以透過格林公式轉換為積分區域邊界線的曲線積分。三重積分可以透過高斯公式轉換為積分區域邊界面的曲面積分。
今天我們來學習聯系曲線積分和曲面積分的—斯托克公式。
對座標的曲線積分,如果曲線是空間曲線並且封閉,則它可張成一個曲面,可進行對座標的曲面積分。兩者就產生了聯系,而聯系它們的就是斯托克斯公式。
對座標的曲線積分和曲面積分中,曲線和曲面都是有向的。建立曲線積分和曲面積分的關系之前,需要引入右手規則。
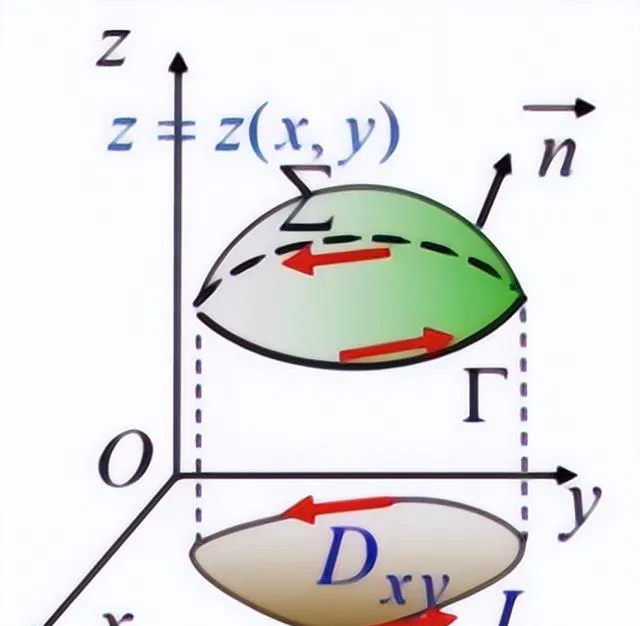
右手規則:設Γ是分段光滑的有向閉曲線,Σ是以Γ為邊界的分片光滑的有向曲面。當右手除拇指外的四指依Γ的方向繞行時,拇指的指向與Σ的法線方向相同,則稱Γ是有向曲面Σ的正向邊界曲線。如下圖:
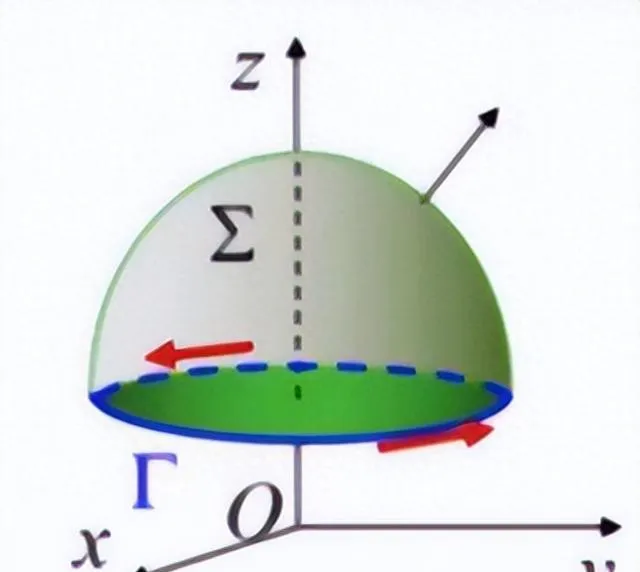
斯托克斯公式:設Γ是分段光滑的有向閉曲線,Σ是以Γ為邊界的分片光滑的有向曲面。Σ的側與Γ的正向符合右手規則,P,Q,R在包含Σ在內的一個空間區域內具有連續一階偏導數,如上圖。則有:
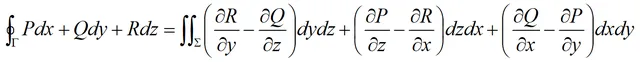
此式稱為斯托克斯公式。
下面給出斯托克斯公式的推導過程:
由於P,Q,R是不相關的,這裏只證明與函式P相關的資訊,其余的可類似證明。
(1)設曲面Σ與平行z軸的直線相交不多於一點,方向取為上側,如上圖。其方程式為:
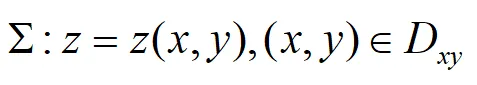
根據兩類曲面積分的關系可得:
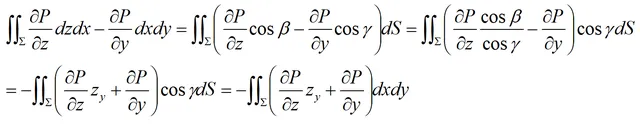
其中:
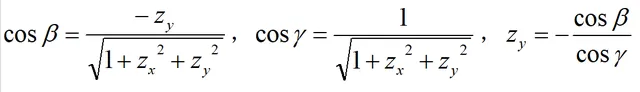
根據一代二投三定向的步驟及多元函式鏈式法則:

再將曲線Γ投影到xoy面為L,如下圖:
根據格林公式可得:

如果Σ取下側,曲線Γ也相應地改成相反方向,上式的兩端同時改變符號,因此上式仍然成立。
(2)進一步地,若曲面Σ與平行於z軸的直線的交點多於一個,則可以添加一些輔助曲線分成幾部份,然後利用前面的公式計算並相加。因為沿輔助曲線而方向相反的兩個曲線積分相延長正好抵消,公式仍然成立。
同理可證其它兩項表示式,因此證得斯托克斯公式成立。
為便於記憶,斯托克斯公式還可記作:
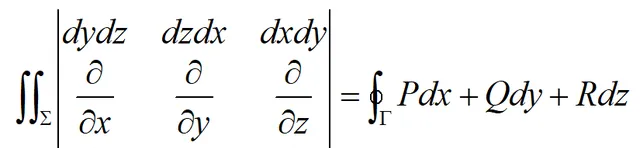
或用第一類曲面積分表示:
特別地,若Σ是xoy面上的一塊平面區域,則斯托克斯公式就是格林公式,故格林公式是它的一個特例。
下面透過一個例子加深理解。求對座標的曲線積分
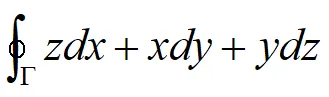
其中曲線Γ為平面x+y+z=1被三座標面所截三角形的整個邊界,方向如圖所示。
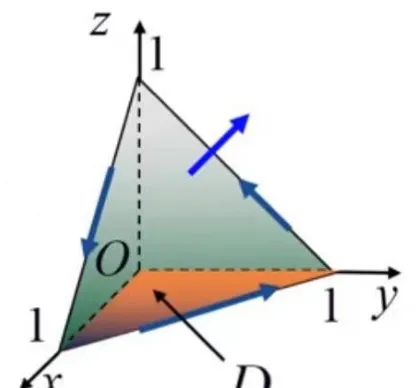
解:記三角形域為Σ,方向取上側。根據斯托克斯公式可得:
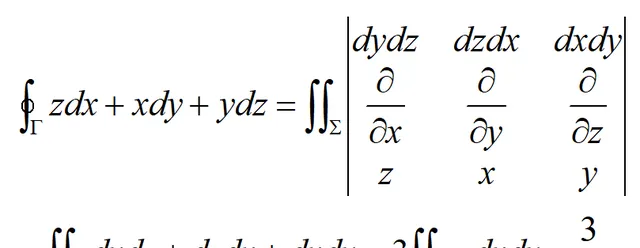
希望本文對你學習斯托克斯公式有所幫助。











