
【數學的邏輯】,[英]鄭樂雋 著,崔凱 譯,中信出版集團2024年3月版。
數學的「規則」來自哪裏
為什麽1+1=2?
對於這個問題,一個可能的回答是:「因為它就是這樣!」它所隱含的意思是:「因為我就是這麽說的!」這是一個讓一代又一代孩子無比沮喪的回答。「因為我就是這麽說的」意味著有那麽一個高高在上的權威人物在制定規則,他可以隨心所欲地使用他的權威而不需要解釋任何理由,其他人必須臣服於這些規則。
由此產生沮喪感其實並不奇怪。實際上,數學所包含的一股強大沖動就是要打破所有的規則,找出這些規則不適用的陰暗場景,以表明所謂的權威人物其實並不像他們想象的那麽有權威。
數學似乎是一個你不得不去遵守的規則世界,難怪它會給人僵化、枯燥之感。相比之下,我對數學的熱愛源於我對打破規則的熱愛,或者至少是對推動規則改變的熱愛。這種行為經常讓我產生一種羞怯感,因為我就像個永遠都長不大的少年。我對數學的熱愛還因為我總是對所有的事情問一個「為什麽」,這更讓我覺得自己就像個長不大的孩子。然而,恰恰是這兩股沖動推動了人類認知的不斷進步,尤其是對數學的理解,它們可以說是數學重要的起源。這一章我們就來談談這個問題。
我想強調一點,在日常生活中我是個奉公守法的人,因為我明白規則代表著群體的凝聚力,是社會安全的重要保障。我相信這些規則,也不介意遵守那些有明確目的性的規則。然而我不相信那些武斷專橫的規則,它們往往沒有正當理由,或者我不相信它們所謂的正當理由。比如,「你必須每天整理好自己的床鋪」(我實在不喜歡做這件事),或者「絕對不要用微波爐融化巧克力」(這的確容易把事情搞糟,但只要你每隔15秒鐘攪拌一次,我發現它是沒有問題的)。

電影【博士的愛情方程式式】(2006)劇照。
所以,我想去探究數學那些顯而易見的「規則」來自哪裏,以及數學這個概念來自哪裏。我會嘗試描述,它如何從一粒種子以自然的過程成長為參天大樹。所謂種子,就是我們每個人,尤其是孩子,經常會提出的那些幼稚的問題,比如為什麽「1+1=2」,而且不會在知道答案之後心滿意足地離開。就像任何植物的種子一樣,它們也需要以正確的方式去培養,需要肥沃的土壤、足夠的空間來伸展它們龐大的根系,當然還需要營養。不幸的是,我們這些幼稚的問題往往沒有以這種方式得到足夠的滋養,而是被貼上「愚蠢」的標簽丟在一旁。在數學研究中,深刻與幼稚問題之間的差別或許就在於不同的滋養方式,也就是說,它們本無差別,都是同樣的種子。
不喜歡數學的人經常被那些明顯帶有專橫意味的結論困擾,即宣稱什麽東西就是正確答案,而沒有任何解釋:「1+1就是等於2!」然而,探究某些結論背後的原因讓我們有機會構建起數學強大的基礎,使其具有清晰的脈絡和縝密的論證過程。有些人覺得清晰性和可靠性令人心神愉悅,其他人則感覺到一種約束感和強迫感。但是類似於「為什麽1+1=2」的問題讓我們有機會發現,數學其實並沒有明確的正確答案,而是在不同的背景下,不同的事情可能是真的。這將引導我們探索數位最初從何而來,算術概念的起源,以及我們如何把這些概念套用到其他數學問題,比如圖形問題上。它涉及數學發展過程中很多重要的主題,從建立事物之間的聯系開始,認真對待抽象的概念,然後一點一點擴充套件我們的思維過程,已涵蓋我們周圍更多的世界。
與其思考「為什麽1+1=2」,我們還不如先深入一步,思考一下這個等式是否在所有條件下都成立。
數學探討的是場景背後的意義
兒童的天性似乎就是喜歡尋找反例。所謂反例,就是證明某件事不正確的真實案例。宣稱某事永遠正確就像為其構築了一道高墻,而尋找與之矛盾的例子就像為推倒這道高墻而付出的努力。這是一種重要的數學學科發展動力。
要想了解孩子們對1+1這個概念的認知,你可以嘗試詢問:「如果我給你一塊蛋糕,再給你一塊蛋糕,那麽現在你有幾塊蛋糕?」但他們有可能會興高采烈地說:「一塊都沒有,因為我把它們都吃掉了。」也有可能會說:「一塊都沒有,因為我不喜歡蛋糕。」
父母們在互聯網上貼出的無忌童言,總讓我覺得興味盎然。我最喜歡的一段對話是,當被問「喬有7個蘋果,他用其中的5個蘋果做了一個蘋果派,他還剩下幾個蘋果」時,我朋友的孩子說:「他已經把蘋果派吃掉了嗎?」我喜歡那些在道理上正確的答案,而不是那些被公認為正確的答案。這是數學非常重要的一個層面,兒童的思維過程往往會揭露一些極為重要卻經常被忽視的數學天性,也就是挑戰不公正權威的天性。
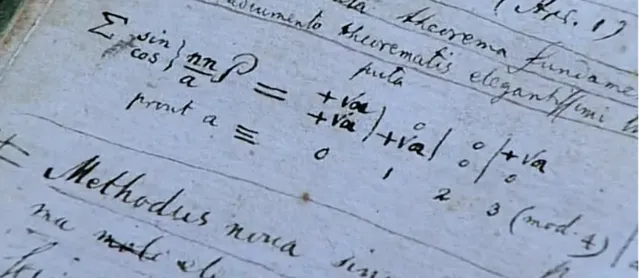
高斯日記原件。紀錄片【數學的故事】(2008)劇照。
孩子們挑戰權威,或許是因為他們有意探索某些事物的邊界,也可能是因為他們想尋找一種自我意識,畢竟這個世界沒有留給他們太多的話語權。我清晰地記得在小時候,遵照大人們的指示做事是多麽令人沮喪。而對某個成年人提出的具有引導性的問題,最有趣的回應方式是將問題的前提一舉推翻,比如我會說我根本不喜歡蛋糕。
從某種程度上說,這樣的回答有點兒惡作劇和破壞性的味道,但我覺得這也算是一種數學的動力。的確,數學或許就是某種惡作劇和破壞性的行為。換一種方式來說,數學就是在探尋事物的邊界,就和孩子們的行為一樣。我們想要搞清楚令某些事物為真的具體邊界,這樣我們就可以確定何時處於「安全」區域,然後在好奇心和勇氣的驅使之下去探索更廣闊的外部世界。這就像一個蹣跚學步的孩子有意跑遠,想看看自己究竟跑到哪裏才能讓大人來追他們。思考1+1不等於2的成立條件就是一個絕佳的例子。
如果我說「我不是不累」,那就是說「我的確很累」。於是有的孩子發明了一個有趣的遊戲,說「我不是不是不是不是不是不是不是不是不是不是不累」,進而變得有些歇斯底裏,因為他們知道誰也記不住他們究竟說了幾次「不是」。這讓我想起了一道令人發狂的數學題,那是一個冗長、煩瑣的計算過程,學生們很容易在負號上犯錯。批改作業的痛苦之處在於,如果學生犯了2次錯誤,或者更糟糕犯了4次錯誤,他們的答案將是正確的。但是在數學的世界裏,答案正確不是唯一的標準,過程也必須正確(下一章我會討論這個問題),所以我不得不仔細檢視每一個計算過程。
另一個讓1+1=0的場景,就是所有的一切都已經是零。就像我小時候的那些糖果:我天生對人工色素過敏,而當時所有的糖果都含有人工色素,所以不管有多少糖果,對我來說都等於零。
有時候,四舍五入的誤差也會導致1+1大於2。如果我們只討論整數,那麽1.4被視為1(最接近的整數),兩個1.4就是2.8,應被視為3(最接近的整數)。所以在四舍五入的世界裏,1+1有可能等於3。一個與此相似但稍有不同的情形是,如果你手裏的錢只夠買一杯咖啡,你的朋友也只帶了夠買一杯咖啡的錢,但把你們倆的錢合起來,或授權以買到第三杯咖啡,因為如果你們每個人手裏的錢是一杯咖啡價格的1.5倍甚至1.9倍,你們就足夠買3杯咖啡了。
有時候1+1大於2與繁殖有關。比如,你把一只公兔子與一只母兔子放在一起,之後你很有可能得到一大群兔子。還有可能是你把相對復雜的事物加在了一起,如果一對網球運動員與另一對網球運動員對壘,那麽不同的排列組合會出現兩對以上的網球運動員。如果第一對是A和B,第二對是C和D,我們就會有以下幾種組合:AB、AC、AD、BC、BD、CD。所以一對網球運動員加另一對網球運動員就等於6對網球運動員。
有時候1+1=1:你把一堆沙子放在另一堆沙子上,結果還是一堆沙子。或者,就像我的一位藝術系學生指出的那樣,如果把一種顏料與另一種顏料混合在一起,你只能得到一種顏色。或者,我曾經看到一個有趣的網路視訊,如果你把一塊義大利千層面放在另一塊上面,它還是一塊義大利千層面(只不過高一些)。

紀錄片【解碼數學】(2011)劇照。
一個稍有不同的1+1=1的場景是,如果你有一張優惠券,買一杯咖啡可以免費得到一個甜甜圈,但每人僅限使用一張優惠券,那麽即使有兩張優惠券,你也只能得到一個甜甜圈(除非你把它送給別人)。或者你在火車上按下「開門」鍵,不管按多少次,效果都與按一次相同。至少它對列車開門的效果是一樣的,但就你可以表達沮喪心情的程度而言可能有所不同,也許這就是為什麽總有人站在那裏不停地按。
現在,你或許覺得以上情形根本不是1+1不等於2的真正原因,因為它們都不是真正意義上的「相加」,或者相加的不是真正的數位,還可能是其他一些牽強附會的原因。你當然可以這樣想,但這並非數學的本質。而數學探討的就是這些場景背後的意義。我們來看看事情按這種趨勢發展的後果是什麽,還有哪些與此類似的情況。讓我們更清楚地了解1+1等於2以及不等於2的條件,這樣我們就能比以前更深入地了解這個世界。
這就是數學的起源。為了探索1+1等於或不等於2的情形,我不希望僅僅去挖掘這個等式的起源,也想一路探究數學的起源。
數學源於人們想要更好地理解事物
數學源於人們想要更好地理解事物。為了更好地理解事物,我們會找到一種更容易的思考方式。一種方法是忽略困難的部份,但更好的方法是秉持這樣一種觀點,即讓我們專註於與我們當前相關的部份,同時不要完全忘記其他部份的存在。
這有點兒像給照相機鏡頭配上一個濾鏡,暫時讓我們關註某一類顏色,之後再換上另一個濾鏡關註其他顏色。或者就像在燉菜的過程中盛出鍋裏的水,讓湯汁變少、變濃稠,當然你不會丟掉這些水,之後還會將其放回鍋裏。
數學最廣為人知的起點是數位。大多數孩子最初接觸數學,或者他們對數學的第一印象是數位,甚至很多人對數學留下的最後的印象也是數位。然而數學不僅僅關乎數位,雖然它呈現出數位的形態,但其實這門學科並不是為了研究數位。更準確地說,它是我們從自己的世界進入數位世界的過程,以及我們在這個過程中的收獲。
數學與數位的緊密聯系在於,對那些喜歡模糊性、創造性、想象力和自由探索的人來說,數位可能顯得很無聊。我不想說數位多麽有趣,恰恰相反,數位的確很無聊,這一點無可辯駁。

紀錄片【解碼數學】(2011)劇照。
然而,數學能包容、整合我們身邊的一部份世界,讓我們盡快從這部份工作中脫身,讓我們富有冒險精神的大腦去探索更令人興奮的那部份世界。這就像利用一台電腦處理生活中枯燥乏味的工作(對我來說包括支付賬單、訂購生活用品、調整食材),讓我可以去做一些更有趣的事情:與人交往、演奏音樂、烹飪可口的食物。
數位源於我們簡化身邊世界的渴望。難怪數學題的答案總是那麽簡單,也總是那麽枯燥。但是我們最初是如何發明數位的,過程卻是相當復雜的。數位源於我們對不同事物之間相似性的探索,以及選擇暫時忽略哪些不同。眼前的兩個蘋果和兩個香蕉讓我們看到了它們之間的某些相似之處,然後我們在大腦中形成「二」的概念。但是為了做到這一點,我們必須忽略蘋果和香蕉作為誘人的水果的具體特征,而把它們當成抽象的、沒有具體特征的事物。這是一次抽象化的飛躍,而且難度很大,孩子們總是需要一段時間來消化這個過程。我們可以適當引導和鼓勵,比如在他們面前反復數數。但他們終究需要憑借自己的力量完成這個飛躍,旁人無法替代。
問題在於,如果忘記了這些事物本來擁有的豐富多彩的特征,只關註那些「讓事情變得更加枯燥」的部份,我們就會讓一切聽起來很無聊。我們不能忘記整件事的初衷,那就是開啟一扇洞悉整個世界的大門。
本文選自【數學的邏輯】,小標題為摘編者所加,非原文所有。已獲得出版社授權刊發。
原文作者/[英]鄭樂雋
摘編/何也
編輯/張進
導語校對/柳寶慶











