中国古代数学几何从诞生,就是围绕着「用」——测算天道之「用」在发展。
从【周髀算经】,一直到清代江永的【数学】、杜知耕的【几何论约】、黄百家的【勾股矩测解原】……;从勾股定律到矩阵、弧矢推算,从刘徽的割圆术到祖冲之的缀术……无不是为天道推算而服务的。
而天道推算的结果呢?在文字不够发达的上古,总是以图象——八卦的形式在陈述。
这就意味着数理化天赋不高者,是学不精易学的。
为什么呢?
因为除了易历推算不给力,就光平面、曲面与空间之间的翻转,就能让数理化天赋不高者翻的晕头转向。
因为中国的数学几何作为易历推演的工具,她和西方传统数学几何是不同的。
西方传统的数学几何是平面几何,也叫欧氏几何。
而中国数学几何从萌芽,就是空间几何,曲面几何,属于非欧几何。
所以在学习易学的过程,关于平面、曲面和空间的翻转能力至关重要!
为什么呢?
咱们先看一下欧氏几何和非欧几何的区别
如果我们把眼睛当成微分器,欧氏几何都是被眼睛微分后的平面几何学,就像我们上古时代的地平坐标,都是受视野限制下的认知。
而欧氏的两条平行线永不相交论,正是视野局限下的公理。
也就是说,欧氏的两条平行线,之所以平,之所以直,之所以不相交,都是源于我们视野的局限。
如果我们站在整个宇宙视野里,看欧氏在地球上画的那两条平行线,其实都是附在地球面上的曲线。
如果这时候,我们再回到地球平面上看,随着视野的差小,欧氏的两条线,又变成了两条永不相交的直线。
正是这个原因,时过数千年,走到黎曼时代,西方几何学围绕着视野问题,发生了一次变革。
也就是说,黎曼面对欧氏的两条线,做了一次视野和视角的转换,从欧氏的地平面转向了宇宙,于是欧氏的两条平行线,就变成的地球的两条经线,得出:平行相交论。
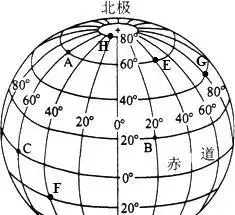
就这么简单,黎曼就得出了平行线相交论,开创了非欧几何。(附论:黎曼在曲面上提出这一论点时,忽略了一个问题,那就是和纬线平行的线,无论在曲面上如何空间化,都是是符合欧氏不相交论的 。 )
我为什么要讲这段西方几何的历史变革呢?
因为中国数学几何从诞生,研究对象都是天道——曲线、曲面和空间。
也就是说,因为中国数学几何从诞生就是空间几何,是围绕着曲线、曲面在发展的非欧几何。
所以,作为天文历算图像表达的八卦,刚一入门就考验着初学者从平面到曲面、从曲面到空间的翻转能力。
这个能力是学易的天赋基础!
比如我昨天讲的:阴阳太极图就是七衡六间平面图的空间圆图,可就是最基本的一翻,让很多读者都翻迷了,纷纷留言表示质疑。
为什么呢?就是这些读者缺失学易的天赋基础,缺失从空间到平面、从平面到空间互相转换的基本能力。
再比如勾股定律,勾股定理其实就是把太阳的周天圆运动的黄经度(八卦的圆图),利用圭影的长短以及直角三角形,进行了平面化的推演。如果连这一点最基础的内容都翻不过来,如何学国学呢?
也就说,围绕着天道推演为中心的中国文化,不是文科,而是理科,所以我并不建议数理化天赋不高者学易、学医,因为光空间、曲面、曲线、直线和平面之间的翻转,就能把你翻到晕头转向。











