考拉兹猜想(又称为奇偶归一猜想、3n+1猜想)是一个深刻的数学未解难题,以其简单直观的定义和证明上的巨大挑战吸引了无数数学爱好者和专业数学家的追逐。
考拉兹猜想简介
考拉兹猜想基于一个非常直观的迭代过程:
对于任意一个正整数 n,如果 n 是偶数,那么下一步将 n 除以 2;如果 n 是奇数,则 n 乘以 3 后加 1。重复这一过程,无论起始的 n 是多少,最终总能回到 1。

这个过程并不复杂,算术计算也不复杂,任何人都能理解并亲自进行尝试。以下是 26 和 27 两个相邻整数所产生的数列。
初始值为 26 :
26→13→ 40 →20→10→5→16→8→4→2→1
共经过 11 步后归一,产生的数列中最大数为 40。
初始值为 27 :
27→82→41→124→62→31→94→47→142→71→214→107→322→161→484→242→121→364→182→91→274→137→412→206→103→310→155→466→233→700→350→175→526→263→790→395→1186→593→1780→890→445→1336→668→334→167→502→251→754→377→1132→566→283→850→425→1276→638→319→958→479→1438→719→2158→1079→3238→1619→4858→2429→7288→3644→1822→911→2734→1367→4102→2051→6154→3077→ 9232 →4616→2308→1154→577→1732→866→433→1300→650→325→976→488→244→122→61→184→92→46→23→70→35→106→53→160→80→40→20→10→5→16→8→4→2→1
共经过 112 步后归一,数列中最大数为 9232。
可以看出,尽管规则简单,但有的初始值产生的数列却可能非常复杂。这种简单的规则带来的是深刻而复杂的数学问题。
简单定义下的复杂挑战
考拉兹猜想的定义虽然简单,但其背后的不确定性和复杂性令人深思,主要原因在于非线性迭代和缺乏合适的数学工具。
迭代中的非线性计算带来的复杂
从上面初始值 27 的例子中能够观察到,考拉兹过程可能会产生复杂的数列,为什么会这样?仔细分析考拉兹过程中的两个计算:
- 如果 n 是偶数,要执行线性操作 n → n ÷ 2。
- 如果 n 是奇数,而要执行非线性操作 n → 3n + 1。
26 是偶数,27 是奇数。根据考拉兹猜想的规则,偶数和奇数的处理方式不同会导致序列的初始走向完全不同。
再者,对于奇数的「 乘以 3 然后加 1 」是一个非线性操作,因为它涉及到乘法和加法的组合。由此产生的考拉兹序列会展示了非线性迭代行为与一些混沌特性,对初值极其敏感,使得序列的具体行为难以预测。这种不确定性和复杂性构成了证明考拉兹猜想的根本挑战。
缺乏适用的数学工具
埃尔德什·帕尔在谈到考拉兹猜想时说:「数学还没准备好应对这样的问题。」杰佛瑞·拉加里亚斯指出,考拉兹猜想「是个异常困难的问题,完全超出了当今数学的范围」。(维基百科)
目前,数学领域中的经典工具不足以直接解决考拉兹猜想:
探索猜想之路
尽管考拉兹猜想尚未得到正式证明,但大多数数学家仍然相信它是正确的。
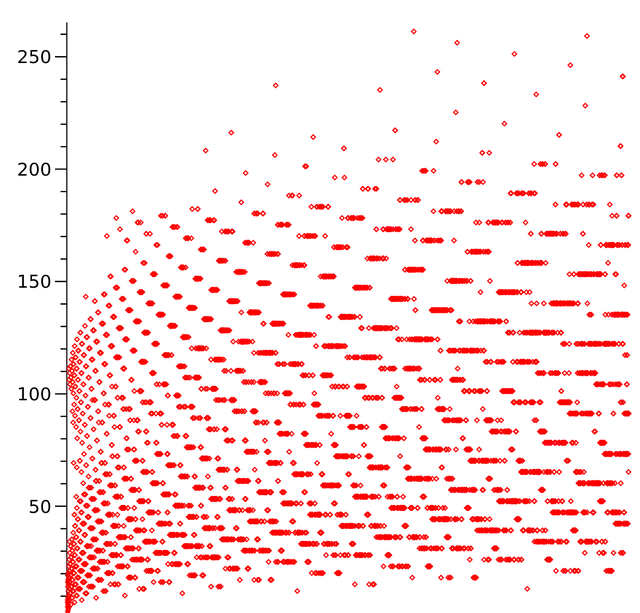
1到9999的数字及其相应的总停止时间(即归一的迭代次数)
就这样,虽然考拉兹猜想尚未得到严格的数学证明,但实验证据和概率启发式论证都强烈支持是成立的。计算机验证显示了海量初始值都满足猜想,启发式论证提供了对序列总体趋势的直觉,数学家的理论工作则进一步巩固了这些发现,使得大多数数学家相信考拉兹猜想很可能是正确的,但问题依旧悬而未决,许多数学家仍在孜孜不倦地探索。
考拉兹猜想的悖论在于它简单的定义背后隐藏着极端的复杂性。尽管这一猜想看似简单,但解开其之谜可能需要数学家在数论、动力系统理论、甚至是计算机科学中找到全新的理论工具。解决考拉兹猜想不仅将是对数论的重大贡献,也可能在混沌理论、动力学系统等领域产生深远的影响。
考拉兹猜想的探索之旅提醒我们,数论中看似简单的问题往往隐藏着意想不到的复杂性和挑战。对于广大数学爱好者而言,每一次深入挖掘考拉兹猜想,都是一次对数学深邃之美的探寻。











