
扭结(绳结)理论(knot theory) 不是仅仅关于鞋带和领结的领域,它是一个对纯数学的发展和现代世界的进步至关重要的领域。有几项发现彼此紧密相连,没有这些发现,扭结理论是不可能存在的。绳结可以追溯到几个世纪前,但它们在当时没有任何数学意义。
首先,什么是绳结? 凯尔特结 (celtic knots)是一些最早广泛使用的绳结,遍布整个凯尔特文化。
它们是没有起点或终点的环,历史学家认为它们可能象征着永恒或自然界中生命的无尽循环。另外还有一种就是中国结,它们承载着祝福、幸福、繁荣、爱情等意义。但这些都是文化上的东西,现在让我们进入真正的内容,即绳结的数学研究。
那么,如何开始从数学角度研究绳结呢?在成为数学领域之前,绳结只是我们用于绑扎物品、船只、钓鱼、衣物等实用的东西。我们第一次看到绳结作为数学对象出现是在亚历山大·狄奥菲勒·范德蒙的1771年著作【位置问题的评论(Remarks on Problems of Position)】中。
范德蒙对线条或点的交织或排列感兴趣。他想象了一个场景,其中有三根绳子,每根绳子的两端分别连接到两个柱子上。范德蒙的研究兴趣在于这些绳子在交织或编织时,如何在保持其整体结构不变的情况下进行扭曲或重组。这意味着在研究过程中,绳子不能被切断或解开。

我们不知道是什么促使他提出这个问题,但当时类似的问题如欧拉对柯尼斯堡七桥问题的解决方案也是一种趋势。
那么这一研究是如何在100年后被重新提起的呢?卡尔·弗里德里希·高斯提出了 连接数(linking number) 的概念,用于测量两个封闭曲线或环在三维空间中如何交织。想象一下有两个环A和B,
如果它们没有接触或交叉,连接数为零,因为它们完全独立,没有任何连接。现在把环B提起并通过环A的中心一次,从上方通过并从下方出来,然后再环回到顶部 ,在这种情况下,连接数是+1或-1,如何确定哪个呢?

在继续之前,我估计绝大多数人并不理解上面蓝色字体所表达的意思(或操作过程),疑惑的点在于「环是否可以切断? 」,答案是可以的,操作也非常简单:把B环从某处扯断,形成一根绳子,绳子从A环穿过一次,在把绳两端拼接起来。

我们继续,如何确定连接数是+1,还是-1?首先,为每个环确定一个方向,比如总是顺时针或总是逆时针。

如果从你的角度看顶部环从右到左交叉底部环,那么这就是正交叉;如果从左到右交叉,这是负交叉。因为环B从环A下方通过并从左到右出现,这是负交叉或-1。

总连接数是这些交叉点的计算总和,所以如果有几个交叉点,就将它们加起来得到最终的数字。

高斯研究这个问题的动机是什么呢?高斯在研究积分时引入了连接数,测量两个封闭曲线如何在空间中相互影响。
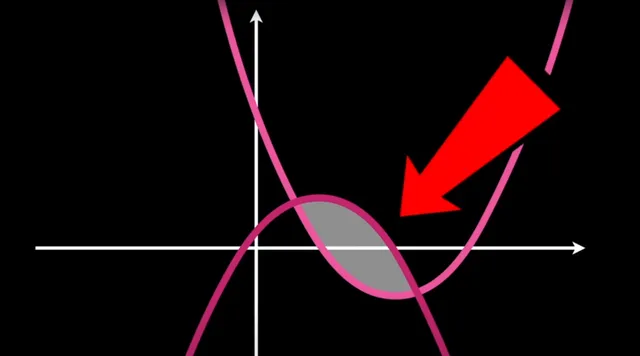
它成为拓扑学和绳结理论的基本内容。
那么,什么时候我们开始将这个领域称为扭结(绳结)理论的呢?
有几件事情发生了。首先, 流体动力学 (fluid dynamics)和 涡流行为 (vortex behaviors)成为了主流,
赫尔曼·冯·亥姆霍兹在这方面做出了重要贡献,这些理论又影响了威廉·汤姆森(开尔文勋爵),他提出原子可以被建模为以太中的结涡管。
结涡管(knotted vortex tubes)是一种在流体力学和物理学中出现的概念,主要涉及涡旋在流体中形成复杂且闭合的绳结状结构。涡旋通常是流体中的一个旋转区域,而当这些旋转的流体形成闭合的环状结构时,它们可以呈现出类似数学绳结的形状。

显然,现在我们知道这是错误的,但当时它启发了绳结理论之父,彼得·格思里·泰特(Peter Guthrie Tait)。泰特在托马斯·彭宁顿·柯克曼(Thomas Penyngton Kirkman)的影响下,首先系统地分类和编制了绳结,

并在1877年发表的【爱丁堡皇家学会会刊】中将其作为一个独立的数学学科。因此,他创建了第一个全面的绳结表,这些表格基于绳结的属性和复杂性进行分类。他使用了诸如计算最少交叉点数的方法来区分不同的绳结。泰特的工作包括提出了 泰特猜想(Tait's Conjectures) ,
泰特猜想主要涉及图论中的图嵌入和结理论,以下是几个著名的Tait猜想:
四面体图猜想(Four Color Theorem): Tait最早提出的猜想之一,他猜测在平面图中使用四种颜色可以使得每个相邻的区域具有不同的颜色。这个猜想后来在1976年由Kenneth Appel和Wolfgang Haken通过计算机辅助证明被解决。
交替结猜想(Tait's Conjecture on Alternating Knots): Tait猜测任何一个交替结的镜像具有相同的交替表示。这一猜想在20世纪20年代由Kurt Reidemeister证明。
从根本上说,泰特是第一个将绳结理论作为一个独立的数学学科进行分类的人。
当然,开尔文的理论被否定了,因为我们发现原子并不是这样的,但对绳结理论的数学研究仍然在独立地发展。詹姆斯·克拉克·麦克斯韦进一步扩展了泰特的「绳结表」,但接下来的一大进步是库尔特·赖德迈斯特在1926年提出了 赖德迈斯特移动 (Reidemeister moves),这成了绳结理论研究的基石。
赖德迈斯特移动非常重要, 因为它们提供了一种方法来确定两个绳结图是否表示相同的绳结。 如果你可以通过只使用这些移动并多次应用,将一个图转换为另一个,那么这两个图就被认为表示相同的绳结。
赖德迈斯特确定了三种基本操作(移动),这些操作可以应用于绳结图:

想象一下取一小段绳子,将其扭曲成一个环,使得绳子在某处交叉,一部分在另一部分的上方或下方。


本质上,需要取两条平行的线段,要么通过将一条拉过另一条来将它们分开,要么使它们靠拢,以便一条跨过另一条。

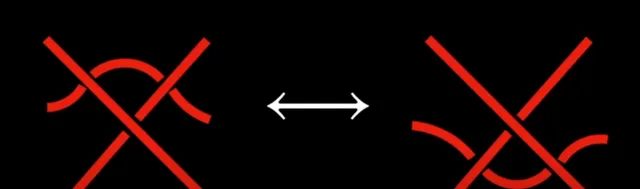
本质上,需要将绳结的一部分滑过由另外两部分形成的交叉点或X点。
为什么我们需要这些操作呢?赖德迈斯特移动很强大,因为它们允许数学家在不改变绳结实际结构的情况下探索绳结的基本属性。 通过应用这些移动,我们可以简化或改变绳结图的外观,同时保持绳结的重要属性,这对分析和分类绳结至关重要。
还有一种称为 绳结不变量(Knot Invariants) 的发展,有着相同的目的。赖德迈斯特移动和绳结不变量通过不同的方法分析绳结的属性,并发挥不同的作用。
詹姆斯·亚历山大在1923年引入了 亚历山大多项式 (Alexander Polynomial),让我们以 三叶结(Trifoil knot) 为例,
这是最简单的 非平凡绳结 ,因为它不能在不切割的情况下被解成一个简单的环 。亚历山大多项式有助于将三叶结与简单绳结如简单环和其他更复杂的绳结区分开来。因此,如果有两个绳结,它们的亚历山大多项式不同,那么它们不是同一个绳结。简单环的亚历山大多项式是1,即Δ(t) = 1,而三叶结的多项式是
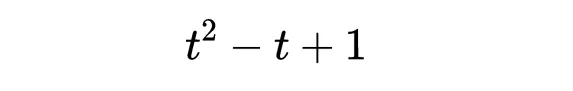
这证实了三叶结确实是一个非平凡结。
亚历山大多项式是对称的,当你用1/t代替t,
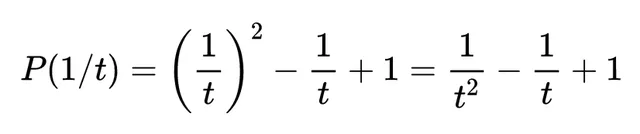
然后乘以多项式的最高次项t^2,
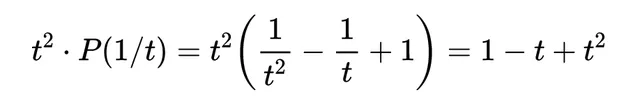
这表明三叶结是 手性对称的 ,具有一种特定的对称性。所以,它们用于研究和理解绳结的深层属性,超越了它们的视觉表示。
1984年,沃恩·琼斯引入了 琼斯多项式 (Jones Polynomial),这是一个强大的突破。它是一种绳结不变量,类似于亚历山大多项式,但能够捕捉到绳结和链条的更细微特征。沃恩·琼斯在研究冯·诺伊曼代数时发展了琼斯多项式,这完全是数学的另一个领域,但它最终对绳结理论具有突破性意义。
它是如何发展的呢?琼斯多项式涉及分析绳结图或绳结的绘制方式。第一步是看绳结的图,特别是关注交叉点,绳结的一部分与另一部分交叉的地方。对于绳结图中的每个交叉点,应用某些规则,可以改变交叉或考虑线条可能通过或在彼此下方的不同方式。每个不同的排列或状态分别考虑。每个状态都赋予一个代数表达式,这个表达式取决于交叉的方向,即线条是在上方还是在下方。
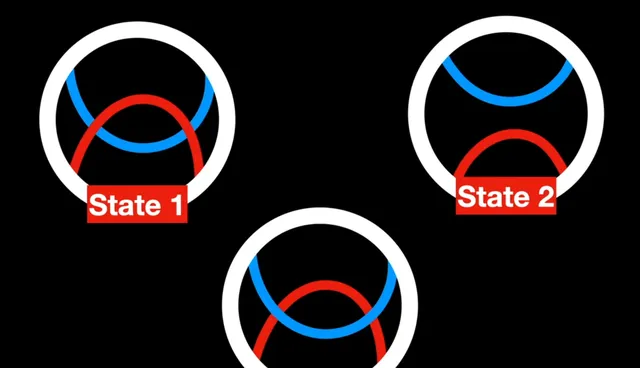
最终的琼斯多项式是通过组合这些状态的代数表达式得到的,
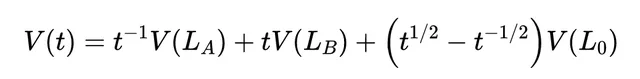
它与拓扑学的发展是如何联系但又独立的呢?一个很好的例子是 双曲绳结理论(Hyperbolic Knot Theory) ,这是一个结合拓扑学、几何学和群论的领域,主要归功于威廉·瑟斯顿在1970年代和1980年代的工作。在瑟斯顿的工作之前,绳结理论主要研究三维空间中的绳结和链条。然而,瑟斯顿引入了通过双曲几何理解大多数绳结和流形的概念 。
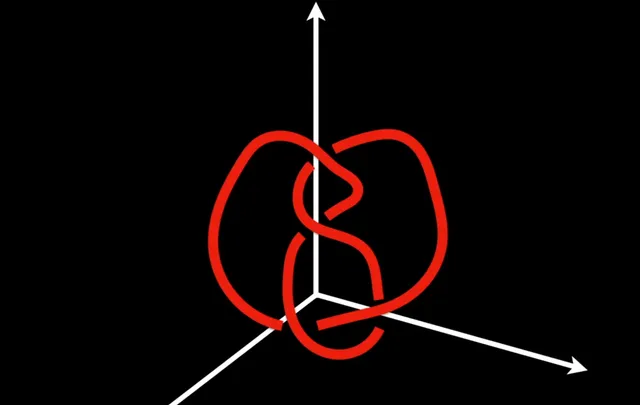
如果一个绳结的周围空间适合应用双曲几何,即该空间可以定义为具有恒定的负曲率,那么这样的绳结称为双曲绳结,其周围空间因此形成一个双曲流形。
这些绳结限于三维空间,是否发展到其他领域呢? 虚绳结 (Virtual Knots)由路易斯·考夫曼在1999年引入,这是一个非常重要的发展,因为它允许在传统三维空间之外探索绳结。虚绳结的一个关键特征是它们包括虚交叉,这些不是实际的交叉,而是指示在更复杂的表面上可能发生的交叉。这些是在绳结图中标记的不同于经典交叉的交叉点,它们不代表一个上下关系,而是表示在没有额外背景的平面中无法表示的交叉信息。
事情还没有结束, 科万诺夫同调 (Khovanov Homology)在2000年由米哈伊尔·科万诺夫引入,这扩展了琼斯多项式的概念,提供了关于绳结的更丰富信息。它涉及构建一个与绳结图相关的链复形,
每个链图中的链接贡献一个分级模,一个数学结构,这些模通过微分链接。通过应用同调代数技术,包括链复形的同调,科万诺夫提取出分类琼斯多项式的不变量。科万诺夫同调将绳结理论与代数几何、范畴论和同调代数等其他数学领域联系起来。
扭结理论作为数学、物理学、化学和生物学等多个学科的交汇点,为这些领域之间提供了共同的语言和工具。例如,扭结理论在理解量子场论中的拓扑缺陷、DNA分子的结构变化以及化学中分子结合的动态中起着核心作用。











