光子密码(一):电磁波的物理行为
(一文洞悉光的秘密)
光明无所不在。
却又深藏人类智慧之眼的凝视中如坠黑暗。
我们未曾一睹光的真颜,仅仅模糊察觉出,光是一根纽带。
联结物质,能量和场。
探讨光明本源的学说如浩瀚大海,但是,很少能够直观揭示
光,到底是,什么?
光子是物质,还是能量?是波,还是粒子?又有着怎样的空间结构和行为?
它从何处来?又要到哪里去?
关于光子的终极秘密,是否只能深藏宇宙深处。
或者,她就在身边,只是我们恍若未觉。
这是一篇宏文,但在漫长的穿行之后,您一定会觉得不虚此行。
因为您会发现,我们原来可以与光明的真身如此接近。
一 论述的理论依据
1.能量守恒
我们关于能量的认知最直观的来源于力所做的功。当然,我们现在知道力的本质实际上是不同属性场之间的相互作用,而其效应便是吸引或者排斥。
通常的结果导致作用对象的位置改变,而这种位置的连续改变,正是我们熟悉的物体速度的来源。在力的作用终结之后,物体会保持位移的速度。
而一个具有质量的运动物体,是我们对于能量最直观的认识。
最直觉的现象则是物体或环境的温度,如果我们承认温度的本质实际上也是粒子的运动速度的外在表现,则我们上述的两种表述实际上具有同样的物理内涵。
如果这种做功的结果不是转换为物体的速度,而是逆着场的方向将物体移动到一个特定的位置。一旦我们撤销作用力,则居于该位置的物体会在场的原有作用下推动物体发生位移,最终转换为物体的运动。
这个因为在场中特定位置所具有的推动物体运动的趋势,我们称之为势能。
显然,动能和势能,正是我们最容易理解的两种能量形式。
可见,能量的本质是场相互作用必然导致的属性不同的两种效应,一种是呈现为速度的动能,一种是具有转换为动能趋势的势能。
而无论动能还是势能,产生的根源均是场相互作用。
所以, 能量的本质就是场相互作用必然导致的效应,这种效应作用于对象物体,可以呈现为势能和动能两种具体形式。
我们同时知道,外力做功导致的速度,在外力撤销后会保持不变。
这种我们称之为惯性的运动物体普遍的物理属性,实际上隐含着一种宇宙间最基本的规则之一,那就是能量守恒。
速度不变代表的动能不变,意味着在没有外界干扰下,一个特定的速度和物体对应的动能不会改变。
完整的能量守恒表述为, 在一个孤立的系统内,能量既不会凭空产生,也不会凭空消失,他只能从一个物体传递到另一个物体,从一种形式转为另一种形式。
能量守恒作为一种观察规律,一旦普遍存在,就成为我们考察某个对象时,被考察对象必须遵循的一个基本规律。
我们对光子的考察,也正是基于这一宇宙间最基本的规律之一。
在光子中,时变电磁场的能量转换遵循这一规律,而光子,在我们将场作为基本的物质范畴的前提下,本身并不是能量,而只是能量转移的一种形式。
2.物质守恒
能量守恒无论怎么看,好像都属于宇宙间最基本的规则之一,但是,我们认为,在能量守恒的表面,暗藏的是更基本的物质守恒。
我们已经说过,能量归根结底,不过是场相互作用的一种效应。
场相互作用,显然决定于场的基本属性。我们从场相互作用的两种基本表现考察这种基本属性。
在电磁场中,同种场表现为场线方向上的排斥,用外力令拥有同种场的两个带电体在场线方向上靠近,撤销外力后,他们会自动离开,恢复带电体各自的位置或者原本具有的速度。这种和弹簧类似的性质,可以顺理成章的让我们得出场具有弹性。
引力出现在异种场的场线方向上,效应是带电体会自动靠近。
看起来就像是带电体之间的场消失了,但更像是卷曲,因为在我们分开吸在一起的异种带电体后,带电体各自的场依然存在。
无论是消融还是卷曲,现在最流行的解释是真空场,即异种场必然湮灭在真空中,而从真空中可以产生异种等量的异种场。
但无论哪一种解释,都不影响我们将要得出的结论,即
宇宙中,场的矢量和保持不变。
于是,被外力或带电体自身的初速度不为零的碰撞导致的拥有同种场的带电体,在外力撤销或碰撞结束后,一定会恢复原来的状态;防止在作用力范畴的拥有异种场的带电体必然会靠在一起,彼此的场消融从而失去带电性质。
而物质场表现出异种电磁场的特性,无差别存在于所有的物体。
如果我们合理认定通常意义的物质实际上不过是场的一种凝结态,则场守恒现象可以推广到所有的物体。
于是进一步推导出物质守恒和电荷守恒就是水到渠成的事情。
因此,能量本身和能量守恒,归根到底属于物质守恒的一种延伸现象。
能量作为一种场基本属性决定的相互作用效应,在物质矢量守恒的基础上表现为守恒现象。
物质守恒显而易见的单否点在于导致引力效应的物质场没有像电磁场那样的对称场。
这有两种合理的解释。
其一为携带物质场的所有物体本质上就是物质场的对称场;
其二为物质场的总量本身就是不为零的一个负值。
3.光子的波动理论
我们在进行光的空间结构、能量转换转移以及位移机制的描述中,均遵循光子是一种波的俗成理论。
在真空中,麦克斯韦电磁方程组可以推导出如下的形式
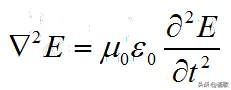
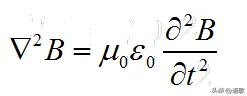
方程与普通物质波的波动方程相似,
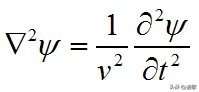
物理学规律表明,如果两种事物运动的函数形式一致,那么它们必然属于同一类物理行为。
也就是说,时变的电磁场是一种波。
于是,我们以光子必须服从波的一般规律,作为考察光子各种属性的基本准则。
然后在以波动现象为基础,导出光的粒子形态为某个时刻的差别仅仅在于空间尺寸大小的同一波结构。
4.最小能量单元原理
宇宙中存在几个基本的最小能量单元。
这与普朗克常数相类似,但在我们的描述中,这个最小的能量单元并不等于这个数值,而且普朗克常数也并非我们设定最小能量单元的依据。
我们关于最小能量单元的设想,在于我们对磁场或电场强度的计算时,通常会采取线积分、面积分和体积分的形式。
而积分的最小微分单元,可以合理设定为一条电场力线、磁力线甚至引力线。
我们对最小能量单元的设定,正好就是一条上述力线携带的能量,而且我们认为,时变电磁场中,无运动电荷那样的实物依托的时变电场和时变磁场,均遵循这个最小的能量单元。
我们对光子或电磁波空间结构的描述,也正好是这个表现为单一电场力线和磁力线的最小能量单元,并且在关于光子能量的相关阐述中,我们会进一步阐述这个最小能量单元,然后试着去证实它属于一个常量。
及所有的电磁波和光子,携带的能量均为这个最小的能量单元。
您会不假思索想到的普朗克量子能量公式,看起来会轻易判定上述原理的荒谬性,但是,这个您所认为的能量,在我们的描述中只是属于一个能量密度。
我们所设定的最小能量单元,与这个普朗克能量计算结果直接相关,但并不相等。
这样,我们就可以认为,所有电磁波谱中,电磁波表现的空间尺寸的差别,根本原因在于能量密度的差别,能量密度越大,光子半径越小。
一 时变电磁场的空间形态
1.时变电磁场中磁场的空间形态
电场和磁场是两种客观存在的事物。这看起来的确属于无需质疑的基本事实。
而佐证这一点的恰恰是我们正在试图考察的光子。因为光子的本质笼统而言,正是藕联存在的时变的电磁场,更重要的一点在于,脱离了光源之后,光子仍能继续存在。
这充分证明场并不是那种我们为了描述某种非直接相互接触的物体间的相互作用而引入的纯数学量。
电流必然伴随磁场,并且磁场垂直于电流方向,以电流为中心呈同心圆分布,电流与磁场方向的关系遵从右手定则。
这属于一种观察事实。

而且磁场强度与电流强度的关系如下

当然,对于我们考察的光子或电磁波,更有意义的是运动电荷的电场和磁场,因为我们认为,离开光源之后的光子,缺乏运动带电体那样的实物依托,遵从一个最小的能量单元。
运动电荷周围存在磁场,这显然很容易理解,因为我们会理所当然的把直线电流和多个电荷的直线运动等同起来,而事实也正好如此。
但是对于运动电荷,普通人往往更关注运动,而把运动电荷的电场忽略掉。

(单个运动电荷的磁场,以及磁场方向和电荷运动方向的相互关系)
实际上,单个的运动电荷不仅存在电流伴随的那种磁场,更拥有自己的电场。运动电荷的电场强度如下所示
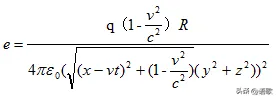
为了方便比较,我们自然需要同时给出静止电荷的电场强度如下

静止点电荷的电势为

而运动电荷产生的磁场为
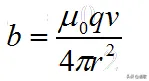
不难看出,运动电荷电磁场的关系为
对于以上的看起来或简或繁但直观上差别明显的公式,我们在此给出的唯一意义在于,我们试图表明我们将要给出的一些推定,确实存在相应的理论依据,并不是纯粹的异想天开。
通过上面几个形式上一目了然的公式,我们可以确定,点电荷从静止转为运动后,电场强度以及与电场能量直接相关的电势均发生了明显的变化。
这个变化,无疑正是磁场产生的原因
如果从能量守恒和物质守恒的角度进行考察,我们可以认为,
电荷的运动导致了电场的变化,在能量和物质守恒规则的约束下,
磁场正是是运动电荷相对于静止电荷,电场的变量。
或者说, 磁场的本质是运动电荷相对于静止电荷的电场能量的变量。
至于磁场到底是运动电荷运动方向上的变量,或者其它方向的变量,亦或兼而有之,我们不得而知。
只是从电场总是与运动电荷垂直这种性质来看,似乎与运动方向的变量具有更密切的关系,因为这意味着两种场不发生相互作用(垂直的电场无相互作用)。
这个变量的大小显然取决于电荷的运动速度。
当速度不变亦即电荷匀速运动时,得到的是恒定的磁场;如果速度为零,则磁场消失;如果速度是变化的,必然导致变化的磁场。
磁力线总是表现为以电荷为中心的闭合曲线,而在点电荷周围,这种曲线呈现为正圆,这自然是由于点电荷在平面上具有各向同性。
同时,点电荷的各向同性决定的不仅仅是磁场的形态,也包括磁场的强度。即正圆闭合曲线上,磁场强度处处相等,因此磁场中不存在电场那样由不同位置决定的强度差。

磁场具有明确的方向,与电荷运动的方向服从右手定则。
磁场因为具有方向,而且磁场的基本性质决定磁场可以对磁场内的小磁铁做功,但是功是一种矢量,如果把功与能量等同起来,则磁场总功的矢量和显然为零。
这意味着磁场对外界缺乏做功的能力,显然,这是磁场只能改变电荷运动方向的内在根源。
如果我们合理忽略的磁场做功矢量特征,则推动小磁铁绕行磁力线一圈,磁场仍然可以得到一个确定的不为零的量值。
而这个量值,我们亲切的称之为 磁场的内禀能量 。
假如进一步结合变化磁场能够产生感生电动势,以及磁场的本质是运动电荷电场或场能变量的观点,那么,在能量守恒基本规则下,我们可以合理推定,磁场的内禀能量,正好是电场能量的变量。
磁场的本质就可以视为一种电场能量变量的载体,承载运动电荷电场变化的变量,并通过自身的变化把内禀能量重新还原为电场能量。
如果我们把电荷的运动和与运动电荷匹配的电场进行等效处理,则我们可以合理推测变化电场与伴生磁场的空间关系描述如下

在上图中,磁力线表现为以电力线为中心的同心圆。
至于运动点电荷周围的磁场是圆面还是圆形环线,这一点很难观察并证实。
已知的电磁学实验证实不同磁性物质周围存在不同的磁场,图示如下
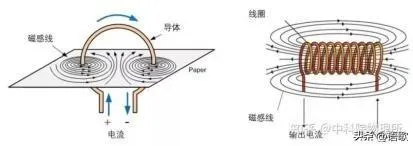


显然,以上图示无论如何都不会让我们得出磁场是单一正圆曲线的结论。
但同样不可否认,磁场线呈现为上述诸图中类似于平面的原因,在于导线或中引发磁场的是很多电荷,并且并不是所有的电荷的运动方向都完美一致。
因此,我们可以认为,直线电流或磁体中存在不同的垂直于电流方向上的电荷电场变量的分量。各个分量的矢量和呈现不同数值,因此对应不同的磁力线,从而使通电直导线周围的磁力线呈现为不同半径的同心圆。
如果我们考察的是一个最小的能量单元,比如单一磁力线对应的能量。
则单一电场线对应的磁力线必然是闭合的正圆线。
在变化的电场中,因为变化仅仅改变磁场的大小,所以,时变电磁场中磁场的空间形态就同样是上述的匀速变化电场的伴随磁场模式。
于是, 对于一个最小的能量单元,时变电磁场中,磁场的空间形态就呈现为以作为磁场源的电场为中心,垂直于电场,方向遵循右手定则的正圆闭弦。

2.时变电场的空间形态
基本的电磁学实验揭示,条形磁铁插入环形导线能观察到环形电流。
由于电流和电场必然在同一个方向,我们似乎可以轻易得出磁通量变化产生的磁场是以磁铁为中心的正圆环线。如下图所示

不过,闭合的电场自然可以通过这种方式产生,但我们可以同样合理的认为,磁体插入其它非正圆形状的线圈也必然会观察到非圆形的电流。
同时,另一种产生感生电流的方式,即闭合回路导线切割磁力线同样可以产生电流,而闭合回路显然可以呈现为不同的空间形状。
因此,上述两种产生感生电流的方式本质上是一样的,都表现为闭合回路对磁力线的切割运动。
同时,感生电流产生的是电动势,而电动势与电场并非两个完全一致的事物。
所以,单单考察感生电流现象,我们不足以令人信服的描绘出时变电场具体的空间形态。
于是我们不得不转而通过闭合电路对时变电场进行考察,好在真实的物理世界,变化的闭合回路和带电粒子的变速运动,是产生时变电磁场的主要方式。闭合回路中电场的形态和变化方式,反而与时变电磁场中的电场更加一脉相承。
显然任何通电闭合回路均可以改造为下述的正方形。
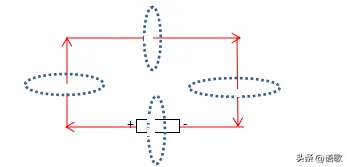
在上述回路中,由于电流处处相等,平行回路必定产生方向相反强度相等的磁场,而根据基础的电磁学实验,它们之间的存在大小相同的排斥力。
显然,在排斥力作用下,导线具有向外运动的趋势。如果我们同时假定导线可以无阻力改变自身位置,那么,相同的力就以正方形回路的中心,造就了导线在受力方面的各向同性。
于是最终的结果,就是导线呈现为以正方形中心为圆心的正圆。
如果我们进一步调整电流的大小,使得导线之间刚好没有作用力。
这样,所有的磁场线必然刚好穿过正圆回路的圆心。 如下图所示

如果断开电路,理想导线电流消失,导线周围的磁场随之消失。然而由于电源的存在,正圆导线中,仍然存在一个正圆的电场。

如果将电源换成不可见的电场,上述结构自然同样成立。所以,我们可以合理推定,一个强度确定的电源,必然匹配一个半径确定的正圆非闭合电场。
和磁力线类似,真实的电源的电场线与上述的模式差异显著,如下图所示
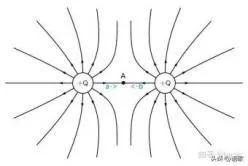
不过采用与前述磁力线同样的考察方法,我们可以得出,时变电磁场中,时变电场的空间形态,呈现为一个正圆非闭合开弦,电场的源位于磁场未闭合处。源外电场的方向和源内相反,但都表现为从正到负。
电场中,电场强度从正到负逐渐降低。

这种不闭合的时变电场的空间形态模型,与电磁力学描述的时变电场为闭合曲线完全不同,但这并不应该成为您立即否定我们的观点的理由。
因为完全闭合曲线必定使电场线与磁力线拥有同样的性质,因此会推导出时变电场对外做功的矢量和为零的必然结果。
但这显然是严重背离事实的。
另外,电场的源在电场线上,因此不具备磁力线那样源在中心的各向同性,电场强度在电场线上不是处处相同,而是沿着一个确定的方向逐步减低。
如果我们保留时变电场的非闭合特性,那么这种能量分布不均匀特征,使得电场具有了非对称导致的极性。
时变电场的极性表现为,时变电场产生的磁场,只能位于能量集中的电场线未闭合处。
这种极性,正是电磁波在真空中单向传播而非双向传播的根本原因。
3.时变电磁场的空间形态
我们已经给出时变电磁场中,时变电场和时变磁场的空间形态。
但是,这并不意味着继续给出时变电磁场的空间形态是可以一蹴而就的事情,因为电磁感应中,电场感生磁场和磁场感生电场产生的电磁藕联体,其空间形态大相径庭。
相比之下,我们更容易得到电场感生磁场是电磁藕联体的空间结构,因为磁场的本质就表明,它只能以变化的电场为源,且以电场为中心。
这样,设定一个最小能量单元的闭合电场,则时变电场感生磁场的空间形态可以描述如下图
简略的描述就是,时变电场与电场产生的磁场呈现为彼此垂直,相互穿过圆心的正圆套环,由于电场非闭合导致的极性,感生磁场只能位于电场的非闭合侧。
至于时变电磁场中,变化磁场产生的感生电场的电磁藕联体,通过对感生电流的进一步考察,可以发现他们不能做简单的相互替换。
基本物理学实验揭示的产生感生电流的方式包括如下两种,
其一为感生电流,特指磁场强度变化感应生成的电流;
其二为动生电流,特指闭合回路导线进行切割磁力线运动感应生成的电流。
如果我们把磁场强度与磁通量进行等效处理,则上述的感生电流和动生电流并无本质的区别,因为它们都表现为闭合回路内,磁通量的变化。
无论哪种感生电流实验,均表现为闭合回路中观察到电流的存在,而回路导线切割磁力线显然更容易为我们判断电磁的相对位置提供直观依据
我们通常认为,所有以动生方式导致感生电流产生的直接原因,在于闭合回路导线中,导线内的电荷与磁力线的相对运动,导致运动电荷受到磁场的偏转作用,引起电荷在导线被移动,最终形成电流。
这样,在动生电流中,电流的产生就只能在导线切割磁力线时,而电流的位置,必然位于磁力线上。
于是,动生电流实验中,与动生电流等效的电场,就必然位于磁力线上。
因此在最小能量单元条件下,时变电磁场中,时变磁场产生电场时,电磁藕联体就只能呈现为如下的形式
简略的描述是,在时变电磁场中,时变磁场感生的电场与磁场相互垂直,且具有相同的圆心。
行笔至此,我们实际上只是给出了时变电磁场中,电磁感应及磁电感应各自的空间形态,至于在时变电磁场中,上述两种空间形态如何联结在一起,我们只有在进一步考察了时变电磁场中的能量转换和转移机制后,才能最终呈现。
二 时变电磁场中的能量的转换
为了更顺畅的进行我们将要进行的关于时变电磁场中的能量转换问题,我们需要先考察能量和场的关系。
我们在文章伊始,已提到过能量和场,也指出物理学对能量的基本定义是对物体做功大小的一种度量,同时指出,场相互作用是力的内在根源。并且在场守恒规则下,场具有的压缩和消融不得不在外界因素撤销后回归原本的状态,而场的这种属性,无疑正是能量的唯一来源。
由于场具备对处于场中且携带同类场的物体通过场的相互作用导致物体位移的能力,我们可以认为,场虽然是一种客观存在的物质,但具有能量属性。
或者说,场具有能量。
这种能量包括同类场相互作用的位置改变和位移,相应的对应势能和动能。
场和能量的这种内在同一性意味着场和能量能够进行相互转换。
另外,我们在开篇也已经指出,时变的电磁场是一种波。因此 必然存在与普通物质波相似的一般特征。
只需对物质波进行简单的考察,不难发现在所有正弦变化的物质波中,存在动能和势能的周期转换。
这种转换由介质的自身属性决定,这种介质属性决定的能量转换的必然性,是物质波表现为周期运动的内在根源。
在物质波中,以水波和琴弦的振动为例,势能表现为某个时刻介质的位置,而动能表现为介质的运动速度。如果忽略物质波的双向传播和介质自身相互作用对能量的损耗,则对于波构成的正弦曲线的任一点,势能和动能绝对值的和均为一恒定值。
也就是说,在我们设定的上述条件下,物质波遵循能量守恒。
同时需要指出,如果我们并不知道介质的物理属性,那么,我们能够观察到的波的外在表现,只能表现为位置的连续变化。换句话说,我们能观察到动能,但是我们观察不到势能。势能仅仅存在于洞悉介质属性的思维之中。
也就是说,介质在势能转换的过程中,速度增加的根源在于势能的存在,势能是动能增加的原因。这一点单纯依靠眼睛,是无法直接看到的。
势能不能独立存在,因而不能独立呈现。
作为物质波的一种基本特征,光子或电磁波的能量转换形式,在麦克斯韦方程组中有明确的表述。
我们先来考察磁感应电现象。
麦克斯韦电磁方程组给出的感生电场方程如下
方程对于缺乏高等数学知识的多数人来说不太容易理解,但是一旦转换为下述的形式就会一目了然
该式正是法拉第感生电流方程,式中ε为感生电动势,Φ为磁通量,t为时间。方程的通俗解释就是,磁通量的变化可以产生感生电动势,其大小为磁通量的变化率。
对法拉第电磁感应定律做数学处理,可以得到感生电场的麦克斯韦电磁方程(步骤从略),但是经处理后得到的不再是磁通量与时间的变化,而是感生电场与变化磁场的相互关系。
继续对感生电场方程进行处理,可得到电场的波动方程(从略)
由于该方程符合波动方程的一般形式,因此它可以描述为正弦函数曲线。
但是感生电流感生的并不是电场,而是感生电动势,这属于能量的一种形式。
如果对感生电动势与时间关系作图,则可得到电动势与时间的余弦函数曲线(具体推导从略)
显然,因为上述的两种曲线均由法拉第电磁感应电流推导而来,上述两种曲线是变化磁场感生电场的两种不同表达方式,表达的是同一现象中的不同能量形式感生电动势和电场强度的变化规律,
于是,完整表述两种能量函数的关系图就是
上图表明,在磁场最弱(0点处)的0π处,磁场强度的变化率最大,感生电动势最大;而在磁场最强的π/2处,磁场强度的变化率最小,感生电动势最小。感生电场中,电动势和电场存在π/2的相差。
因此,在单独审查时变电磁场的以电场呈现的示意图中,我们看到的,就不能再是单独的电场,而是在电场强度变化曲线的任一点,同时暗含一个电动势,场的绝对值和势的绝对值之和为一固定值。
通过前面的描述,我们大致清楚在时变电磁场中,磁感生电虽然呈现为电场强度的正弦变化,但是正弦变化曲线的任一处,电场均伴随直接感知不到的电动势。
于是,我们将用感生电场代替上面的普通电场,同时通过上述的曲线,一目了然的揭示出,时变电磁场中,时变电场以感生电场的方式存在。
感生电场的周期变化中,伴随感生电动势的相差π/2的周期性变化。
进一步与普通的物质波进行简单的比较,可以发现,时变电磁波中,时变电场的能量转换形式就是作为势能的电动势和感生电场能的一种相互转换。
如果一定要把时变电场作为一种物质,则电动势和感生电场的相互周期性转换,就可以视为能量和物质的相互周期性转换。
我们可以用类似的方式进行时变电场产生时变磁场的感生磁场的考察。
在真空中的麦克斯韦电场方程组中,描述上述变化的方程式如下*(为了方便比较,同时给出感生电动势公式)
与感生电场不同的是,这个方程来源于安培环路定理
另外,B与E的大小不同,其相互关系为
除此之外,感生磁场与感生电场遵循一样的变化规律,且可以进一步推导,感生磁场与感生电场相互垂直且同相变化(具体推导步骤从略)
于是,我们便得到时变电磁场中能量转化的形式如下:
- 时变电磁场中,能量转换表现为电磁场势能与电磁场强度或场能的周期性变化,这种变化具有必然性,是时变电磁场以波动形式传播的内在根源;
- 在电磁场各自周期转换的函数曲线中,任一点的电磁场强度和电磁势的绝对值之后是一个固定值,或者说在转换周期中存在能量守恒。
- 光子或电磁波在传播途径中遵循能量守恒的基本因素,与光子或者电磁在传播路径上的单向传播一齐,共同决定光子或电磁波在传播路径上不衰减。 (均可以通过数学证明,此处从略)。
对时变电磁场强度周期性变化规律在形式上与物质波动方程的一般形式进行代换,可得到时变电磁场中,电场和磁场均以固定速度传播
显而易见,既然是根据波动方程一般形式进行的速度代入,那么,时变电磁场中,电波和磁波的速度的定义就应该同时满足波动方程中对速度的一般规定,
即 时变电磁场中,电波和磁波的速度相对于光源。
因为电波进而磁波的速度均为真空磁导率和真空介电常数决定的常量,所以,这同时表明任何能量的电波和磁波,均具有相同的传播速度。
如果我们把一个周期内电波和磁波的传播理解为电场和磁场在空间中以同心圆状扩散,则可以推定,任何强度或能量的电波或磁波,均以相同速度扩散,这个速度本身是电波和磁波在空间中传播的内在根源。
显然,这种同一周期内电场和磁场的变化规律,并未表明电场和磁场必然存在像水波或琴弦那样的空间起伏。
波动的只是电场和磁场的强度,而不是路径的起伏。
行笔至此,好像所有的描述均已尘埃落定,但是事实远非如此。因为迄今为止,所有的描述均局限于某一个周期和相应的空间内,电磁场的相互关系。
即使已经推算出时变电磁场中,时变电场和时变磁场的扩散速度,但是,也并不表明这种同一周期内的电场和磁场行为,就必然超出一个周期的范畴。
而一个周期内,势能和动能呈现正弦周期性变换,以及空间行为的周期性变化,均不足以确定某种事物的能量波动,能够远离源或者超出一个周期的空间范畴,而向周期外的空间传播。
一个司空见惯的实例便是一个压缩的弹簧,放开压缩后同样可以表现为弹簧势能和动能的正弦样周期变化,但是这种周期变化仅仅局限在特定的位置,而缺乏传播行为。
因此,单单从麦克斯韦电磁方程组,不足以确定时变电磁场能够以波动方式传播。所以,我们必须进一步考察时变电磁场中,藕联电磁场的位移和能量转移
三 时变电磁场的能量转移和位移
在一个可传播的波动形式中,能量转移和位移实际上具有相似的内涵。
我们以更直观的水波的能量转移和位移机制来说明这一点。
水波的实物形态表现为下图
表明在水介质中,起源于某处的能量变化,由于介质的各向同性,以波源为中心,向周围平面呈同心圆状扩布。
我们看到的波纹幅度逐渐减小,在于在传播路径上环形波对应的扩散半径在增大,同时,水波介质属性决定的在特定方向上的双向传播和介质相互作用对能量的损耗,均致使水波在传播过程中逐步衰减。
如果我们只做一个长方体的水槽,并限制槽的宽度足够小,然后阻止水波的双向传递,同时忽略介质相互作用对能量的损耗,那么,我们就可以得到一个传播实际空间形态和正弦曲线非常接近的图示
如上图所示,水波在曲线上某点均存在一个水平的分量和垂直方向上的分量,水平分量是位移的原因,而垂直方向上的分量导致波峰处的重力势能和波谷处的压强势能的相互转换。
通过介质的相互作用和重力作用,处于a点的势,就被转移到a /处,同时我们说,一个势的位移,和水波的传播,实际上指代的是完全一致的水波的空间行为。
时变电磁场如果能够超越单一周期的空间范畴,就必须具备像水波位移那样的能量转移机制。
在此之前,我们已经得出电生磁与磁生电的相互关系图示
但是直接将它们耦合起来,并不能令人信服。
为此,我们需要考察正副电路实验,该实验虽然本质上属于感生电流实验,但显然更有利于在此处佐证我们将要表达的时变电磁场的位移机制。
下面是一个正副电路的示意图
图示左侧是一个由开关控制电流的主电路,右侧是带电流计的副电路,实验的文字描述是:在开关合拢的瞬间,副电路中能检测到方向相反的电流;而在开关断开的瞬间,副电路检测到同向电流。
至于产生这一现象的原因,正是由于正电路中,随着开关合拢,产生一个突然出现的电流,而根据电磁基本规律,伴随电流必然存在一个突然出现的磁场。
这个突然出现的磁场,正是副电路中检测到反向电流的原因。
更重要的一点,副电路中的b,与正电路中的a,在空间上并不重叠,并且,同样处于副电路且距a更远的c点,仍能检测到反向电流,差别仅仅是其强度较b点弱。
所以通过正副电路实验,我们可以得出这么一个结论,即通过磁场的介导,一个电流的变化被转移到空间的另一个位置。
如果将电流的变化转换为电场的变化,根据电场变化与磁变化的必然联系,我们可以得到类似的结果,而副电路感生的,属于电动势而不是单纯的电场。
差别仅仅在于,突然出现电流等同于电场的突然消失。
如果我们把上述的变化与电磁波产生的如下方式做比较
不难看出,正反电路的突然断开和突然合拢,如果控制变化的速度为正弦改变,则正副电路实验实际上可以等同于电磁波产生方式的半个周期变化。
因此,我们拥有充分理由,可以把时变电场中,变化磁场介导的感生电动势位移机制,认定为时变电磁场中,电动势的位移机制,而电动势的位移机制,无疑正好是电磁波的位移。
结合前述的电生磁和磁生电论述,我们可以推定以下的结论;
1.时变电磁场中,变化的电场引起变化的磁场,而磁场以电场为中心,在空间同一平面呈同心圆以速度c扩布;
2.时变电磁场中,变化的磁场感生电动势,且位于磁力线上,随着磁场的空间扩布,新的电动势从变化的源电场转移到扩展磁场的边缘;
3.源电场消失后,感生电动势形成新的源,在此重复上述的周期性变化;
4.时变电磁场中,传递或转移的能量,是外界因素导致的电场的变量,整个转移的过程中,这个变量保持不变。
然后,我们给出时变电磁场中,任一时刻电磁场藕联和空间相互关系如下
这将是令人振奋的一个图,因为它展示了 单个电磁波或者光子最接近物理真实的空间图像为三联体结构。
为了这个新生的事物能被广泛接受,我们需要对其进行进一步的阐释。
- 能量-时间密度和能量-长度密度
为了正确理解电磁场的空间扩布,我们需要对能量和能量密度进行考察。
我们首先考察能量时间密度,一个简单而实用的例子为登山
我们给出上述两种不同模式的登山示意图,左图为以一种不同的速度等同一座山峰;右图则表示以不同的长度登上同一座高度相同的山峰。
我们用这两种方式考察能量-时间密度和能量-长度密度
显然在第一种方式中,速度越快,登山者花费的时间越少,但是会感觉越是吃力,如果以劳累的感觉作为个体做功或者说耗费能量大小的一种度量,则
在第二种登山方式中,速度相同,但是路径不等,因为登的是同一座山峰,这样,路径越短,单位距离耗费的能量越大,我们反而越吃力;而路径越长,单位距离耗费的能量越小,我们会觉得更轻松。
而与我们的考察目标更接近的是水波的传播
如果我们设定水波在传播路径上单向传播,且忽略水分子相互作用对能量的损耗,则水波在传播在传播的过程中,随着距波源的距离越大,每一个波的能量密度减小,波幅减小,但波的总能量均等于波源处的能量。
于是我们感知到的某列水波的能量,实际上是一种能量长度密度。
如果设定一个最小的能量-长度密度单元eρ,且任一点A距源的距离为r,则任一列水波的总能量
于是,对于一个具体能量而言,我们通常指代的是能量密度,包括能量时间密度和能量-长度密度。如果能量越大,能量长度密度越小,;能量越小,能量长度密度越小。
因此,一个越小的能量,必定对应一个更大的长度;而越大的能量,对应一个越小的长度。
同时,由于时间与速度导致的长度呈正相关,因此
一个特定的能量-时间密度,必定匹配一个适宜的能量-长度密。
2.时变电磁场的空间扩布
在阐述时变电磁场的空间扩布之前,我们需要提到一个重要的物理定律,
即 任何一种能量,总是趋向于自更高的能量密度向更低的能量密度扩散;同样,可扩散的物质也总是趋向于从密度更高的地方扩散,这个过程是不可逆的。
如果我们承认上述的扩散定律是正确的,那么,电磁波和光子中,时变电场和时变磁场的空间扩布就非常容易理解,因为
时变电场和时变磁场的空间行为,本质上是一种能量和物质 (此处我们认定场为物质的一种形式) 的扩散。
结合时变磁场其中一种半个周期的强度-时间曲线
上图中,左为磁场强度与时间关系,右为磁场空间位置与周期中特定时间关系
完整的描述就是,0-π/2周期遵从能量扩散规律,磁场势能从最大值逐步转化为磁场,势能从一个半径为零的空间逐步扩散,直到π/2时刻,势能全部转换为磁场。
π/2-π周期遵从物质的扩散规律,磁场从最大值逐步转换为磁势能,磁场自一个强度最大的空间,随着强度变小,半径逐步增大,直到π时刻,磁场全部转化为磁势能。
因此,整个周期,在能量和物质扩散规律的制约下,磁场从半径为0的电场或电流源,以一定的速度扩布到π时刻,然后磁场消失的瞬间,磁势能达到最大值。
因为磁场的空间变化和电场的空间变化一致,因此可以通过完全一致的方式推导出电场的空间变化。
差别在于,电场的源在电场线上,而磁场的源为中心的电场。
由于时变电磁场中,时变电场和时变磁场属于同一个最小的能量单元,因此,电场在空间上表现为以移动的磁力线为圆心,因此,电场在空间的位移与磁场相反。
可见,时变电磁场电感应磁中,电场空间扩布方向与电磁波或光子的传播方向相反,而磁场扩布方向与传播方向相同。
因此,时变电磁场中, 感生磁场的空间扩布构成电磁波或光子空间传播的唯一要素 。
而在磁感应电中,时变电场和时变磁场同样遵循一个最小的能量单元,虽然电场的源位于电场线,但因为两者的半径相同,空间上表现为时变电场和时变磁场以共同的圆心在空间同步扩布,两者始终为半径相等相互垂直的套环。
上述电磁场的能量和物质扩布的速度的界定,电磁动力学有明确的界定推导,且时变电磁场的能量速度和不同强度电磁场的空间扩布速度均为
由以上可知,单纯考察时变电磁场的同相变化,我们只能描绘出在一个周期的时间和空间范围内,时变电场和时变磁场存在能量的周期性正弦变化,以及时变电场和磁场的空间恒速扩布,并不能充分阐明电磁波或光子超出一个空间的范畴,在更广泛的空间传播。
3.时变电磁场在自由空间的传播
通过上面的描述,我们已经知道,只有把电感应磁与磁感应电这两种在空间行为上差别巨大的的电磁互感现象综合起来,我们才能得出时变电磁场在自由空间传播的真实规律和具体空间行为。
首先必须确定,由于磁场不能脱离变化的电场独立存在,因此,在可传播的时变电磁场中,波源归根结底为时变的电场。
在时变电磁场中,时变电场感生磁场,通过磁场的空间扩布,致使时变电磁场具备了空间传播的可能性,这种扩布在半个周期末达到空间的最大值。这便是电磁波的位移机制;
在时变电磁场中,源处感生磁场的变化通过磁电感应生成感生电动势,感生电动势位于在空间中扩布的磁力线上。
在半个周期末,感生电动势达到最大值,并随感生磁场的空间范围最大,一个与源电动势大小相同,方向相反的新的电动势,就从源电场的空间位置,移动到远离源电场的另一个空间位置,这便是电磁波的能量转移机制。
在源电场和源电场感生磁场消失的瞬间,一个新的与源电场位置不重叠的源得以出现,并采用与源电场相同的形式,引发又一个电磁波的产生。
所以,在可进行空间传播的电磁波中,感生磁场的空间扩布构成位移基础,而感生电场构成能量转移和空间传播机制,显然,磁场的空间扩布速度,因此在数值上等于电磁波的空间传播速度。
而在自由空间中,电磁波之所以沿直线传播,则服从能量最低原理的支配,即在无外来能量干预下,可传播的事物将沿最短路径及直线传播。
这样,我们就终于走到了一个激动人心的时刻,因为我们具备足够的条件,可以描绘出传播路径上,电磁波和光子的空间行为了。
为了能够一目了然,我们仍然采用半个周期的方式,通过给出0、π/2和π三个特殊时刻电磁场的空间结构,最简化的描绘出电磁波的空间行为图示,为读者想象出一个连续的电磁波的空间行为制定三个最关键的参数
0时刻 :此时刻电磁波的空间结构为一个尺寸无限接近零的点,在这个点,存在一个最大的感生电动势,而且电场和感生磁场即将出现,并具有最大的变化率,我们用一个紫色的粗点来描计这个特殊的事物
π/2时刻: 此时刻,电动势和磁势经由能量扩散规律的支配,完全转化为电场和磁场,以0时刻的源为中心,磁场在空间中扩布到传播方向上的1/4λ的距离,电场的扩布方向相反;同时,同相变化的感生电场也达到最大值,电场的极性部位与感生磁场的边缘重叠于1/4λ处
π时刻: 此时刻,电动势和磁势经由物质扩散规律的支配,在空间中达到最大范围1/2λ,并即将消失。感生电场完全转换为感生电动势(紫色方框),感生电场、源电场及源电动势(黑边方框)均即将消失,感生电动势达到最大值(紫色方框),与源电动势反向,且和感生磁场的最大边缘边缘重叠于1/2λ处。
如果我们以π周期为单位考察两个临近的电磁波,则可得到下述图像
所以,电磁波和光子在传播路径上呈现为三联体结构,至于为什么不是现有电磁波形态图例描述的如下四联体结构,即随时变电场的感生磁场的感生电场中,并不同时产生感生磁场
原因有二,其一,电磁波同普通物质波一样,本质上是一个固定能量的空间转移,这个固定能量作为源电场中场的变量,也是电磁波的最小能量单元,是电磁波产生的阈值。在能量完全转换为与源同质的电动势之前,新的能量转移低于这个阈值而不足以发生。
其二,如果继发的感生电动势再次产生感生磁场,则因为所有电磁场均表现为同相变化,这必然导致电磁波的无限数量感生和无限速度传播,这与我们观察的电磁波不衰减传播且有限速度传播完全不一致。
因此,电磁波只能是三联体结构,而不可能是四联体结构。
4.最小能量单元
我们多次提到一个最小能量单元,现在我们已经具备最充分的条件对其进行阐述。
我们之所以会假定一个最小能量单元,显然并非仅仅因为异想天开,而在于一个实体(比如电荷或导线电流)产生的电磁场,因为实体自身的空间特性(各向同性或非各向同性),产生的电场在空间中呈现多种不同的形态,并且因此拥有不同数量和形状的磁力线或电场线。
而在时变电磁场中,这种电荷或者电流的实体并不存在,因此,通常的电场线或磁力线形态就不能作为时变电磁场中,磁力线和电场线的形态依据。
同时,我们通过考察电磁波谱,并结合对电磁波能量的现有理论值其实极小,因此进一步假定存在一个最小的能量单元。
在这个最小的能量单元中,只存在一条电场线或磁力线,而且电场的能量和磁场的内禀能量相同,均等于这个最小的能量单元。
现在,我们尝试推算出这个最小的能量单元。
以电磁波中的磁场为例,在π/2时刻,磁势完全转换为磁场,因此,此时刻磁场的内禀能量就等于我们正在考察的能量单元
显然,为了计算出这个闭合圆环的总能量,我们有两种方法,其一为能够计算出某点的磁场力,然后乘以周长。显然在此处并不适用,因为这需要计算出磁场的强度和设置点磁体的大小。
另一种方法是在知道某点能量,及能量-长度密度的基础上,应用这个密度去乘以磁场线的周长。
当然,能量-长度密度我们仍然无法给定,但是,根据我们前述对能量时间密度与能量长度密度的相互匹配,我们认为,可以用一个能量时间密度代替这个能量-长度密度。
当然,这样的处理显得有些牵强。
但是我们先搁置这个小小的纰漏。
我们回过头去看磁场的空间扩布,我们曾经指出,在磁场自0点向周围扩布中,半径增大同时周长增大,但在能量守恒原则下,每个周长的总能量保持不变。我们感知到的不同周长的磁场的能量差异,就像扩散的水波一样,实际上是能量密度在减小。
因此,我们通常意义上的能量,实际上指代的是能量密度。
而在我们考察电磁波能量时,通常以与扩散半径直接相关的波长相匹配的周期大小作为能量的度量,即能量公式为
这是著名的普朗克能量公式,当然其中h为普朗克常数,而v为电磁波频率
因此,我们可以合理认为,上述普朗克能量公式进行计算的,实际上是电磁波的能量密度。所有的电磁波的总能量实际上是不变的,频率越大,周期的时间越长,磁场以相同速度扩布的半径越大周长越长,因而电磁波的能量密度越小。反之,则频率越大,电磁波周长越小,能量越大。
按照这种推理,我们就可以计算磁场或电场最大的π/2时刻,电场或磁场(内禀能量)的总能量(两者相等)
在π/2时刻,对应的电场或磁场半径均为1/4λ,因此,按照能量密度乘以周长,可得
转换一下就是
又因为光速的另一种计算方式为波长乘以频率,
所以,最终的能量单元公式为
上式中,π、h和c均为常数,所以,这个常数就是所有电磁波共同的能量单元
任何电磁波与波空间尺寸匹配的能量密度可以不同,尺寸越小能量越大,但总能量是在保持不变。
我们可以进一步粗略计算其值
e=0.5×3.14×2.99×108×6.62×10-34=3.1×10-25
这个计算值与电子磁矩的测定值9.28×10-24非常接近,而电子磁矩接近我们对最小能量单元的规定。
因此,我们对最小能量单元的设定和值的大小的计算就不至于太过异想天开。
最小能量单元的意义在于,它作为源电场变化的最小变量,决定了可传播电磁波的阈值,在非匀速变化电场中,只要变化量达到或超出这个阈值,这个变量就不会重新蜕变为电场,而将以波的形式在空间中传播。
四 电磁波和光子的源依赖性
我们已经提到,电磁波归根结底来源于磁场的变化,磁场与电流密切相关,而电流的空间位置受到导线的直接影响.
因此,实际的电磁波可以呈现不同甚至大相径庭的空间形态,甚至可以随着源的旋转等运动而不断动态变化。
我们并非对电磁波所有的形态感兴趣,上面也只是按最简单的形式进行考察,以便给出一种最容易理解的电磁波空间行为模式。
我们需要进一步考察的只是源处电磁波的空间行为及源周期运动产生的电磁波和振动粒子产生的电磁波,因为它们具有一定的特殊性。
1.源处的电磁波或光子
源的特殊性在于,源处的电磁波是双向传播的,这显然与我们前述的电磁波在传播路径上的单向传播不同。
在我们的描述中,但光子或电磁波具有极性,但是这种极性只存在于传播方向,在与传播方向垂直的两侧,但光子存在左右对称。
于是,源处电磁波或光子的双向传播,必然发生在光子的非极性且对称的两侧。在最低能量原理作用下,感生电动势平面与源电场平面相互垂直。垂直的电场不发生相互作用,唯有如此,方可满足能量最低原理。
这样,我们可以给出源处电磁波的空间形态如下
途中,源电场E伴随感生磁场B,感生磁场在x轴两侧各产生一个感生电动势,感生电动势与源电场垂直。
可见,源处电场变化产生的能量变量分成两份,沿与源电场垂直的左右侧发出两个光子(或电磁波)。
2.源的运动对光子的影响
通过上面的描述我们已经知道,经历半个周期的能量转换和转移,一个在源电场处与电场相关的能量的变量的一半被转移至源电场感生磁场空间扩布的边缘,这个量与源电场的变量的一半(离开源电场后为全部)相等,方向相反。
后面的电磁波将以这个新的源为中心,重复前半个周期的变化,差别仅仅在于方向相反。
可见,半个周期末时刻的源,已经足够引发新的电磁波或光子,因此我们说,完整周期(2π)对应的往复运动实际上可以产生两个方向相反的光子(或电磁波),而单向运动(比如电子的核子的跃迁),亦足够产生可传播的光子。
或者可以说,单向运动的电场变量产生一个光子,而振动(往复运动)产生两个光子。
同时由于磁场对电场变化的依赖性,往复振动产生的光子必然位于往复振动的两极,相差为π,相隔距离为振动幅度,且相互平行。
而对于无振动的源电场变化产生的两个电磁波,则在同一直线上传播,仅相差为π。
因为上述电磁波和光子模型的极性,我们用椭圆形(顶端为感生电动势)简图代表光子,则光子或电磁波与源的关系可如下图所示
上图的简要说明就是,在前π周期,时变电磁场随粒子向上运动,在π周期末感生一个反向的电动势,以这个电动势为源,生成新的电磁波;而粒子在源处达到顶点,往回反向振动,在2π周期末,在最初起点平面产生一个与最初的源电动势同向的电动势。
但是此时,以π周期末的反向电动势为源的新的电磁波在源上顶点平面继续运动,并在2π周期末形成一个与源电动势同向的电动势,这个电动势与紫色电动势一样,但空间位置相差半个周期的磁场扩布距离。
也就是说,当粒子运动到紫色圆点时,发生两个事件,其一是一个新的反向的电动势继续沿传播反向生成新的电磁波;其二是随粒子后半周期的反向运动,最终在源水平生成一个同向的电磁波。
当振动的不是粒子,而是原位的电场时,半个周期的电动势均生成电磁波,但同在一条沿传播方向的直线上,但是相差为π,距离相差半个波长。
五 光子或电磁波的波粒二相性
我们前述对光子或电磁波的描述,均建立在电磁波是一种波的基础之上,而且对电磁波能量转换形式、能量转移及位移机制,均以麦克斯韦电磁动力学为核心的电磁动力学为唯一的依据。
电磁波的波动特征显然是毋庸置疑的,但是,电磁波的空间特征和普通的物质波确实又大相径庭。
电磁波的波动特性表现为以下几点:
- 时变电场和时变磁场强度随时间呈周期性变化,这种变化与普通物质波相似,这是电磁波中时变电场和时变磁场强度的波动性;
- 电磁波在传播路径上半径逐渐扩大,到半个周期末达到最大值然后消失,遗留一个新的,与源电动势相距半个波长的电动势;然后一个新的电磁波从零开始重复前半个周期的变化,但是方向相反;
- 这样完整看一个周期,电磁波在空间上呈现为同传播距离和同振幅的波,如下图
可见,完整看一个周期的电磁波,就像两个在中轴线上连续的锥型结构,在空间呈现特殊的周期性变化。
同样,若将半个周期的电磁波当成一个时间上连续变化的整体,电磁波就是表现为锥形结构的粒子,而在某一个时刻,电磁波或光子则呈现为三联体结构的椭圆
整体看起来,也是一个粒子,只不过在周期的不同时刻,椭圆的长泾和短径分别取不同的数值,因而整体大小不同。
通过以上漫长的描述,我们基本上可以给出光子基本特征的总结了
- 光子本质上是时变的电磁场;
- 光子中的时变电场和时变磁场,作为电磁相互感应的基本特性,时变电磁场相互感生;
- 光子的本质是一种源电场变化产生的能量变量,以时变电磁场相互感生的方式在空间中进行能量转移,场的变化是光子中能量转移的方式,而不是能量本身;
- 感生磁场的空间恒速扩布,是光子位移和能量转移的基础;联合磁感生垫且位于磁场的磁力线上,两者联合实现光子的位移和能量转移;
- 光子在时变电磁场的强度变化上呈波动特征,空间上呈锥形的周期性涨缩;
- 光子在半个周期内呈现为锥形的粒子,某个时刻则表现为电场-磁场-电场三联体结构,以椭圆的空间特征呈现为粒子;
- 源处光子双向传播,离开源的光子沿直线单向传播;
- 前一个光子消失瞬间遗留一个电动势,新的光子以电动势为新的源再次生成,如此周而复始,驱使光子在空间中传播;
- 光子在传播路径上遵循能量守恒,电动势的变化不直接呈现;时变的电磁场中暗含一个相差1/2π的势,传播路径的任何时刻,势能和场能绝对值之和为恒定值,大小等于一个最小的能量单元。
- 光子在变化的强度和空间幅度上呈现周期性变化,具有波的特性;
- 光子具体时刻表现为电场-磁场-电场三联体结构,具有粒子特征。











