
你是否聽說過引起數學領域危機的 施瓦次燈籠(Schwarz lantern) ?施瓦次燈籠是一種特殊的幾何構造,它透過以特定方式排列的三角形來形成一個三維形狀。這個概念挑戰了我們對於幾何形狀表面積的直觀理解,展示了一些看似簡單的幾何問題實際上可能隱藏著復雜和出人意料的答案。今天,我們就來解構一下這個燈籠,看看它有何神奇之處。
讓我們以一個數學上的趣味問題作為開始,那就是「 圓周率等於4 」的悖論。這個悖論看似簡單,卻帶來了有趣的思考挑戰。首先,畫了一個直徑為1的圓。
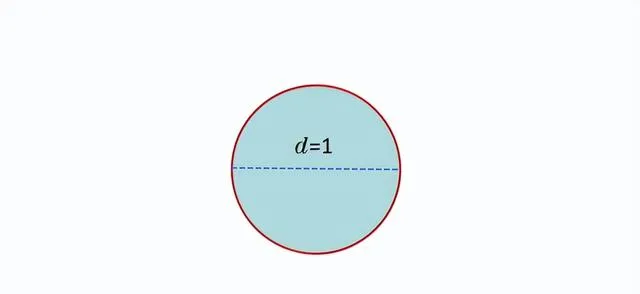
根據數學公式,這個圓的周長應該是圓周率π乘以它的直徑,也就是π。接著,我們在這個圓周圍畫一個邊長等於圓直徑的正方形。
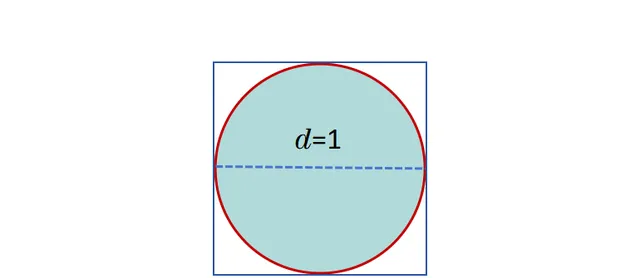
由於正方形四邊各為1,所以它的總周長就是4。現在,像下面這樣去掉四個角,
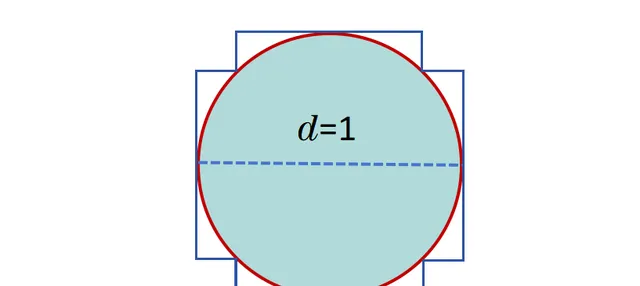
新形狀的周長仍然是4。同樣地,把新形狀的所有角切掉,周長仍然保持不變。

一直這樣操作,周長始終是4。與此同時,曲線的形狀越來越接近圓。我們得出結論,圓的周長等於4。換句話說,圓周率等於4。非常奇怪也很精彩。這個數學悖論已經存在了數百年,成為數學歷史上的一個經典案例,展示了幾何直覺和數學實際之間的差異。
阿基米德采用了一種與此類似的方法來估算圓周率的值。從包圍圓的正方形出發,他采取了這樣的方式:
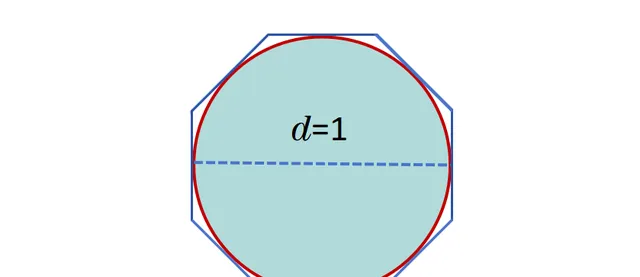
從而將正方形轉換成正八邊形。由於這種切角操作,得到的八邊形周長會小於4,略超過3.31。進一步切割八邊形的角形成正16邊形,其周長約為3.18多一點。透過繼續這樣切割角,得到的曲線逐漸逼近圓的形狀。與此同時,這些經過切割的曲線的周長也逐步接近圓周率的真實值。 由此可見,透過不同的方法近似圓形,可以得到不同的結果。
我們怎麽能確定哪一個是正確的呢?當涉及到像圓這樣的曲線時,它的長度究竟是多少?當然,對於直線,直接用直尺測量它的長度就可以了。但是對於一個平滑的曲線呢?怎麽測量它的長度?我們可以像這樣沿著曲線捲動尺子,
這說起來容易做起來難,但至少在理論上,這是定義和測量像這樣平滑曲線的長度的完全可行的方法。那實際操作呢?你會怎樣去估算這個曲線的長度?就像我們剛才做的那樣似乎是個好辦法: 用由直線段組成的另一個曲線來近似原曲線,並且逐段測量其總長度,來近似原曲線的長度。
那你會怎樣找到曲線的一個好的直線近似呢?首先想到是在曲線上挑幾個點,用直線連線它們。然後像這樣測量。

為了更精確地估計一條曲線的長度,我們可以采用逐漸細化的直線段來近似這條曲線。隨著這些直線段長度的減小,最終趨近於零,折線的總長度將更加接近曲線的真實長度。在處理平滑曲線時,數學上可以證明,只要這些分段的長度足夠小,接近於零,這種直線段近似的方法就能準確地給出曲線的實際長度。這種方法避免了之前在切割角落時出現的歧義性,因為它是基於將曲線劃分為越來越小的部份,直至它們的長度幾乎消失,從而達到精確測量曲線長度的目的。
當然,大多數人都知道,除了切角,阿基米德還像這樣精確地逼近圓來估計圓周率,

他透過構造緊密貼合圓形的內接和外切多邊形,從圓的內部和外部進行兩種不同的幾何近似。隨著這些多邊形邊數的增加,它們越來越逼近圓的實際形狀,從而使得對圓周率的估計更為精確。在這種方法的基礎上,阿基米德提出了他對圓周率的估計,

下面,我們看下施瓦茨燈籠的魔法。對於一個平滑的曲線,它的長度就是越來越精細的直線近似長度的極限。 顯然,類似的事情也應該適用於平滑的曲面,對吧?
拿球體為例,標記球體上的幾個點。將這些點連線成三角形。
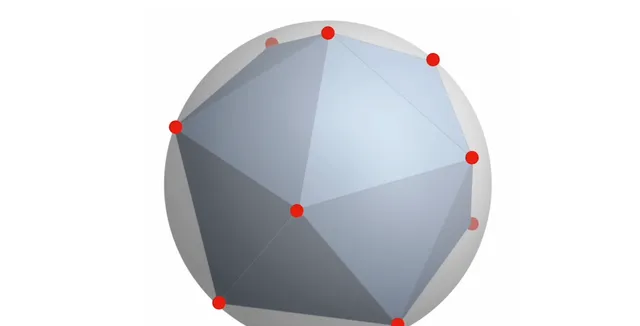
在球體上使用更多的點來獲得更好的近似。

這是對球體相當不錯的近似了,而且這個三角形近似的表面積很容易測量,肯定非常接近球體的表面積。
繼續精化,讓所有這些三角形邊縮小到零,這樣:
- 三角形近似應該與球體變得無法區分,
- 三角形近似的面積應該收斂到球體的表面積。
同樣的情況也應該適用於任何合理的表面。對吧?是也不是,真實的情況是,只要邊縮小到0,三角形近似就變得與表面無法區分。然而,它們的面積不一定接近球的表面積。
大約在1880年,數學家 赫爾曼·施瓦次( Hermann Schwarz ) 發表了他的著名的反例。

在他的反例中,一個圓柱面被一些三角形近似(像燈籠一樣)。
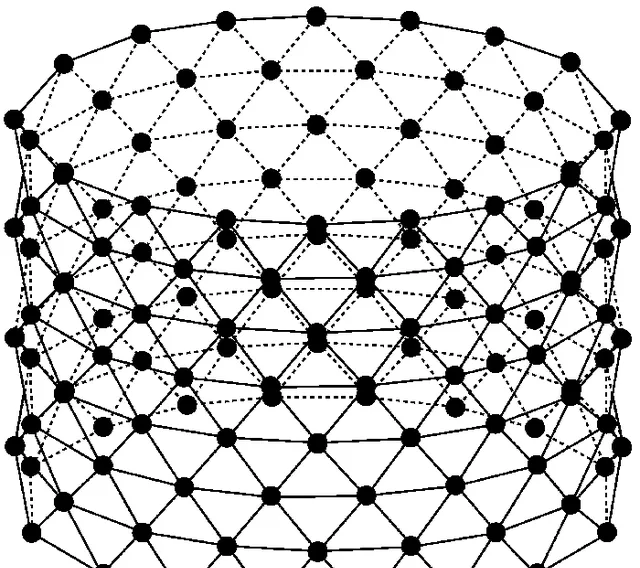
令人驚訝的是,如果你正確選擇這些特殊的三角形近似,隨著不斷細化,它們的面積並不接近圓柱的真實表面積。 實際上,你可以讓這個燈籠的面積接近任何大於或等於圓柱表面積的值,甚至可以讓它們接近無窮大。
這很瘋狂!這是一個大問題。如果我們采用直接計算表面積的常規方法,也就是透過逐步細化三角形來近似表面,即使是對於像圓柱這樣的簡單形狀,這種方法也可能會失敗。那我們怎樣才能可靠地計算表面積呢?解決這個難題成為了數學家的一項重大任務。
接下來,我會向你解釋施瓦次燈籠如何使我們的表面積計算方法失效,以及我們如何改進這些方法以準確計算表面積。此外,我還會講解圓周率等於4的悖論是如何被解決的。
所以,施瓦次燈籠是如何幹擾我們估算圓柱表面積的傳統方法的?
為了保持圓周率等於4的謎題,讓我們近似一個非常特殊的圓柱,一個表面積等於圓周率的圓柱。
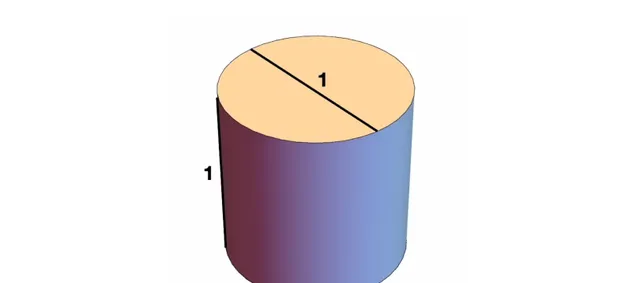
圓的直徑和圓柱的高都是1。圓的周長是直徑乘以圓周率,所以是圓周率。然後是藍色圓柱的面積,就是這個周長乘以高度,也是圓周率。
為了構造這個圓柱的燈籠近似,將圓柱分成四個相等的圓柱。在每個圓上放置七個等距的紅點,就像這樣,

再放入三角形,燈籠就形成了。

這個特定的燈籠有四個水平的三角形帶,並且每個級別上都有7個等距的紅點,可以表示為

為了得到越來越精細的圓柱燈籠近似,只需增加帶數和點數。
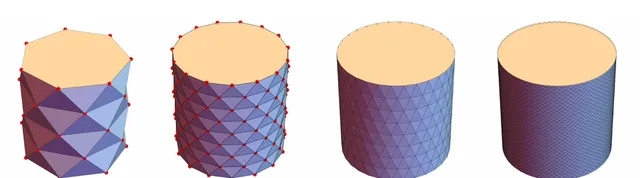
燈籠看起來越來越像圓柱,它們的面積接近圓周率。
現在做不同的操作:讓我們增加帶數,但點數p不變。

點數始終保持為5。燈籠的面積開始時是2.95,小於圓周率。但面積隨著帶數的增加而增加,
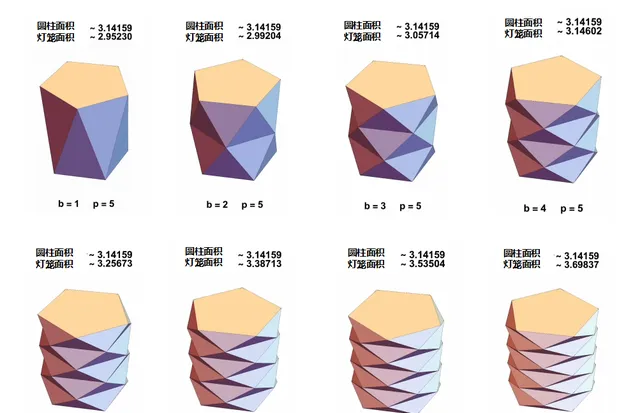
事實上, 這些燈籠的表面積會無限增大 !為了不用任何公式就能看出這是為什麽,只需看看,當我們逐漸增加構成燈籠的水平帶數時,可以觀察到每增加一層,燈籠的表面積都會以基本相同的量增加 。
隨著帶變得越來越薄,三角形將變得越來越平,每個帶基本上都添加了下面的灰色區域,

這個相同的面積被無限次地添加,導致面積無限大,燈籠的面積就會爆炸性地增長到無窮大!很容易看出,出於同樣的原因,將點數固定為任何其他數量,然後增加帶數,將導致面積無限大。
我們剛才看到的燈籠細化, 是施瓦次的著名反例嗎? 顯然不是 , 因為隨著燈籠的不斷細化,燈籠的面積朝著無窮大而不是圓周率發展。然而,這些特定的燈籠細化並不完全是我們想要的。為什麽?還記得我們為球體做的三角形細化嗎?所有三角形的邊緣都縮小到零。當邊緣縮小到零時,三角形近似變得與球體無法區分。
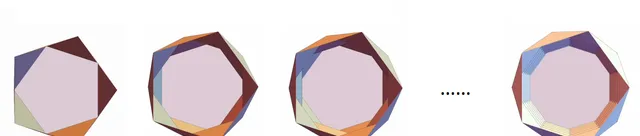
另一方面, 燈籠三角形細化中的邊緣並沒有縮小到零 。與此同時,燈籠最終並沒有變成圓柱。從頂部看,燈籠並沒有越來越像圓柱的頂檢視中的圓。從頂部看,燈籠越來越像這樣,

這是因為,到目前為止的燈籠細化中,我們只是增加了帶數而不是點數 。為了讓三角形邊緣縮小到零,並以這種方式保證燈籠近似與圓柱無法區分,我們必須讓帶數和點數同時無限增加。同時,我們想確保表面積爆炸性地增長到無窮大。聽起來很難,但這裏有一個重要的點要記住:讓這兩個數碼同時無限增加有許多不同的方式 。讓我們發明一種既滿足所有條件又能使邊緣縮小的方式。這就我們追求的反例。
我們從點數為4開始。對於b,選擇帶數的最小值,使得燈籠的面積大於4。
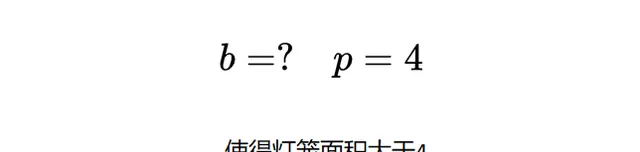
為什麽我們知道有這樣一個特殊的帶數呢?因為如果將點數固定在4,並增加帶數,面積就會爆炸性地增長到無窮大,所以在某個時刻,這個面積必須大於4。這個特殊的b恰好是7。所以,帶數為7,點數為4的燈籠是第一個燈籠。
下一個燈籠有5個點。這次的b是多少呢? 我們選擇b為使燈籠面積大於5的最小帶數 。這個特殊數碼恰好是15。
以此類推。下一個p是6,我們也希望它的面積大於6,滿足這一點的特殊帶數是26。
然後是p=7等等。現在,這種特殊的三角形細化滿足了我們所有的條件。點數和帶數都無限增加。這意味著三角形的邊緣會縮小到零 。因為邊緣縮小到零,燈籠的近似確實變得與圓柱無法區分 。最後,表面積爆炸性增長,因為我們確保了每個燈籠的表面積都大於點數p。第一個燈籠的面積大於4,下一個大於5,再下一個大於6,然後是7,8,9,依此類推。
還有其他燈籠三角形細化表現良好並給出了正確的面積。這裏有一個模式:4個點4個帶,5個點5個帶,6個點6個帶,等等。 當你做數學計算時,你會發現,這種燈籠細化的面積實際上確實收斂到圓周率,即圓柱的面積。
與我們的反例不同,燈籠表面的扭曲完全消失了,這意味著基本上每個小三角形都完全貢獻於構成圓柱的面積。透過更詳細地分析燈籠的面積公式,我們可以設計出燈籠細化,其面積接近於圓周率和無窮大之間的任何數碼。
例如,我們可以使極限面積為4。為了使施瓦次燈籠的構造與「圓周率等於4」的二維版本相似,我們可以選擇用一個表面積等於圓周率的球體來代替原來的圓柱。就像對圓柱一樣,對於球體乃至任何曲面,都可以套用施瓦次燈籠的病理性扭曲三角形細化方法。
現在,這種細化對於一些三角形有效,有些則不行。搞清楚哪些有效哪些無效不僅在理論上重要,而且在我們使用視覺化軟件表示三角化曲面時也很重要。如果軟件盲目地細化三角化,很可能會出現扭曲,這意味著因為三角形最終指向四面八方,虛擬光線不能以正確的方式反射,導致奇怪的視覺效果。
因此,在構建細化時,除了確保三角形的所有角都在目標表面上,並且三角形邊緣縮小到零之外,還必須確保三角形越來越好地貼合目標表面。 通常,透過關註其一個表面法線來衡量三角形貼合目標表面的程度,即與三角形成直角的尖刺,就像這個刺猬燈籠一樣。
如果尖刺指向四面八方,那麽就有很多扭曲。當你構建細化時,你想要追求的是, 近似中的尖刺盡可能垂直於目標表面 ,就像這樣,
以我們開始時的圓周率等於4的悖論細化為例。因為尖刺最終沒有與圓圈對齊,所以曲線的扭曲導致極限中的額外面積。
另一方面,如果所有角都在平滑的曲線上,並且邊緣縮小到0的直線近似中,尖刺會自動以正確的方式對齊。
你可能記得,文章開頭我提到了一個關於數學領域存在的困境。確實,盡管我們針對平滑曲線和曲面的測量問題似乎找到了簡單的解決方案,但這只是表面上的簡易性。我要強調的是,文章中討論的所有近似方法,主要適用於 光滑的幾何形狀 。然而,當面對那些極其扭曲或結構復雜的形狀,比如碎形曲線和曲面時 ,這些簡單的解決方法就不再有效,問題變得更加棘手。這種情況下,我們需要依賴於一種稱為 測度理論 的高級數學分支,這是一個專門研究如何準確測量復雜幾何結構的長度和面積的領域。











