幾何學與物理學相關並不奇怪——畢竟,空間是物理學發生的舞台。然而,實際上空間的幾何結構
對物理學的重要程度,以及我們宇宙的幾何結構
的奇特程度,遠超過我們想像。
如果要說物理學與幾何學之間迷人的相互作用
,有一位數學家有著第一手的經驗,他就是丘成桐。

曲率與重力
早在1915年,當艾拔·愛因斯坦(Albert Einstein)提出他的廣義相對論時,就初步暗示了空間不僅僅是一個物理背景
。愛因斯坦構建了一個四維時空
,這個時空由我們熟悉的三個空間維度
和一個時間維度
構成。他的理論革命性地提出,重力
不是一種在時空中穿行的無形的力,而是由大質素物體造成的時空彎曲
。想象一個放在彈床上的保齡球,它會形成一個凹陷,附近的物體(如彈珠)會滾入這個凹陷。同樣,廣義相對論認為,恒星和行星等大質素物體會像保齡球一樣彎曲時空,吸引著經過的物體。
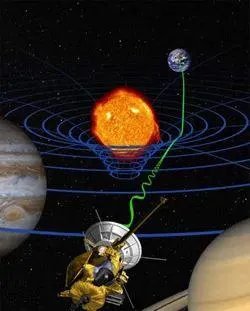
愛因斯坦的這種將空間、時間、物質和重力統一起來的觀點全新的——物理學家楊振寧將其描述為一種「純粹的創造」。然而,愛因斯坦用來描述時空曲率的數學並不是新創造的
。這一思想可以追溯到19世紀,當時數學家卡爾·佛烈德利赫·高斯
(Carl Friedrich Gauss)以及他傑出的學生伯恩哈德·黎曼
(Bernhard Riemann)提出了從內部測量物體曲率
的方法:他們不需要再參照物體所在的更大空間。這種內在的曲率概念正是愛因斯坦所需要的。
「在黎曼時代,沒有人相信他的新幾何學會有用
,」丘成桐解釋道。「但事實證明,它恰好符合愛因斯坦的目的
。沒有黎曼的工作,愛因斯坦可能需要更長的時間來發展廣義相對論。這成為了人們研究幾何學的重要原因:幾何學和物理學是互相推動,共同發展的。」
真空中的重力?
當丘成桐第一次了解廣義相對論時,他意識到廣義相對論提出了一個有趣的理論問題:是否存在一個不包含任何物質的時空——一個真空——但其中仍然存在重力?
我們生活的時空並不是廣義相對論唯一適用的時空。愛因斯坦場方程式,即描述廣義相對論的方程式,也允許其他解,例如一個既沒有物質也沒有重力的時空,在這樣的時空中,什麽都不會發生。但問題是,一個仍然具有曲率和重力的真空時空
是否存在?「在這樣的時空中,重力將因為拓撲(即空間的形狀)而不是物質而存在
。」丘成桐解釋說。
丘成桐後來意識到,數學家尤金尼奧·卡拉比
(Eugenio Calabi)在20世紀50年代就已經從幾何學的角度提出了這個問題。卡拉比對物體幾何形狀的精確特征,如大小和角度,與其拓撲結構之間的相互作用感興趣。拓撲對精細結構不敏感,只關註物體的整體輪廓
。例如,一個球和一個泄了氣的足球在幾何上有很大不同,但它們在拓撲上是相同的,因為這兩者不需要任何撕裂或切割就可以從一個物體變換成另一個物體。類似地,拓撲學認為甜甜圈和咖啡杯是等價的,因為一個可以連續變形為另一個。甜甜圈和球體的區別在於甜甜圈有一個洞。
具有給定拓撲的物體可以變形為許多不同的幾何形狀:球體變成泄氣的足球、金字塔或立方體等。卡拉比想,具有某種拓撲的形狀是否允許某種特定的幾何結構。如果答案是「是」,那麽在廣義相對論的框架下,所產生的物體可以被視為存在重力的真空。
卡拉比的問題
你可以想象出無數種拓撲形狀,但拓撲學家通常將他們的註意力限制在所謂的流形
上。這些物件在近距離觀察
時,看起來像我們熟悉的普通「平坦
」空間,即歐幾裏得空間。例如,球體和甜甜圈在局部看起來就像平坦的二維平面。如果你足夠小,就不會註意到它們的曲率,或者它們是否有洞。你可以很容易地在平坦的紙片上繪制球體或甜甜圈的一小塊。因此,這兩個都是二維流形
,也稱為曲面
。
球體和甜甜圈的另一個共同點是它們都是緊致的
:你只需要有限數量的二維對映即可覆蓋它們。這意味著它們的範
圍是有限的
。給定一個甜甜圈或球體,你總能找到一個足夠大的盒子來容納它,盡管這可能是一個非常大的盒子。
但是,流形不一定必須是二維的。還有三維流形
,從近距離看,它們就像是由三個垂直座標軸組成的三維歐幾裏得空間。由於從數學上講,你可以考慮任意維數的歐幾裏得空間(只需使用更多的座標,而不僅僅是三個),因此也存在任意維數的流形。
卡拉比對緊致流形的幾何特性特別感興趣,特別是曲率。想象一下,如果你給一個拓撲流形(比如一個球體)賦予一個特定的幾何結構(比如一個癟了的足球),你就可以測量流形上每個點的曲率。這並不總是直觀
的:想象一只螞蟻在馬鞍面上爬行,當它沿著馬鞍的頂部向上爬時,它會感受到向上的彎曲,而當它沿著馬鞍的兩側向下爬時,它會感受到向下的彎曲。在二維流形(比如我們想象中的馬鞍面)中,你可以將曲率與透過給定點的各種一維路徑相關聯
。
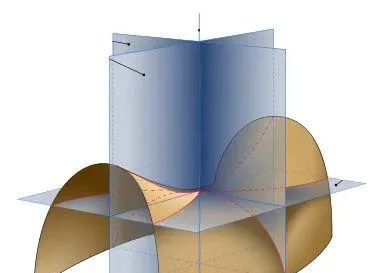
同樣,在更高維度中,你可以將曲率的概念與那些嵌入更大流形並包含你目標點的二維曲面聯系起來
。透過取這些二維曲面相關的所有曲率的平均值
,可以得到所謂的裏奇曲率
,即你所觀察的點的曲率。由於這是一個平均值,裏奇曲率只反應黎曼定義的完整曲率概念的一個方面。這意味著一個流形在每個點上都可以有零裏奇曲率,而不必整體上是平坦的(或者具有零黎曼曲率)。從物理學的角度來看,裏奇曲率捕捉到的部份恰好是描述由物質存在引起的時空彎曲的部份
。因此,具有零裏奇曲率的空間對應於沒有物質的空間,即真空。
但卡拉比對裏奇曲率感興趣完全是出於幾何學的角度。數學家陳省身在20世紀40年代證明了這樣一個事實:一個在每個點上裏奇曲率都為零的流形只能具有某種特定的拓撲結構。在二維空間中,這相當於普通的甜甜圈拓撲。
而在更高維度中,由零裏奇曲率表示的拓撲結構則更加難以描述。數學家們指出,具有這種拓撲結構的流形具有一個特殊性質,即它們的第一陳類為零。
卡拉比將陳省身的問題反過來考慮
:如果有一個緊致流形,其第一陳類為零,那麽能否將其變形為一個在所有點上黎奇曲率都為零的幾何形狀?換句話說,卡拉比想要知道,某種特定的拓撲結構是否一定存在相應的幾何形狀
。然而,卡拉比並不是研究一般的流形,而是專註於所謂的凱勒流形
(Kähler manifolds)。這些流形處理起來更簡單,因為它們偏離歐幾裏得空間很小,它們也被稱為復流形,這意味著在繪制這些流形的對映時,角度會被保留
,流形也展現出一定的局部對稱性。這種對稱性使得凱勒流形能夠被強大的數學工具所處理,並且賦予了它們一種特殊的對稱性。
丘成桐的回答

當丘成桐在20世紀70年代初開始研究這個問題時,他主要是出於對幾何學的興趣,不過,正如他告訴我們的那樣,「我一直在想這個問題對物理學也會很有趣:構建一個封閉的宇宙
(緊致流形),它沒有物質
(因為黎奇曲率為零),但仍然有重力
(由於其拓撲結構導致的曲率)。但這樣的結構的存在對幾何學也意義重大:卡拉比的猜想為理解裏奇曲率提供了一個最清晰的途徑。」
起初,丘成桐像其他大多數專家一樣,認為卡拉比的問題的答案是「不」。由於拓撲是一個比幾何更寬泛的概念,因此僅憑拓撲就能保證如此特殊的幾何類別似乎有點不可思議。「多年來,我試圖證明卡拉比追求的那種流形不存在,」他說。「但無論我嘗試什麽,我都會遇到困難。所以我認為大自然不可能這麽嚴重地玩弄我,我的推理肯定有問題。」
1977年,丘成桐最終證明了卡拉比是對的。為了完整地陳述他的結果,他證明了任何第一陳類為零的緊致凱勒流形都可以被賦予零裏奇曲率的幾何結構
。這些流形存在於所有維度中,後來被稱為卡拉比-丘流形
。
隱藏的維度
1982年,丘成桐因解決了卡拉比猜想而獲得費斯獎,這是數學界最高的榮譽,這一突破對幾何學以及其他領域產生了深遠的影響。直到後來他才知道,卡拉比-丘流形正是某些物理學家一直在尋找的東西。他回憶說:「有一天(1984年),我和妻子在聖地亞哥,眺望美麗的海洋。突然電話響了,是我的朋友安德魯·斯特羅明格(Andrew Strominger)和加利·霍洛維茨(Gary Horowitz)打來的。他們很興奮,因為弦論家
們正在構建宇宙的模型,需要知道卡拉比-丘流形
是否真的存在。我欣然告訴他們,這些流形確實存在。」
弦論試圖成為一種「萬物理論」,用以解釋宇宙中的所有物理現象。這樣的理論曾經是,現在仍然是物理學的聖杯,因為現有的兩個主要理論——廣義相對論(描述宏觀世界)和量子場論(描述亞原子尺度世界)——相互矛盾。弦論透過提出最小的物質和能量單位不是點狀粒子,而是一根根微小的弦
,從而解決了數學上的矛盾。這些弦可以振動,就像吉他弦可以振動一樣,不同的振動類別對應著我們觀察到的基本粒子和物理力。
在20世紀80年代初,弦論還處於起步階段。它面臨的一個主要問題是,為了理論的自洽性,它需要十個維度
。粒子和力被認為來自於弦振動的所有不同方式。如果維度少於十個,那麽就不足以產生所有觀察到的物理現象。另一方面,如果維度超過十個,弦論可能會產生一些荒謬的結果。因此,精確的十個維度是必要的。但問題是我們為什麽只能感知到其中的四個維度,即三個空間維度和一個時間維度?

弦論對這一謎題的回答是,六個額外的維度被緊緊地卷曲在一個極其微小的空間中
,這個空間小到我們無法直接感知。丘成桐解釋說:「在我們所觀察到的四維時空中的每一個點,實際上都存在著一個微小的六維空間
。」這些微小的世界太小了,以至於我們無法察覺它們的存在。那麽,什麽樣的六維幾何結構
能夠容納這樣一個隱藏的世界,並滿足弦論的其他要求呢?答案已經很明顯了:它必須是一個六維的卡拉比-丘流形
。丘成桐補充道:「卡拉比-丘流形最終為弦理論提供了一個具體的幾何模型。」
卡拉比-丘流形對弦論具有吸重力的一個原因是它們的緊致性:這些流形非常小,直徑大約在10厘米左右,比一個電子小上萬億倍。但是還有其他原因。為了與當時的物理理解保持一致,隱藏維度的流形必須具有零裏奇曲率
。更重要的是,弦論假設了一種特殊的對稱性,稱為超對稱性,這對時空幾何提出了特殊要求。這些要求使得卡拉比-丘流形(具有特殊的凱勒對稱性)成為弦論的絕佳候選者,盡管我們仍然不知道它們是否是維度難題的唯一可能解決方案。
弦論未來
伴隨著卡拉比-丘流形的發現和其他重大進展,1984成了弦論發展史上具有裏程碑意義的一年。但故事並沒有就此結束。1986年,弦論遭受了一個小挫折,當時發現弦論需要卡拉比-丘流形的一個輕微修正版本,其裏奇曲率不是零,而是非常接近零
。更糟糕的是,有許多不同的六維卡拉比-丘流形可能符合弦論的要求,而且沒有人能夠計算出哪個是「正確」的。所有這些都某種程度上削弱了卡拉比-丘流形在物理學中的地位。然而,當人們發現成對的不同的卡拉比-丘流形可以產生具有相同物理學的理論宇宙時,另一個推動力出現了。這種流形對激發了新的興趣,並產生了一種新的對稱性概念,稱為映像對稱(這個名字有些誤導,因為它比名稱所暗示的要復雜得多)。
映像對稱的確切物理意義仍然是一個謎,但是,正如丘成桐所說,它導致了「對卡拉比-丘流形的驚人的新理解。並激發了許多豐富的數學成果,這些成果完全是由弦論的直覺所驅動的。」 特別是,新的映像對稱概念解決了一個幾何分支中幾乎被遺忘的長達一個世紀的問題。我們不準備在這裏討論這個問題,只說它涉及到計算特定幾何空間中的曲線的數量。映像對稱提供了獲得答案需要的公式,後來丘成桐和同事們證明了其正確性。
今天,弦論仍然遠未完善。有許多物理量它還無法描述。而且它還沒有,目前也不能在實驗室中進行測試。然而,丘成桐相信,弦論純粹的數學一致性意味著它不會是一個誤區。「數學家們已經能夠證明由弦理論的物理直覺所激發的公式。弦論對數學的許多其他驚人貢獻也是不可忽視的
。因為弦論的存在,許多表面上不同的數學領域已經以一種平滑但完全意想不到的方式融合在一起。這意味著弦論中一定有一些真實的成分。它最終會引匯出一個關於物質的基本理論嗎?現在說還為時過早,但我們相信它提供的直覺中一定有一些真理。」
作者:Marianne Freiberger
轉譯:K.Collider
審校:小聰
原文連結:Hidden dimensions
編輯:利有攸往
轉譯內容僅代表作者觀點
不代表中科院物理所立場











