第三章 一次函數
在第二章裏,我們曾經看到過象
W =7.8V, y =0.6x,
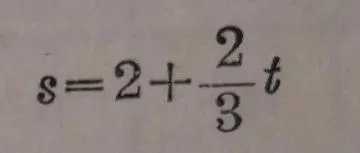
之類的函數.這些函數的共同特點是等號右邊的式子都是自變量的一次式。通常我們把具有這種特點的函數叫做關於這個自變量的 一次函數 。它是函數中最簡單的一類。這一章裏,我們將研究這類函數。
§3.1函數 y = kx ( k ≠0)
1.正比例關系 我們來考察§2.1裏舉過的鐵的重量 W 和它的體積V之間的函數關系:
W =7.8V,
這裏7.8是每立方厘米的鐵塊重量的克數.
如果令鐵的體積分別是1立方厘米,2立方厘米,3立方厘米,……就可以算出和它對應的重量如下表:
表格

這裏我們看到:當體積 V 擴大(或者縮小)若幹倍的時候,重量 W 也隨著擴大(或者縮小)相同的倍數.在算術裏,我們已經知道具有這樣性質的兩個量,叫做 成正比例關系的量 .
從這個表裏,我們還可以看到: W 的任何一個數值和它所對應的 V 的數值的比,是一個常數.例如
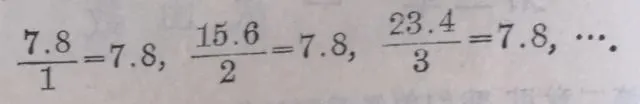
一般地,我們有

這裏常數7.8叫做變量 W 和 V 間的比例系數。
因為在算術裏,我們所學過的數只有正數和零,所以當時所研究的成正比例的量的比例系數都是正數.現在,我們已學習了負數,需要把算術裏學過的成正比例的量的定義加以推廣。
我們來看下面的例子:
一列火車,以每小時40公裏的速度,自東向西行駛,在中午到達甲站。求在中午以前½小時,1小時,3/2小時,以及中午以後½小時,1小時,3/2小時,火車離開甲站的距離.
我們把自西向東的方向作為正的方向(圖3·1),那末這列火車行駛的速度可以記作
v =-40公裏/小時。
圖3.1
設在中午後 t 小時(在中午以前, t 用負數表示;中午以後, t 用正數表示)火車離開甲站 s 公裏(在甲站以東, s 是正數;在甲站以西, s 是負數)。那末可得 s 和 t 之間的函數關系
s =-40t.
這樣就得到下面的表:
表格

這裏,我們也可以看到 s 的每一個值和它對應的 t 的值的比是一個常數,就是
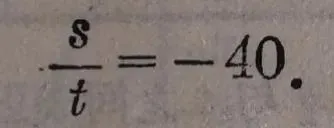
我們也把變量 s 和 t 之間的這種關系叫做正比例關系,把這個常數"-40"叫做 s 和 t 之間的比例系數.
一般地說:
兩個變量 y 和x間的函數關系,如果能用公式
y = kx(這裏 k 是一個不等於零的常量)
來表示,那末這兩個變量間的函數關系就叫做正比例關系, k 叫做比例系數。
習題3.1(1)
1.下列各種關系裏,哪些是正比例關系?為什麽?
(1)正方形的周長 p 和它的一邊的長 a ;
(2)正方形的面積A和它的一邊的長 a ;
(3)圓的周長 C 和它的直徑 d ;
(4)圓的面積 A 和它的直徑 d ;
(5)速度 v 一定的時候,所走的距離 s 和所需的時間 t ;
(6)時間 t 一定的時候,運動的速度 v 和所走的距離 s;
(7)距離 s 一定的時候,運動的速度 v 和所需的時間 t ;
(8)比重 d 一定的時候,物體的重量 W 和它的體積 V ;
(9)體積 V 一定的時候,物體的重量 W 和它的比重 d ;
(10)重量 W 一定的時候,物體的體積 V 和它的比重 d .
2.把上面這些關系中,成正比例關系的寫成 y = f ( x )的形式,並求出每一個關系中的比例系數.
3.把汽油用均勻的速度註入桶裏。註入的時間和註入的油量如下表:
表格
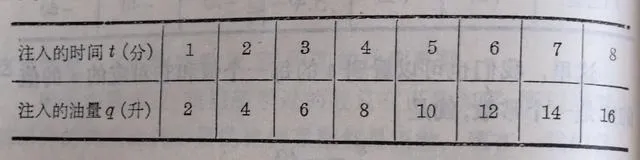
(1)從表裏的數據,證明 q 與 t 之間成正比例關系;
(2)求比例系數(q/t);
(3)用解析法表示出 q與 t (把 t 作為自變量)之間的函數關系;
(4)求 t =1.5, 4.5時 q 的對應值.
2.函數 y = kx 的影像 我們先來作下面這兩個函數的影像:
(1) y =2x, (2)y=-2x
用§2.7裏講過的方法,我們先選擇一些x的值,列成下表:
表格
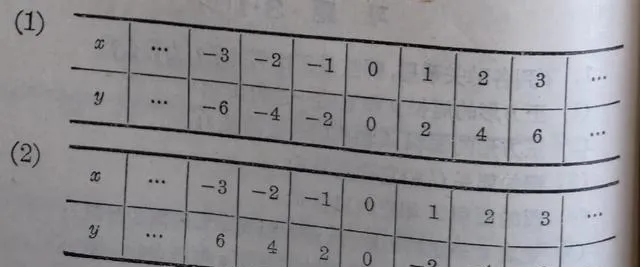
把表裏的每一組 x , y 的對應值作為點的座標,在直角座標系裏作出這些點,並且用平滑的線連線起來,就得到圖3.2和圖3.3.
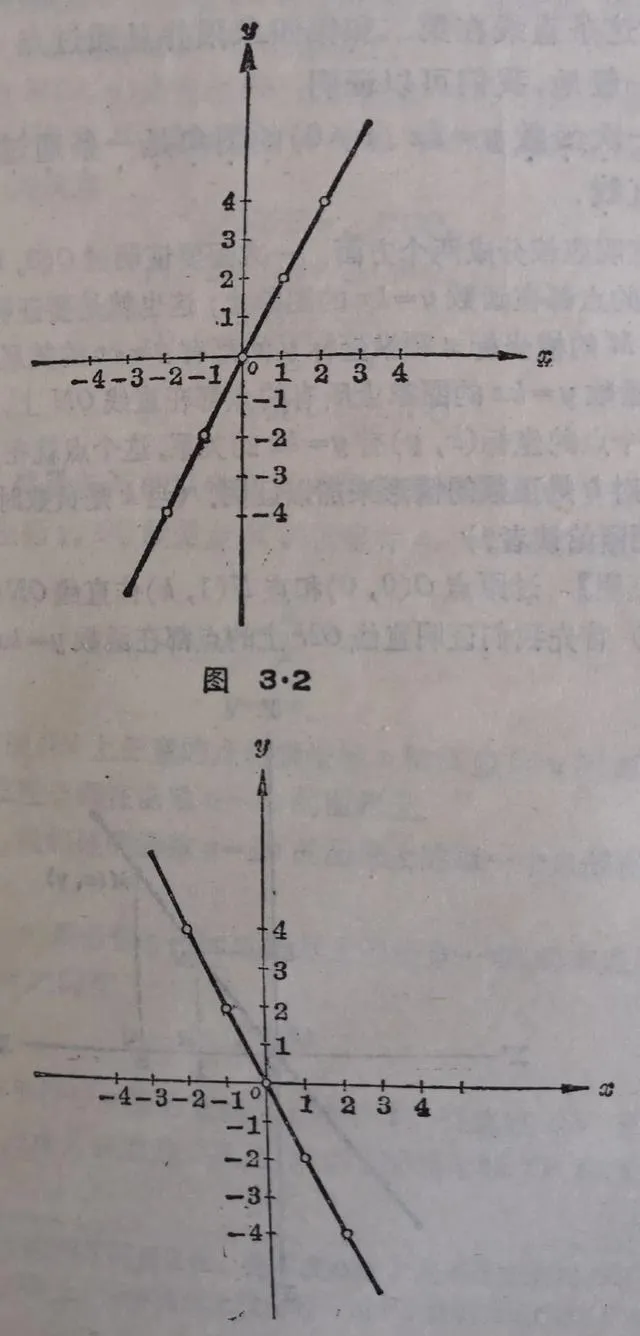
從圖裏可以看到這兩個函數的影像都是透過原點的直線.在(1)中這條直線在第一第三象限並且透過點(1,2) ;在(2)中這條直線在第二和第四象限並且透過點(1,-2).
一般地,我們可以證明:
一次函數y= kk (x≠0)的影像是一條透過原點和和點(1,k)的直線.
*證明應該分成兩個方面.一方面要證明過O(0,0)和 N (1,k)的直線上的點都在函數y= kx 的影像上;這也就是要證明,直線 ON上的每一點 M 的橫座標x和縱座標 y 間都有y= kx的關系。
另一方面還要證明,函數y=kx 的影像上所有的點都在直線 ON 上,這就是要證明,如果一個點的座標(x ,y)有y=kx的關系,這個點就在直線 ON 上.下面我們對k是正數的情形來加以證明.(當 k 是負數時,可以同樣地證明,證明留給讀者.)
【證明】過原點O(0,0)和點 N (1,k)作直線ON(圖3.4).
(1)首先我們證明直線ON上的點都在函數y= kx 的影像上.
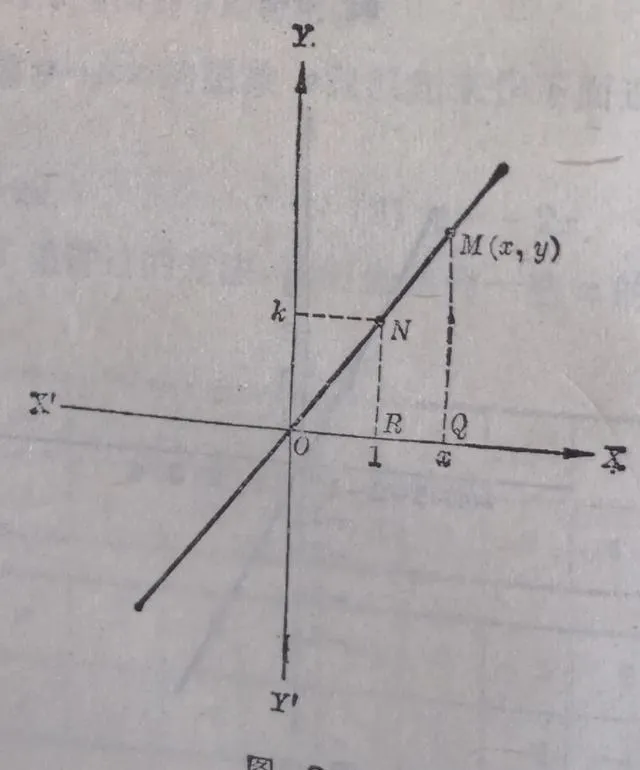
圖3.4
因為原點 O( 0 ,0)的橫座標 x 和縱座標 y 之間有
0= k·0
的關系。所以原點 O 在函數 y =kx 的影像上。同樣地,因為k=k·1,所以點 N (1, k )也在函數 y=kx的影像上。
現在設點 M ( x , y )是直線 ON 上的任意一點。過點 N 和 M 分別作 y 軸的平行線 NR 和 MQ 交 x 軸於 R 和 Q .因為在直角三角形 ONR 和 OMQ 中,有一對銳角
∠NOR =<∠MOQ ,
∴△ONR ∽△OMQ .
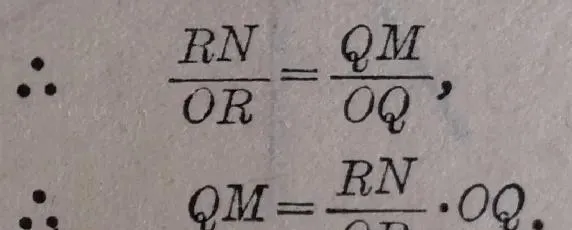
這裏 RN 就是點 N 的縱座標 k , OR 就是點 N 的橫座標1; QM 就是點 M 的縱座標 y , OQ 就是點 M 的橫座標 x 。代入上面這個等式,就得到
就是
y = kx .
這就證明了直線 ON 上任意的點的橫座標 x 和縱座標 y 間都有 y = kx 的關系,因此這些點都在函數 y = kx 的影像上。
(2)其次,我們證明函數y=kx 的影像上的每一個點都在直線 ON上.
設點 P ( x , y )是函數 y = kx 的影像上的任意一點,那末點 P 的縱座標 y 和橫座標x 之間有
y = kx
的關系.
過點 P 作平行於 y 軸的直線交 x 軸於 T ,交直線 ON 於 V ①(圖3.5)。那末因為點 V 在直線ON上,所以它的縱座標 TV和橫座標OT間有
①這裏我們套用了間接證法。先不考慮點 P 是不是在直線 ON 上,故意把它不畫在直線 ON 上,而在直線上找出另一點 V ,然後再證明點 P 和點 V ー定重合。
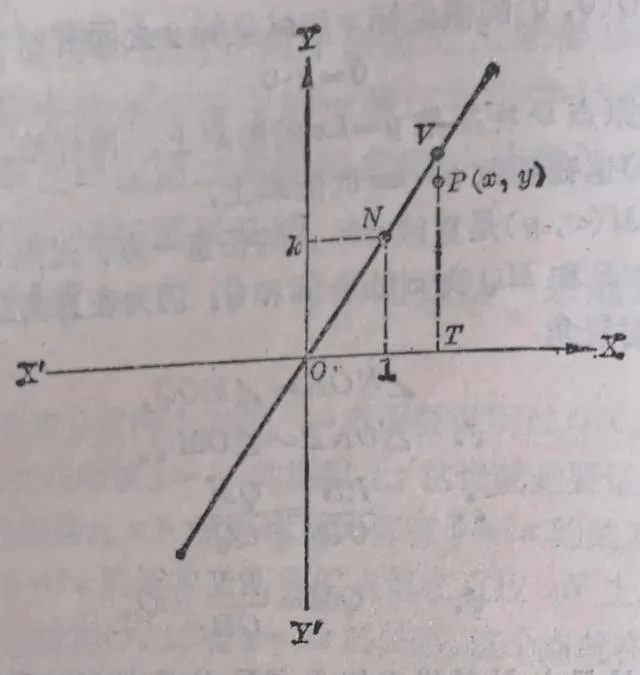
圖3.5
TV=k·OT
的關系.
但是,我們已經知道,點 P 的縱座標 y(就是TP)和橫座標x(就是OT)之間有
y = kx ,
就是
TP= k·OT
的關系。因此
TP=TV .
所以,點 P 一定和點 V 重合,也就是說,點 P 在直線 ON 上。這就證明了函數y=kx的影像上的任意一個點都在直線 ON 上。
函數y=kx的影像,以後簡稱為直線 y=kx .
例1.作函數 y=½x 的影像。
【解】列表:
表格

作圖:
圖3.6
註 要畫出一條直線,只要找到直線上的任意兩點就可以了。為了使畫出的圖精確些,我們所取的兩個點要使它離開得遠一些,所以這裏我們取(4,2)這個點,而不是取1,½)這個點.
習題3.1(2)
1.用描點法作出習題3.1(1)裏第3題函數 q = f ( t )的影像。
2.在同一座標系裏作函數
(1) y = ½x ; (2) y = x ;
(3) y =2x; (4) y =-½x
(5) y =- x ; (6) y =-2x
的影像。
3.一個物體以每小時3公裏的速度作勻速運動,
(1)把這個物體在 t 小時內所經過的路程s公裏用公式表示出來;
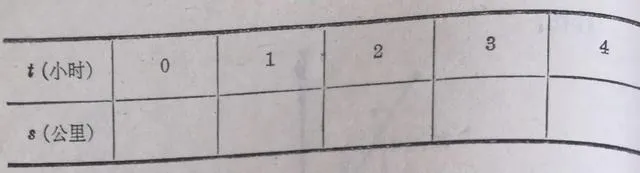
(2)填寫下面的表:
表格
(3)根據表裏的數值,畫出這個物體運動的路程和時間的關系的影像;
(4)根據影像找出 t =1½, t =3½時 s 的值;
(5)根據影像找出 s =27, s=10時 t 的值。
*4.證明,當 k <0的時候,函數 y=kx 的影像是經過原點,並且在第二和四象限的一條直線。
3.函數 y = kx 的性質
觀察圖3.2和圖3.3,容易發現函數 y = kx 有下面的重要性質:
(1)如果k >0,那末當自變量 x 逐漸增大時,函數 y 的值也隨著逐漸增大;這時我們說函數 y=kx 是 上升 的;
(2)如果 k<0,那末當自變量x逐漸增大時,函數的值則隨著逐漸減小,這時我們說函數y= kx是 下降 的.
4.直線 y = kx 的斜率和傾角
現在我們來研究當比例系數 k 變化的時候,直線 y = kx 的位置怎樣變化.
例2.在同一個直角座標系裏,作下面三個函數:
(1) y =½
(2) y = x ;
(3) y=2x
的影像.
【解】在習題3.1(2)裏,我們曾經作出這些函數的影像(圖3.7).
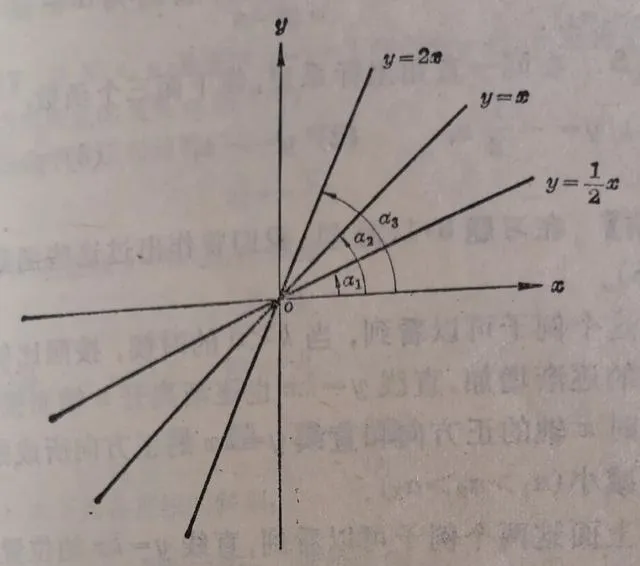
從這個例子可以看到,當 k >0的時候,按照比例系數的逐漸增加,直線就逐漸離開x軸而接近 y 軸.這時直線y=kx的正方向①和 x 軸的正方向所成的角α在逐漸增大(α₁<α₂<α₃).
例3.在同一直角座標系裏,作下面三個函數。
(1) y =-½x;
(2) y=-x ;
(3)y=-2x
的影像.
【解】在習題3.1(2)裏,我們曾作出過這些函數的影像(圖3.8).
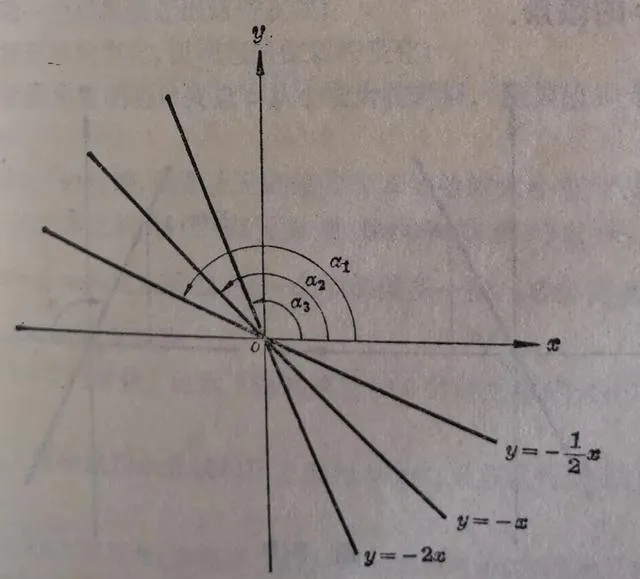
從這個例子可以看到,當k<0的時候,按照比例系數的絕對值的逐漸增加,直線y=kx也逐漸離開 x 軸而接近 y 軸。但是這時x軸的正方向和直線y=kx 的正方向所成的角α卻在逐漸減小(α₁>α₂>α₃) .
從上面這兩個例子可以看到,直線 y = kx的位置,和它的比例系數 k 有關。我們把 k 叫做直線 y = kx 的 斜率 ,並且把x軸的正方向和直線 y = kx的正方向所成的角α ,叫做直線 y =kx的 傾角 。
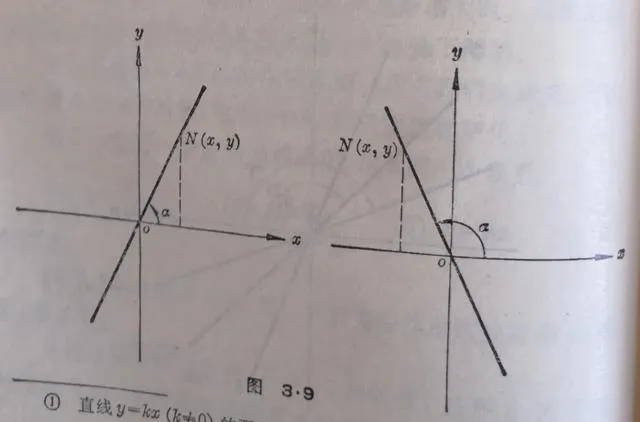
圖3.9
①直線 y=kx( k≠0)的正方向指的是向上的方向。
*利用三角學中的知識,我們可以證明
k = tan α .
【證明】設 N ( x , y )是直線 y = kx 上的任意一點, x軸的正方向和直線向上方向所成的角是α(圖3.9).
根據三角學中正切函數的定義,得到
tan α =y/x (1)
但是, N 在直線 y = kx 上,所以有
y/x=k. (2)
從(1)和(2)得
tan α = k .
習題3.1(3)
1.(1)求下列各直線的斜率
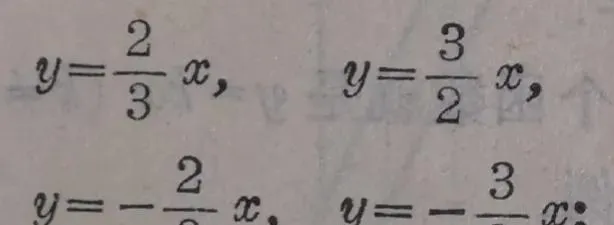
(2)在同一座標系裏作出這些直線;
(3)根據斜率的變化,說明直線位置的變化;
(4)根據影像說明當自變量 x 從小增大的時候,函數值的變化情況;
(5)當 k >0的時候,函數上升的速度和 k 的值的大小有什麽關系?
[提示:從影像上研究,當自變量增加同一數值的時候,函數
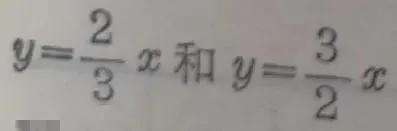
所對應的值,哪一個增加得多一些。增加得多的,就說這個函數上升的速度較快.]
(6)當k< 0 的時候,函數下降的速度和 k 的絕對值的大小有什麽關系?
*2.求上題中這四條直線的正方向與x軸的正方向所成的角(精確到1°)①
①如果沒有學過三角,本題可以暫時不做;如果只學過銳角的三角函數,那麽可以只做k>0的時候的兩個小題。
上期連結:https://m.toutiao.com/is/iNygsUFT/ - 名師徹底講透初等函數(7)函數影像的繪制 - 今日頭條
下期預告:§3.2 函數y=kx+b(k≠0)
科學尚未普及,媒體還需努力。感謝閱讀,再見。











