西風 發自 凹非寺
量子位 | 公眾號 QbitAI
Transformer中的資訊流動機制,被最新研究揭開了:
所有層都是必要的嗎?中間層在做同樣的事嗎?層的順序重要嗎?
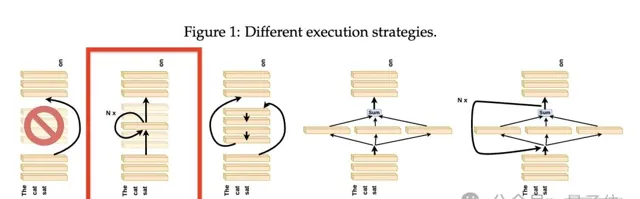
如果跳過一些層
,比如第4層輸出接到第6層會怎樣。隨機打亂層的順序
,比如4-6-5-7又會怎樣。
最近一項名為「Transformer Layers as Painters」的研究火了,由來自AI初創公司Sakana AI、Emergence AI的研究團隊完成。

他們從Transformer內部工作原理出發,經過一系列實驗對以上問題得出了結論。團隊表示深入理解這些原理不僅能提高現有模型利用效率,還能幫助改進架構開發新的變體。
谷歌DeepMind研究員、ViT作者Lucas Beyer看過後直接點了個贊:
很棒的總結!盡管一些實驗在之前的研究中已經被展示過了,但我喜歡你添加的新細節,特別是強調了「推理」類任務比其他任務受影響更大!

還有不少學者、工程師也表示強烈推薦。
敢打賭,其中一些見解最終將會用於改進Transformer。

其中的實驗再次證實了:復制層對創造性任務有幫助,但對推理任務通常無效;改變層的順序行不通;剪枝在中間層效果最佳,但仍需要進行修復調整。
所以,在這項研究中,研究團隊都進行了哪些實驗?回答了哪些問題?
實驗模型選擇和基準
先來看一下實驗配置~
實驗在decoder-only
和encoder-only
模型上進行。
其中decoder-only模型選擇的是Llama2
,主要研究32層、70億參數的Llama2-7B,擴充套件實驗中也包含13B(40層)和70B(80層)模型。
encoder-only模型選擇的是BERT
,有24層、3.4億參數。
研究人員使用這些模型的標準預訓練checkpoints。在所有實驗中,模型都是凍結的,除BERT的評估中包含一個標準的微調步驟,其它情況未透過微調等方法修改模型參數。
基準測試方面,Llama2使用以下標準基準:ARC(科學考試問題)、HellaSwag(常識問題)、GSM8K(數學題),WinoGrande(常識推理)、LAMBADA(詞匯預測)。其中LAMBADA用於測困惑度,與訓練期間使用的原始token預測最接近。
對於Llama2的效能評估,提供了基準測試的標準化中位數,將效能從0到1(模型最優效能)進行量化。
對於BERT,采用GLUE基準並遵循其評估指標,包括基準的未標準化平均分。註意,標準的BERT評估包括一個微調步驟,因此對模型進行了適應力調整。在附錄中研究人員也展示了一個只有模型頭部可以調整的評估結果。
實驗動機最初源於這樣一個問題:
是否可以將多個層以某種方式合並成一個可能更大的單一層?
假設可能由於訓練過程中使用了殘留誤差連線,神經網絡的中間層可能使用了一個共同的表征空間。
(對於標準的多層感知機來說不成立,它們之間沒有促使共同表征或層間排列一致性的機制)
如果層能共享一個表征空間,將對後續條件計算或向預訓練Transformer模型動態添加新知識及下遊套用產生重要影響。
關於Transformer的8大問題
層是否使用相同的表征空間?
為確定不同層是否共享相同的表征空間,研究人員檢驗了Transformer對於跳過特定層或更改相鄰層順序
的魯棒性。
例如,在Llama2-7B模型中將輸出流從「第4層->第5層->第6層」的正常順序,改為「第4層->第6層」,跳過第5層,會怎樣?
又或者將第4層的輸出送到第6層,然後將第6層的輸出送到第5層,再送到第7層,會怎樣?
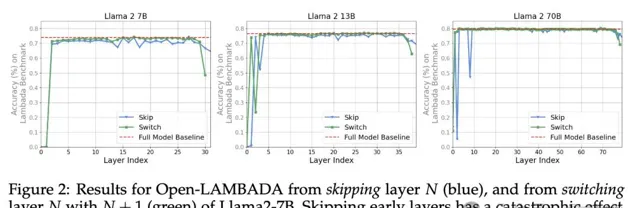
如下圖所示,實驗發現除了最前面的和最末尾的幾層,Llama2-7B跳過或改變層序表現出很好的魯棒性
。
也就是說,中間層共享一個表征空間,中間層與「外層」(最前面的和最末尾的幾層)具有獨立的表征空間。
為了進一步證實這一假設,研究人員測量了不同模型(Llama2-7B、Llama2-13B和BERT-Large)中不同層的隱藏狀態啟用之間的平均余弦相似度,並跨基準測試進行了比較。
下圖3展示了所有中間層之間的一致性
。例如,底部第四層的啟用與頂部第四層的啟用高度相似。對於40層的Llama2-13B,可以看到這些層按相似性可劃分成4-5個組:第0層,1-3層,中間層,然後是最後一兩層。
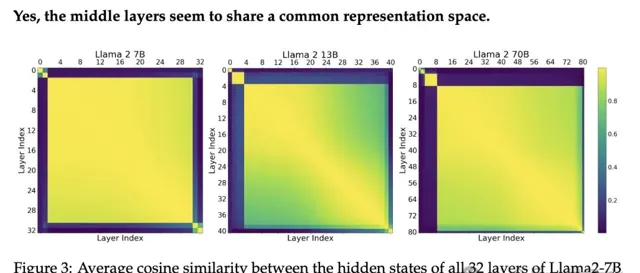
這表明模型可能對「開始」、「中間」和「結束」層具有三個不同的表征空間
。研究人員還發現,「開始層」的數量似乎隨著模型總層數的增加而增加。
此外,高余弦相似度可能證明有一個共享的表征空間,低相似度更能表明這些空間不是共享的。而上圖3中Llama2-7B的數據與圖2所示的效能結果高度一致,這進一步證明了:
至少中間層的表征空間是共享的。
所有層都是必要的嗎?
為了進一步驗證中間層的表征空間真正共享,研究人員還進行了層跳過實驗
(實驗中未進行任何微調)。
具體來說,將第N層的輸出直接傳遞為第N+M層的輸入(M>1),從而「跳過」了M-1層,如下圖所示。
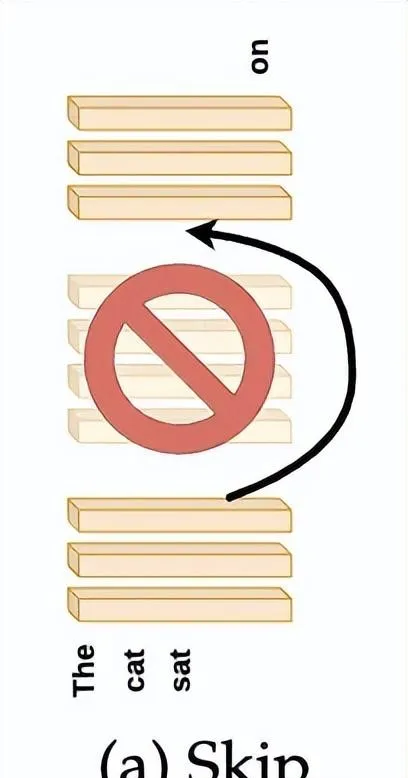
原本第N+M層僅針對來自第N+M-1層的輸入進行訓練,那麽現在它能否理解第N層的啟用?
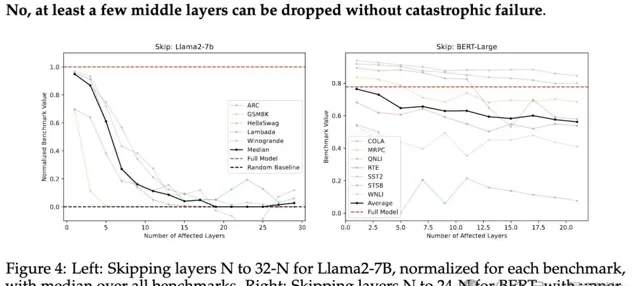
此類實驗中,研究人員正常執行第一層和最後N-1層,而跳過或修改第N+1到第T-N層(T是模型總層數)。
如下圖4,在多個基準測試中,Llama2-7B和BERT-Large的效能均逐漸下降
(圖從左至右展示了跳過層數逐漸遞增的變化)。這一結果揭示了:
不是所有層都是必要的,至少省略部份中間層不會對整體效能造成嚴重影響。
中間層是否都執行相同的功能?
如果中間層共享一個共同的表征空間,這些層是否多余?
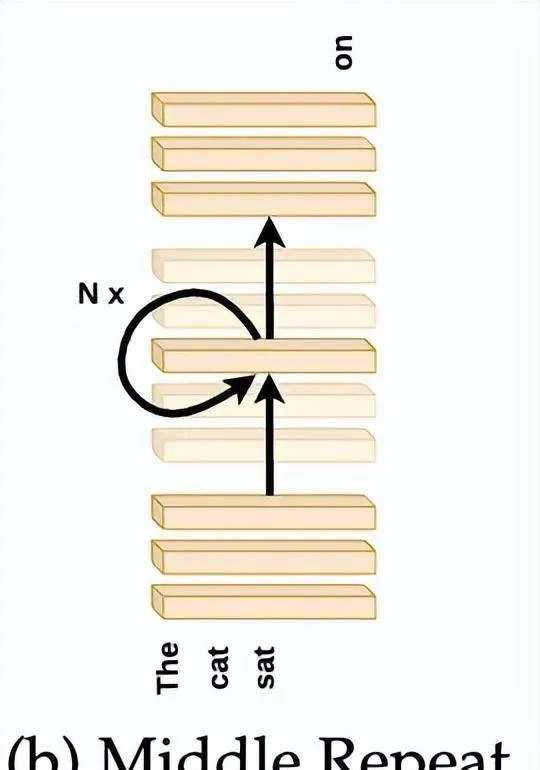
為了解答該問題,研究人員重新進行了前面的「跳過」實驗,但這次不是跳過中間層,而是用最中心層的權重替換了這些所有中間層的權重
,如下圖所示。
實際上就是在最中心層上迴圈執行了T-2N+1次,其中T是模型總層數(Llama2-7B為32層,BERT-Large為24層)。
結果基準測試中,隨著被替換的層數增加,模型效能迅速下降
。而且效能下降速度比僅僅跳過某些層要嚴重得多,這種權重替換極具破壞性。
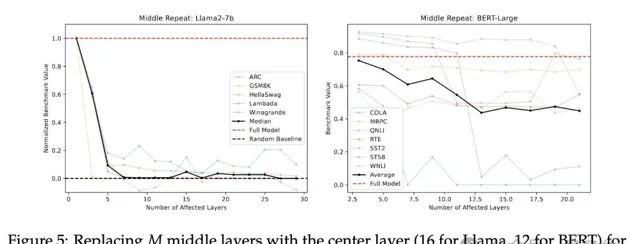
因此,中間層各執行不同的功能並非多余,中間層之間共享權重會產生災難性後果。
層的順序重要嗎?
上面實驗表明中間層雖共享表征空間,卻在該空間上執行不同操作。那麽這些操作順序重要嗎?研究人員進行了兩組實驗。
首先,將中間層按照與其訓練順序相反
的順序(逆序)執行。將第T-N層的輸出傳遞給第T-N-1層,依此類推,直至第N層,然後將該層的輸出傳至最後的T-N層。
如下圖:
第二個實驗,隨機排列
中間層順序,並平均10個隨機種子結果。
結果如下圖,兩種情況模型都呈現出緩慢的效能下降
。
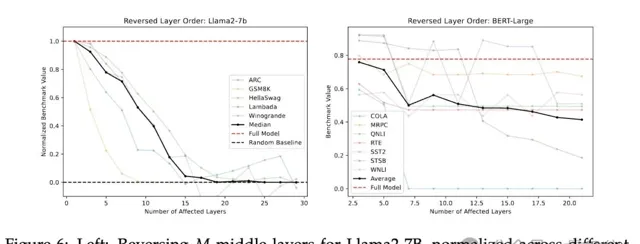
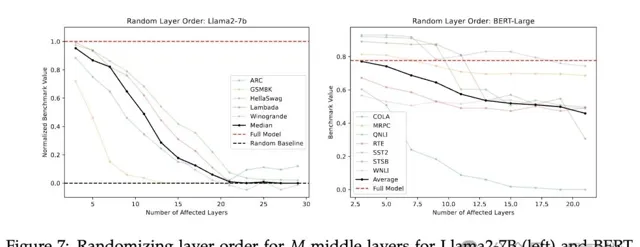
這裏劇透一下下面的一項實驗結果,無論是逆序還是隨機順序,模型表現均優於直接跳過這些層,說明即使層在非訓練順序的輸入上執行,依然能進行有效輸出。
因此,層順序重要嗎?結論是:
層順序調整對效能有一定影響,隨機順序和逆序都表現出一定的效能退化。
值得註意的是,隨機順序效能優於逆序。可能是因為逆序與訓練時的順序完全相反,而任何隨機順序都至少保持了一些順序上的連貫性(即某層i總在另一層j之後,其中i>j)。
可以並列執行這些層嗎?
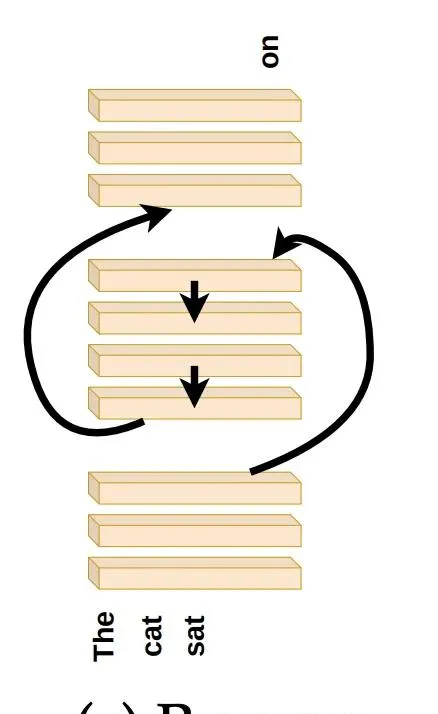
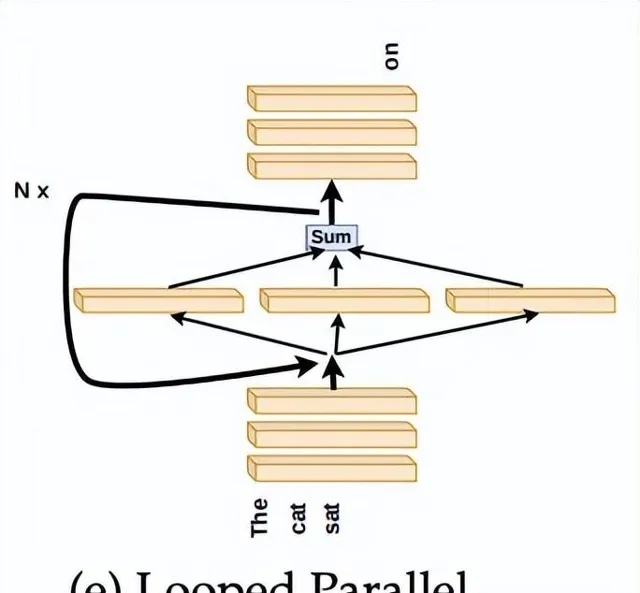
如果層的存在,即沒有被跳過,比它們執行的順序更重要,那麽是否可以考慮獨立地執行這些層,然後將它們的結果合並
?如下圖所示。
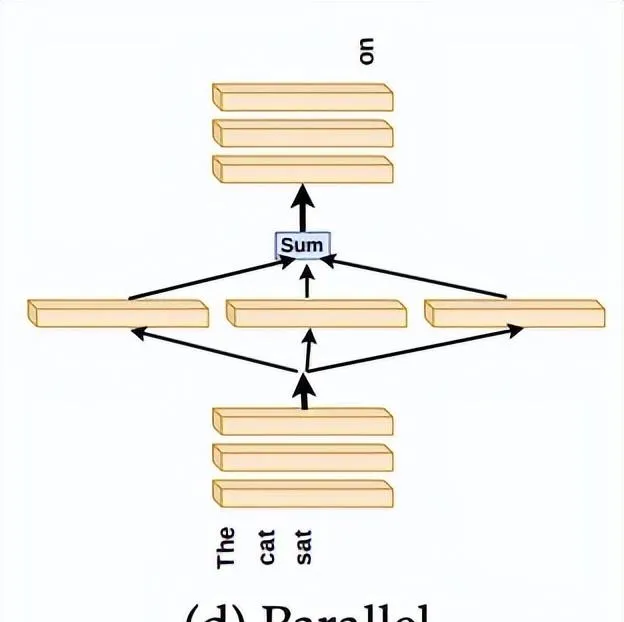
研究人員進行了一個實驗,不是跳過第N到第T-N層,而是並列執行這些中間層,然後將它們的平均結果傳遞到最後的N層。
結果如下圖所示,除了GSM8K數學題基準外,所有基準測試都表現出緩慢的效能退化。
有趣的是,並列層的表現優於跳過層,但不如逆序執行層。
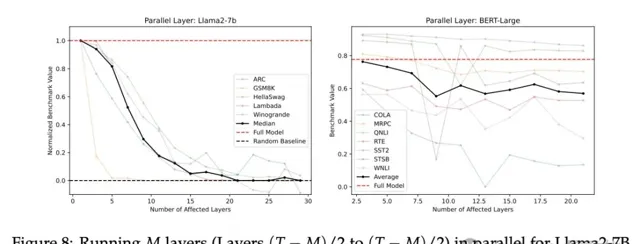
總之,可以並列執行這些層嗎?答案是:可以,數學為主的基準測試除外。
對於某些任務,順序是否更重要?
大多數變體(包括逆序、跳過和並列)在抽象推理ARC或數學推理GSM8K基準中,表現出最快速的效能下降。
可以解釋為逐步推理任務比「語意」任務(如Winogrande或HellaSwag)對層順序的變化更為敏感。
這是因為推理任務需要結合結構和語意雙重資訊,而HellaSwag這類任務僅需語意即可完成。
透過實驗,研究人員得出結論:數學和推理任務比「語意」任務更依賴順序。
叠代對並列層有幫助嗎?
如果把Transformer內部執行機制比作是畫一幅畫的過程:畫布(輸入)在一些畫家之間傳遞,一些畫家專門畫鳥,一些則更擅長畫輪子……每個畫家都依次從另一位畫家手裏接過畫布,然後決定對這幅畫進行補充,還是將其直接傳遞給下一位畫家(使用殘留誤差連線)。
可以想象,某些層在收到適當的輸入時才會對畫作進行「補充」。例如,如果「畫輪子」的畫家先看到汽車的車身,才更有可能畫上輪子。
在Transformer中,某些層可能只有在接收到適當的輸入時才會對前向傳遞發揮作用,而不是透過殘留誤差連線將輸入直接傳遞出去。
這麽來看的話,那麽相比於僅執行一次並列層,叠代執行並列層
應該會提高效能。
研究人員透過將並列層的平均輸出回饋到同一層並固定叠代次數來進行測試,如下圖:
下圖9中,研究人員展示了並列層叠代3次的結果,這種方法顯著優於僅執行一次並列層。
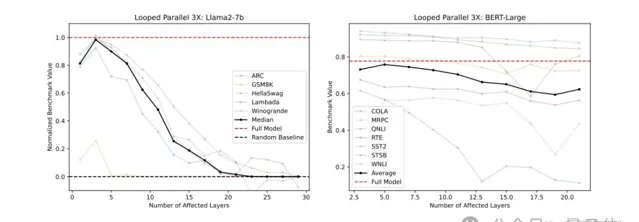
唯一的例外是在Llama2-7B的起始層N為15或BERT的起始層N為11時。在這種情況下,迴圈並列3次的效果相當於僅重復中間層3次,此時的並列層等同於完整模型。
研究人員還用不同的叠代次數重復進行了實驗。
下圖展示了Llama2-7B的效能隨並列層數M和叠代次數的變化而變化。
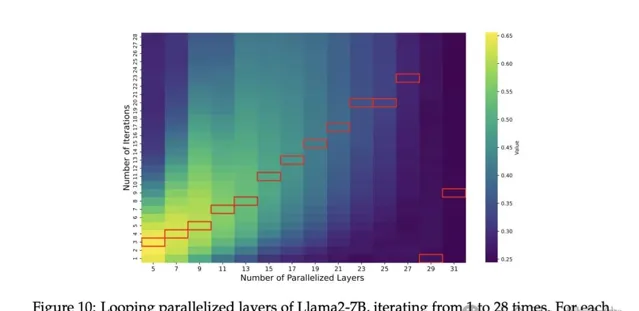
每個M的最佳叠代次數用紅框表示。除了M=29和M=31(幾乎並列所有層)外,最佳叠代次數大致與並列層數成線性比例。
因此結論是:叠代對並列層有幫助,最佳叠代次數與並列層數成比例。
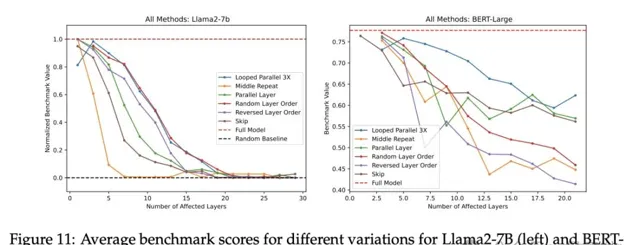
哪些變體對效能損害最小?
最後,研究人員將實驗中的所有不同變體在同一圖表上進行了比較。
結果顯示,重復單一層
(如上面提到的用同等數量的最中心的層替換中間層)效果最差
,效能迅速退化至隨機基準線。
叠代並列和隨機層順序效能退化最小
,其中叠代並列在BERT和Llama2-7B中表現最好。
論文附錄中還補充了更多實驗結果,感興趣的家人們可以檢視原論文。
論文連結:https://arxiv.org/abs/2407.09298v1
參考連結:https://x.com/A_K_Nain/status/1812684597248831912











