時間序列分析中包含了許多復雜的數學公式,它們往往難以留存於記憶之中。為了更好地掌握這些內容,本文將整理並總結時間序列分析中的一些核心概念,如自共變異數、自相關和平穩性等,並透過Python實作和圖形化展示這些概念,使其更加直觀易懂。希望透過這篇文章幫助大家更清楚地理解時間序列分析的基礎框架和關鍵點。
1、什麽是時間序列?-自共變異數、自相關和平穩性
時間序列與時間有關,隨著時間的推移觀察到的數據稱為時間序列數據:例如,心率監測,每日最高溫度等。雖然這些例子是有規律的間隔觀察到的,但也有不規則間隔觀察到的時間序列數據,如盤中股票交易、臨床試驗等。我們將使用定期觀察跨度的時間序列數據,並且只有一個變量(單變量時間序列)。從數學上我們可以這樣定義時間序列:
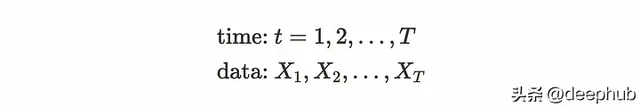
如果我們把X _l看作一個隨機變量,可以定義一個依賴於觀測時間t的均值和變異數。
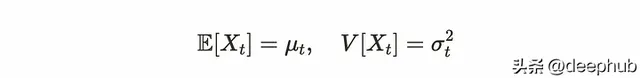
對於時間序列數據,可能想要比較過去和當前的數據。所以就引出了兩個基本概念,自共變異數和自相關
自共變異數
從技術上講,自共變異數和共變異數是一樣的。共變異數有如下公式:
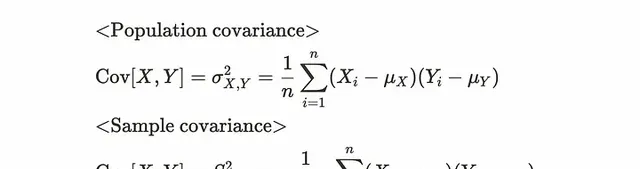
共變異數計算兩個變量X和y之間的關系。在計算樣本共變異數時,我們將每個觀測值與平均值之間的差除以n-1,類似於樣本變異數。對於自共變異數則計算前一個觀測值與當前觀測值之間的樣本共變異數。公式如下:
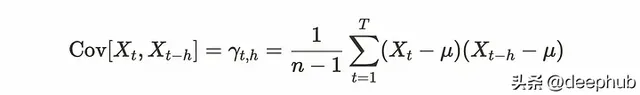
這裏的h被稱為滯後。滯後的X是前一個X值偏移了h位置。所以公式與共變異數相同。
自相關
自相關也和相關一樣,相關關系有如下公式。
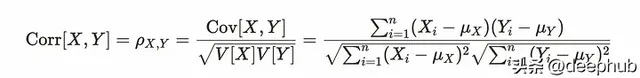
相關性將共變異數除以變量X和y的標準差,我們可以認為相關性類似於標準化共變異數除以標準差。對於自相關,計算以前和當前觀測值之間的相關性。h在公式中也表示滯後性。
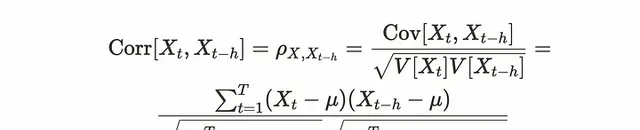
當共變異數和相關取較大的正值時,X和Y兩個變量呈正相關關系。那麽自共變異數和自相關呢?我們來看看視覺化。
對於第一個範例,從AR(1)流程生成數據(稍後我們將看到它)。它看起來像嘈雜的數據。

在這種情況下,自共變異數和自相關圖如下圖所示。x軸表示滯後。
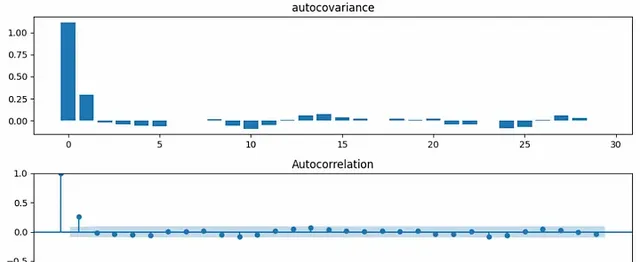
可以看到自共變異數和自相關有相似的趨勢。因此可以想象自相關可以被認為是標準化的自共變異數。
對於下面的範例將使用真實世界的數據,例如AirPassengers[4]。airpassenger數據有明顯的上升趨勢。
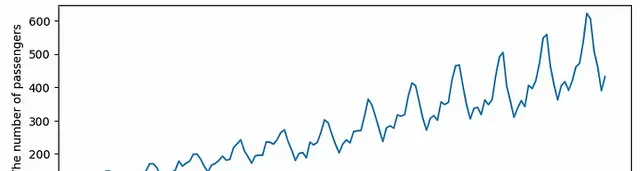
自共變異數和自相關圖如下圖所示。x軸表示滯後。
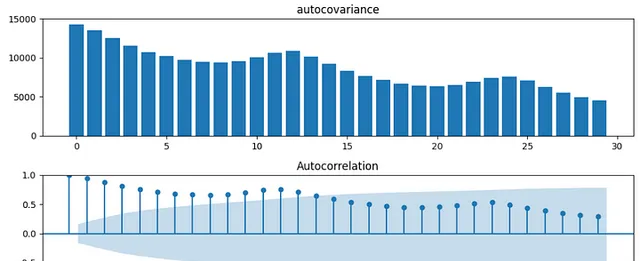
自共變異數和自相關也有類似的趨勢。這個數據比第一個例子有更多的相關性和更大的滯後。
我們了解了兩個關鍵概念,自共變異數和自相關。接下來,我們討論一個叫做平穩性的新概念。平穩時間序列意味著數據內容,如均值、變異數和共變異數,不依賴於觀測時間。平穩性有兩種類別:
弱平穩(二階平穩)
該過程具有以下關系,稱為弱平穩性,二階平穩性或共變異數平穩性。(有很多稱呼它的方式。)
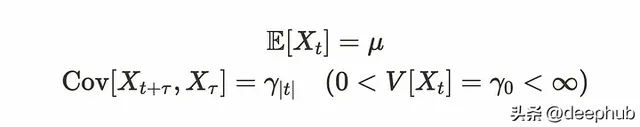
其中µ是常數,且 ₜ 不依賴於。這些公式表明,隨著時間的推移,均值和變異數是穩定的,共變異數取決於時滯。例如,上一段中的第一個例子具有弱平穩性。
嚴格平穩性(強平穩性)
令Fx()表示聯合密度函數時,嚴格平穩性描述為:
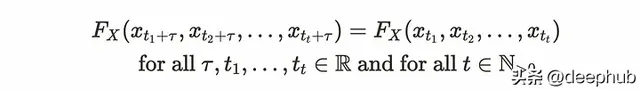
如果所有時間序列數據的聯合分布不隨時間的變化而變化,則該時間序列具有嚴格的平穩性。嚴格平穩意味著弱平穩。這個性質在現實世界中是非常受限的。因此許多應用程式依賴於弱平穩性。
有一些統計檢驗來檢驗時間序列數據是否平穩,我們後面進行介紹
2、時間序列過程
我們將介紹代表性的時間序列過程,如白雜訊、自回歸(AR)、移動平均(MA)、ARMA和ARIMA過程。
白雜訊
當我們擁有具有以下內容的時間序列數據時,該時間序列數據具有白雜訊。
白雜訊的均值為零,其變異數在時間步長上是相同的。它具有零共變異數,這意味著時間序列與其滯後版本是不相關的。所以自相關也是零。一般用於時間序列回歸分析中殘留誤差項滿足的假設。白雜訊圖如下圖所示。
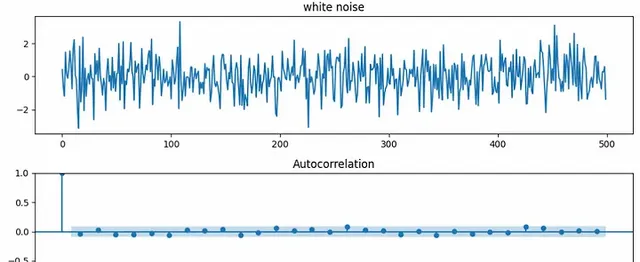
我們可以很容易地從標準正態分布中抽樣產生白雜訊序列。正如你所看到的,除了滯後0之外,似乎沒有任何相關性,隨著時間的推移,變異數似乎幾乎相同,平均值似乎為零。
自回歸(AR)的過程
一些時間序列數據的值與前面步驟的值相似。在這種情況下,自回歸(AR)過程可以很好地解釋數據。AR過程有一個表示序列中先前值的數量的順序,該順序用於預測當前值。我們用AR(order)表示。下式表示AR(1)過程。

Uₜ假定為白雜訊,來說是一個未知參數對應於一步前一個值。它也被稱為shock。當我們沿著前面的步驟解(1)式時,可以得到下面的公式。
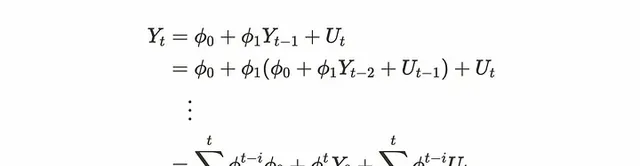
由上式可知,ᵗ₁僅影響Y系列。由此,可以認識到以下幾點:
如果| ₁ | < 1,則過去值的影響隨著步驟的增加而變小。
如果| ₁| = 1,無論滯後與否,過去值的影響是恒定的。
如果| ₁| > 1,則隨著步驟的推移,過去值的影響會影響當前值。
讓我們看看每種情況的視覺化。
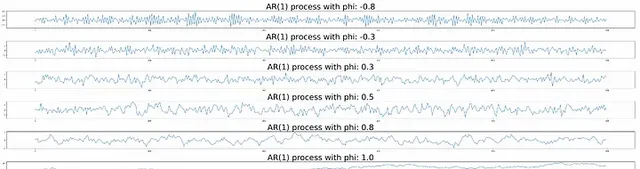
隨著₁值變大,當前一級跟隨前一級的值隨著值的增加,它看起來更平滑,直到₁ = 1。當₁值大於1時,這些值會像無窮大一樣增加,所以序列看起來像最終的結果。
註意:| ₁ | < 1的情況有弱平穩過程。當AR(1)過程滿足弱平穩性時,均值和共變異數為:
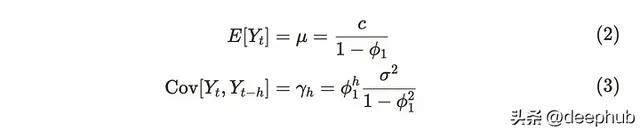
對於平均值,我們使用隨時間變化的平均值作為常數。利用白雜訊的平均值為零的事實,可以推匯出如下公式:
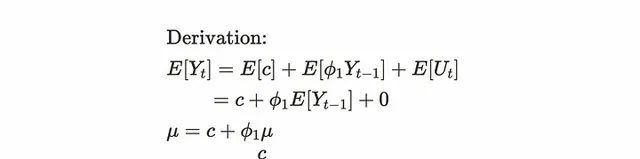
對於共變異數,我們需要先改變公式(1)
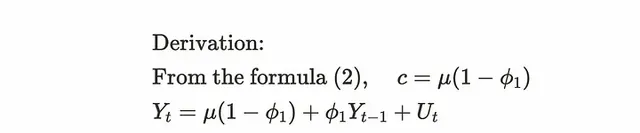
然後,按這個順序推導變異數和共變異數。對於變異數,可以透過對上述推導公式取平方來推導。
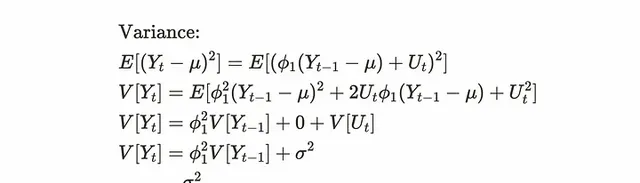
對於共變異數,可以透過將前一步值減去平均值來推導。
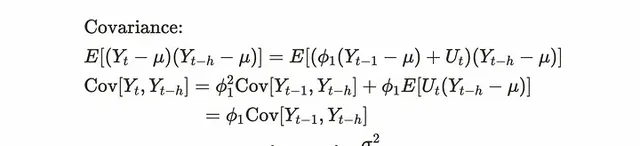
可以類似地考慮AR(p)過程。
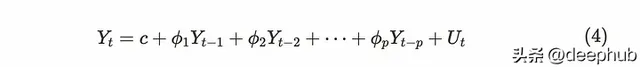
一般情況下,當滿足(5)(6)條件時,AR(p)過程是弱平穩的。
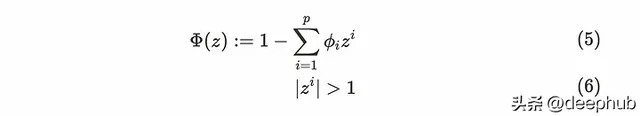
公式(5)和(6)意味著所有的根公式(5)必須在單位圓之外。盡管我們可以擴充套件p值,但在現實世界中先考慮幾個步驟就足夠了。
2、移動平均線(MA)過程
移動平均線(MA)過程由當前和以前的shock的總和組成。MA過程有一個表示先前殘留誤差或shock(Uₜ)的數量的順序。我們用MA(階)來表示。為簡單起見,我們介紹MA(1)流程。下式表示MA(1)過程。
假設U₁為白雜訊,θ₁為未知參數,對應前一步shock。MA(1)過程由白雜訊組成,其均值始終為µ。另一方面,變異數和共變異數可以推導為:
可以推匯出變異數如下:
同樣可以推匯出共變異數如下:
白雜訊假設每個變量是相互獨立的,所以可以消去它們。因此對於任意參數θ₁,MA(1)過程都是弱平穩過程。現在用視覺化的方法來驗證一下。
與AR(1)過程相比,均值和變異數似乎保持不變。隨著參數值的增大,序列變得相對平滑。註意MA(1)過程和白雜訊變異數不同。
一般來說,MA(q)過程也是弱平穩的。
均值和共變異數可以表示為:
盡管我們可以擴充套件q值,但考慮現實世界中的前幾個步驟就足夠了。
3、自回歸移動平均(ARMA)過程和ARIMA過程
顧名思義,自回歸移動平均(ARMA)過程結合了AR和MA過程。直觀上,ARMA過程可以相互彌補缺點,在表示數據時獲得更大的靈活性。數學表示如下:
我們將ARMA過程記為ARMA(p, q),參數p和q對應於AR和MA過程的參數。由於MA過程總是具有弱平穩性,因此ARMA過程的弱平穩性取決於AR部份。所以式(14)的AR部份滿足式(5)(6),其平穩性較弱。
透過視覺化來檢查它是如何看起來像ARMA過程的。AR(p=1,q=1)過程如下:
AR(p=3, q=2)過程如下圖所示。
可以看到它可以比單獨的AR和MA過程更好地掌握更復雜的數據結構。參數值越大,圖形越平滑。
最後自回歸積分移動平均(ARIMA)過程與ARMA過程有一些共同之處。不同之處在於ARIMA有一個積分部份(I),積分部份是指為了獲得平穩性需要對數據進行差分的次數。
首先,我們定義差分算子∇:
當想要更多的差分時,可以透過叠代將其擴充套件到冪:
使用差分參數,可以將ARIMA(p, d, q)過程定義為:
p為AR過程的階數,d為待微分的次數,q為MA過程的階數。在對數據進行區分之後,ARIMA過程就變成了ARMA過程。當時間序列的平均值不同時,ARIMA過程是有用的,這意味著時間序列不是平穩的。我們這裏使用的是AirPassengers數據集。因為不是所有序列的均值都相同,當我們對這個系列套用nabla時,圖形看起來如下所示:
與左圖的原始數據相比,右圖的平均值在時間序列中似乎是穩定的。
還有最後一個問題,我們想要在微分後擬合ARMA過程,如何定義參數?
有一些方法來確定它們如下。
用自相關函數(ACF)圖確定MA過程的階數(q),用部份自相關函數(PACF)圖確定AR過程的階數(p),或使用AIC或BIC來確定最佳擬合參數。
第一種方法,我們使用ACF和PACF圖來確定MA和AR過程的順序。PACF也是自相關的,但是在0 < n < k的範圍內,消除了滯後n的Y′′和Y′′+ₖ之間的間接相關關系。我們有時不能僅用圖來確定參數,所以使用第二種方法。AIC和BIC是用來估計相對於其他模型的模型質素的資訊標準。借助庫pmdarima[7],可以很容易地根據上述資訊標準找到最佳參數。例如,當使用pmdarima來估計AirPassengers數據時,結果將如下所示。
# fit stepwise auto-ARIMA
arima = pm.auto_arima(y_train, start_p=1, start_q=1,
max_p=3, max_q=3, # m=12,
seasonal=False,
d=d, trace=True,
error_action='ignore', # don't want to know if an order does not work
suppress_warnings=True, # don't want convergence warnings
stepwise=True) # set to stepwise
arima.summary()
只需寫幾行程式碼,就可以很好地擬合和預測數據。此外pmdarima可以使用更高級的模型(如SARIMA)來估計時間序列。所以pmdarima在實際用例中非常有用。
3、時間序列的統計檢驗
最後我門將介紹兩個著名的時間序列統計檢驗。這些檢驗通常用於檢查數據是否平穩或殘留誤差項是否具有自相關。在深入每個測試之前,有一個重要的概念叫做單位根。如果時間序列有單位根,它就不是平穩的。如果AR(p)過程滿足式(5)= 1的至少一個根,這意味著AR(p)過程不是平穩的,所以可以說AR(p)過程具有單位根的。有幾個統計測試使用了這個概念。
增強Dickey-Fuller(ADF)檢驗
增強的Dickey-Fuller (ADF)檢驗評估在給定的單變量時間序列中是否存在單位根。
ADF檢驗采用由式(10)匯出的下式。
然後,它設定以下零假設和備擇假設。
統計數據如下公式所示。
當時間序列平穩時,分子必須為負。有幾個庫允許我們計算ADF測試,因此不需要自己實作它們。下面的範例顯示了三個時間序列數據範例。左邊的是AR(1)過程,中間的是MA(1)過程,最後一個是AirPassenger數據集。圖示題顯示ADF檢驗的行程名和p值。
平穩數據(左和中)小於閾值的顯著性,因此我們可以拒絕零假設,這意味著數據是平穩的。非平穩數據(右)比閾值更大,所以我們不能拒絕零假設,這意味著數據不是平穩的。
Durbin-Watson檢驗
Durbin-Watson檢驗用於評價時間序列回歸模型中殘留誤差項是否具有自相關性。當我們使用時間序列假設以下回歸模型時,我們可以使用最小平方法估計參數。
如果Uₜ不遵循白雜訊,模型質素就不好。可以考慮Uₜ具有某種自相關或序列相關,我們應該將它們包含在我們的模型中。為了驗證這一點,我們可以使用Durbin-Watson測試。Durbin-Watson檢驗假設殘留誤差項具有AR(1)模型。
然後設定以下零假設和備擇假設。
我們使用下面的統計。
這個公式可能不太直觀,所以我們把它改一下。我們假設T對於下面的關系足夠大。
我們將Durbin-Watson統計量變換為:
表示一階自相關。當自相關趨近於0時,DW統計量趨近於2,這意味著時間序列中幾乎沒有自相關。如果時間序列中存在自相關,則DW統計量小於2。
讓我們使用在2.4節中建立的ARIMA模型檢查DW統計量。
from statsmodels.stats.stattools import durbin_watson
arima = pm.arima.ARIMA(order=(2,1,2))
arima.fit(y_train)
dw = durbin_watson(arima.resid())
print('DW statistic: ', dw)
# DW statistic: 1.6882339836228373
DW統計量小於2,因此仍然存在自相關或序列相關。下面的殘留誤差圖顯示殘留誤差仍然有一定的相關性。
在這種情況下,我們需要使用更高級的模型來正確擬合數據。例如SARIMA,迴圈神經網絡,prophets等。
參照
[1] 統計検定準一級
[2] Wang, D., Lecture Notes, University of South Carolina
[3] Buteikis, A., 02 Stationary time series
[4] AirPassengers dataset, kaggle
[5] Eshel, G., The Yule Walker Equations for the AR coefficients
[6] Bartlett, P., Introduction to Time Series Analysis. Lecture 12, Berkeley university
[7] pmdarima: ARIMA estimators for Python
作者:Yuki Shizuya











