大家好,今天要讲的内容是,误差反向传播算法。
误差反向传播算法,是神经网络中的学习难点。
而理解误差反向传播算法,是理解神经网络模型训练过程的关键一环。
希望这个篇文章,能帮助同学们,彻底弄懂误差反向传播算法。
1.误差反向传播有什么用
神经网络的训练目标,是最小化网络的代价函数E。
为了找到使E取得最小值时的参数值,会使用梯度下降算法。
而运行梯度下降算法,就需要计算出E关于网络中各个参数w和b的偏导数:
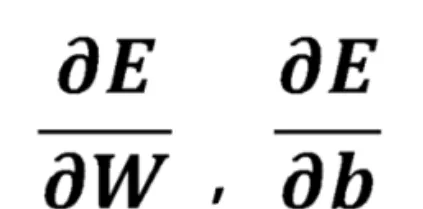
误差反向传播算法,基于链式法则,将E关于参数的偏导数计算,分解为一系列简单的步骤:

误差反向传播从输出层开始,逐层的向前计算E关于各层之间参数的偏导数,最后到达输入层。
由于这个过程是从后向前的,因此它被称为「反向传播算法」。
误差反向传播算法,有一个通用的公式:
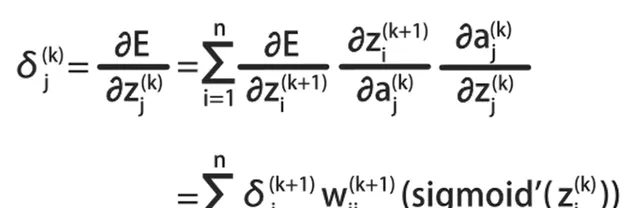
根据这个公式,可以计算E关于各层之间参数的偏导数:
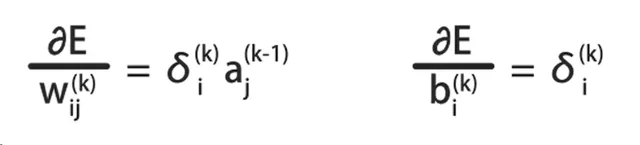
它是误差反向传播算法的核心公式。
今天我们不讨论这个公式的推导,而是使用一个具体的三层神经网络:

举例说明误差反向传播的计算过程。
这里会具体的计算出,E关于w1到w8,E关于b1到b4的偏导数:
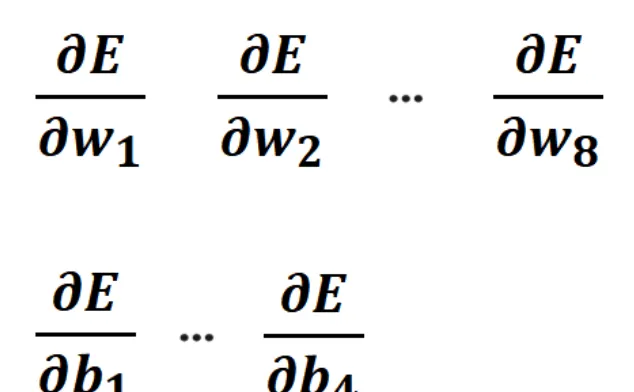
有了这些偏导数,就可以对这个神经网络,运行梯度下降算法了。
2.神经网络的前向传播
为了说明反向传播算法,需要先弄明白,神经网络前向传播的计算过程。
在这个过程中,我们将使用计算图来详细说明这个神经网络。
在样例神经网络中,使用sigmoid激活函数和交叉熵误差E:

其中x1和x2是输入的特征值。
a1和a2是第2层神经元的输出。
p1和p2是第三层的输出。
另外,使用w1到w8表示8个w参数。
b1到b4表示4个偏置参数。
z1到z4表示4组线性累加和的结果。
3.画出神经网络的计算图
首先画出输入层到隐藏层的前向传播计算图:
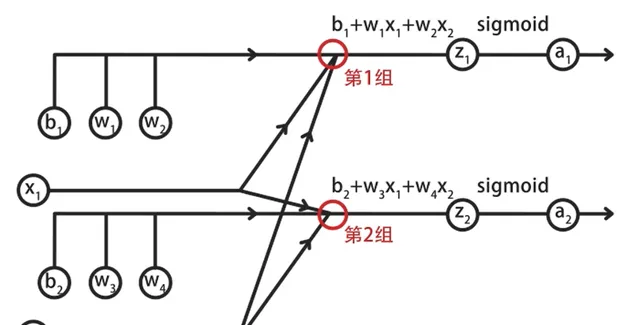
其中包括了两组线性方程求和,与sigmoid函数计算。
具体来说,在第一组计算中,输入层的两个特征x1和x2对应参数w1和w2。
将它们相乘后,再加上偏置b1等于z1,将z1代入到sigmoid中,得到a1。
按照同样的方式,计算第2组的输出。
其中,z2=x1*w3+x2*w4+b2,a2=sigmoid(z2)。
这样就完成了输入层到隐藏层的计算,结果是a1和a2。
然后画出隐藏层到输出层的前向传播计算图,其中同样包括两组计算:
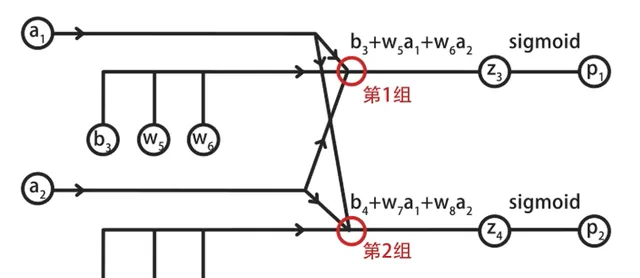
在第一组计算中,输入的a1和a2与参数w5和w6相乘,再加上偏置b3,得到z3。
将z3代入到sigmoid,得到输出层第1个神经元的输出p1。
同理,可以计算出第2组的结果p2。
我们将这两组计算图合并,就得到了神经网络前向传播的完整计算图:
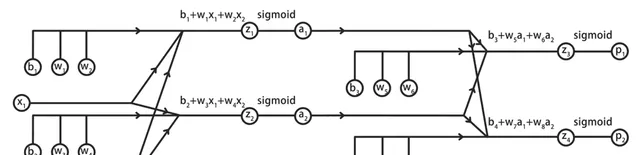
为了计算误差E关于参数的偏导数,还需要将E加到计算图中:
这里我们只关注某一个样本产生的误差E,从而忽略掉西格玛求和符号。
在输出层中,包括两个神经元,它们的人工标记结果是y1和y2,神经网络的输出结果是p1和p2。
根据交叉熵误差,分别计算两个神经元的误差,为E1和E2,总误差E=E1+E2。
这样,我们就得到了这个三层神经网络的完整计算图:
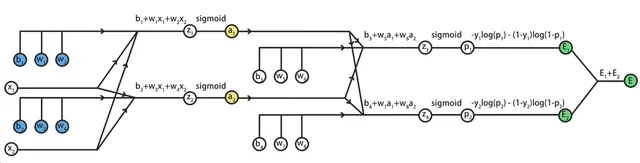
接下来,我们要根据这个计算图,使用链式法则。
从后向前,推导出代价函数E,关于参数w1到w8、b1到b4的偏导数。
这实际上,就是反向传播算法的手动计算过程。
4.误差发现传播算法
先来研究神经网络的后半段,也就是w5、6、7、8对整体误差E产生的影响。
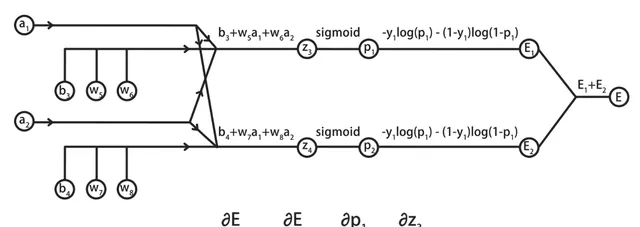
具体以w5为例,说明E关于w5的偏导数的计算过程。
在计算时,需要基于链式法则,将E关于w5的偏导数,拆解为E对p1、乘p1对z3、乘z3对w5的偏导数。
5.E关于w5偏导数的详细计算过程
首先计算E对p1的偏导数:

在计算时,需要基于log函数的求导方法,计算结果为-y1/p1+(1-y1)/(1-p1),其中y1是常数。
然后计算p1对z3的偏导数:

在计算时,需要基于sigmoid函数的求导:

设g(z)为sigmoid函数,g(z)的导数为g(z)*(1-g(z))。
p1=sigmoid(z3),因此p1对z3的偏导数,就是p1*(1-p1)。
最后基于线性方程,计算z3对w5的偏导数:
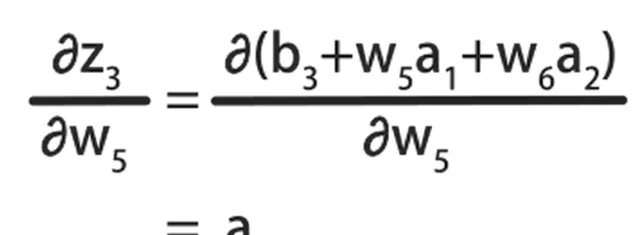
它等于w5的系数a1。
将三组计算结果相乘,消去重复的项,就得到了E对于w5的偏导数:
它等于神经元的输出值p1减标记值y1乘对应的输入特征a1。
仔细观察可以发现,这个结果与逻辑回归中的梯度计算结果是一样的。
按照同样的方式,可以计算出E对w6、w7、w8和b3、b4的偏导数:
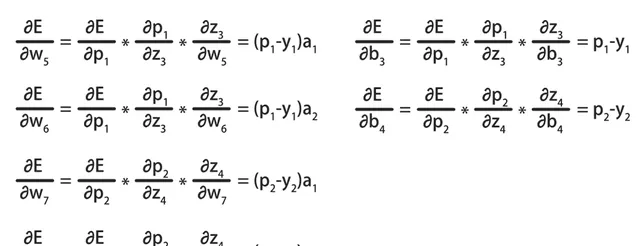
这种基于链式法则,从后向前计算偏导数的方式,就被称为向后传播算法。
接下来,我们继续推导E对于w1到w4,b1和b2的偏导数。
观察计算图的前半部分:
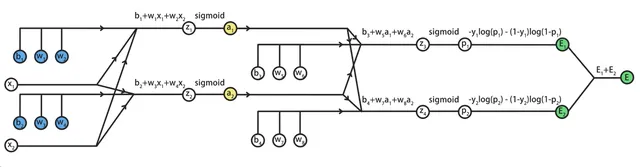
可以发现蓝色标记的待求参数,会经过a1和a2,再传导到E。
因此,如果可以先求出E对a1和a2的偏导数,再基于链式法则,就能推导出E关于蓝色参数的偏导数了。
6.E关于a1和a2的偏导数计算
在求E关于a1、a2的偏导数时,会发现z3、z4同时出现在a1、a2到E的路径上:

这说明a1和a2与z3和z4都是有关系的。
因此我们需要先求出E对z3、z4的偏导数。
再求z3、z4对a1、a2的偏导数,最后合并到一起,得到结果。
我们将中间不相关的变量节点全部省略掉,得到了一个更简单的计算图:
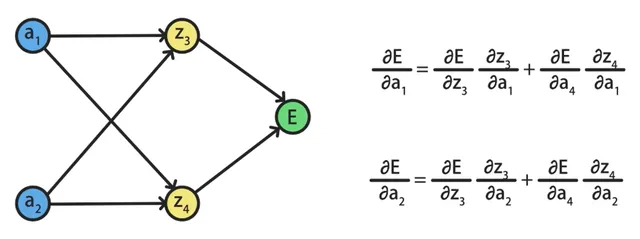
其中E对a1的偏导数,可以基于a1、z3、E和a1、z4、E两条路径计算。
而E对a2的偏导数,可以基于a2、z3、E和a2、z4、E两条路径计算。
我们已经推导出E关于z3、z4的偏导数,它等于神经元的输出值p减去该输出对应的标记值y:

另外,z3和z4对于a1的偏导数,是a1的系数w5和w7。
z3和z4对于a2的偏导数,是a2的系数w6和w8。
求出链式法则需要的中间结果后,将它们代入到E关于a1和a2的偏导数公式中,就得到了最终的结果:
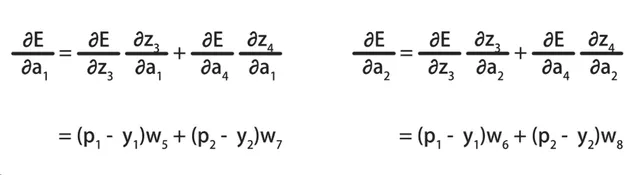
有了E关于a1和a2的偏导数后,就可以继续通过链式法则,求出E关于参数w1到w4、b1和b2的偏导数了。
我们以E关于参数w1的偏导数,来说明计算过程:
根据链式法则,E对w1的偏导数,等于E对a1、a1对z1、z1对w1这三个偏导数结果的乘积。
其中E对a1的偏导数,已经求出,a1对z1是sigmoid函数求导。
而z1对w1求导,是w1对应的特征x1:
将这三个值相乘,就得到了E对w1偏导数的具体值了:
按照同样的方法,可以继续求出E对于w2、w3、w4和b1、b2的偏导数。
这样我们就使用误差反向传播算法,将E关于神经网络中所有参数的偏导数,都求出来了。
后面可以直接使用这些偏导数,进行梯度下降算法的迭代。
那么到这里,误差反向传播算法就讲完了,感谢大家的观看,我们下节课再会。











