当我们深入研究数学猜想时,卡塔兰猜想就像一个等待破解的诱人谜团一样吸引着我们。就像一个被一个令人困惑的案件吸引的侦探一样,我发现自己无法抗拒地被这个有趣的命题所吸引。
该猜想由比利时数学家 Eugène Charles Catalan 于 1844 年首次提出,其神秘性近两个世纪以来一直吸引着数学家的注意力。其本质在于一个看似简单的问题:除了 8 和 9 之外,自然数的连续幂对是否只有有限对?
当我思考这个问题时,我被它看似简单的外表所震惊。乍一看,它似乎很简单 ——只是探索整数幂之间的关系。然而,在这简单的外表之下隐藏着一个错综复杂的数学关系迷宫,等待我们去揭开。
我对卡塔兰猜想的深入探究,让我穿越了质因数分解、模数运算和丢番图方程的领域。每走一步,我都会感受到数学推理的优雅和数值模式的优美。
然而,尽管经过了几个世纪的探索,卡塔兰猜想仍然悬而未决。它证明了数学的无限复杂性,挑战我们突破理解的界限,直面数学宇宙核心的奥秘。
当我继续探索卡塔兰猜想时,我想起了法国数学家亨利 ·庞加莱的话:「数学就是给不同事物赋予相同名称的艺术。」
数字的力量
卡塔兰猜想,又称米海列斯库定理,是数论中一个引人入胜的成果。它由数学家尤金 ·查尔斯·卡塔兰于 1844 年首次提出,一个多世纪以来一直是个有趣的悬而未决的问题,直到 2002 年罗马尼亚数学家普雷达·米海列斯库终于解决了它。
卡塔兰猜想
该猜想涉及强大数学概念之间的迷人相互作用,对于理解某些指数方程的整数解的结构具有深远的影响。

考虑大于
1 的整数的平方和立方序列,从整数 4、8、9、16、25、27、32 和 36 开始……
值得注意的是,在这个数列中,两个连续项不仅是整数的完全幂,而且也是连续的整数。例如,
8(即 2 的立方 23)和 9(即 32,即 3 的平方 32)既是连续的整数,也是整数的幂。
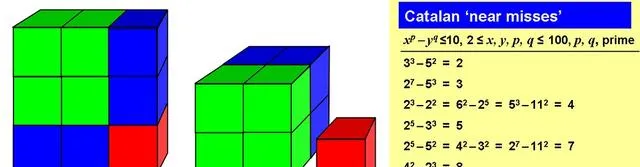
在这里,我们可以看到对之间的差异增加了。因此,除了对 (8,9) 之外,我们不可能得到等于 1 的差异。
寻求解决方案
卡塔兰猜想的表述 看似简单 ——如果「a」和「b」是大于 1 的正整数,并且是互质数(即它们没有除 1 之外的共同因子),并且它们不是完全平方数,那么存在等式
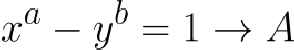
它在正整数 x、y、a 和 b 中只有一个解,即 a = 2 和 b = 3,其中 x = 3 和 y = 2。这意味着除了众所周知的对 ( ³² — ²³ = 1 ) 之外,没有其他相差为 1 的连续正整数幂对。
为了解这个方程,
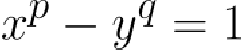
在这里,因式分解使问题变得容易得多,因为我们现在可以专注于理解 y 的除数。假设 y 是奇数,这意味着 2 不能整除 y。
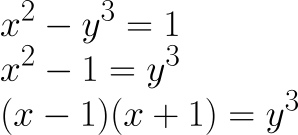
如果
y 为奇数,则 y 的任何因数要么整除 (x — 1),要么整除 (x + 1),但不能同时整除两者。这意味着 (x — 1) 和 (x + 1) 都必须是立方数,因为 y 的所有因数都必须包含在这两个项之一中。
但是,我们知道两个立方体之间的距离不可能只有两个。想想立方体数字的序列 ——1、8、27 等等。每次,我们都在增加更多,对吧?因此,随着我们沿着这个序列移动,任何两个连续立方体之间的差异都会越来越大。这就是为什么你找不到两个相差两个单位的立方体。
假设我们有这个方程。如果 y 是奇数,那么,结果就是没有可行的答案。现在,如果 y 是偶数,似乎会给我们一些额外的回旋余地,因为 2 是因数。但是,信不信由你,同样的想法也适用,在这种情况下你仍然找不到任何解决方案。
Preda Mihăilescu 在数论方面的胜利
这个猜想背后的想法看似简单,但证明它却并非易事。它被认为是 21 世纪数论领域的重大里程碑之一。Preda Mihăilescu 的证明?嗯,他就像是把代数数论中的所有重炮都拿出来了。他深入研究了诸如圆域和伽罗瓦表示之类的东西,相信我,这些都不是轻松就能理解的。他的策略的核心是什么?他深入研究了所谓的 Wieferich 素数,并使用了伽罗瓦模块结构和模形式理论中一些非常复杂的东西。
为了理解卡塔兰猜想的特别之处,让我们回顾一下过去,看看它是如何融入大局的。我们有一位名叫尤金 ·查尔斯·卡塔兰的人,他是一位来自比利时、拥有法国血统的数学天才。这家伙在数学方面毫不逊色——他在组合学、几何学和数论等各种领域都引起了轰动。
因此,早在 1844 年,卡塔兰就给他的数学伙伴约瑟夫·伯特兰写了一封信,信中他脑子里浮现出这个想法。他说:「嘿,如果我抛出这个大胆的猜测会怎么样?」这就是整个事情的开始。
一百多年来,世界各地的数学天才们就像侦探一样试图破解这个数学谜题 ——卡塔兰猜想。他们用尽了书上的所有技巧来证明它是正确的还是错误的。在这一过程中,他们取得了一些真正的进展,解决了一些案例,并想出了各种巧妙的方法。但问题是——他们无法把整个谜题拼凑起来。
然后,德国数学大师保罗 ·沃尔夫斯凯尔 (Paul Wolfskehl) 出现了。他对整个加泰罗尼亚猜想非常感兴趣,以至于他在遗嘱中为任何最终能破解它的人提供了一大笔现金奖励。现在,尽管没有人最终获得该奖项,但它肯定让每个人都对这个问题感到兴奋。沃尔夫斯凯尔的提议点燃了研究人员的热情,促使他们全力以赴破解密码。
时间快进到 1985 年——这是卡塔兰猜想的真正转折点。想象一下,罗伯特·蒂德曼和莫里斯·米格诺特这两位数学奇才,各自工作,却都中了大奖——他们破解了方程 A 的密码。他们的发现意义重大——他们证明了,对于任何给定的指数「a」和「b」,这个方程只有有限数量的解。这就像发现了数学世界中隐藏的宝藏。
现在,他们并没有完美地揭开卡塔兰猜想的整个谜团,但这一被称为蒂德曼 -扎吉尔定理的发现是一个巨大的飞跃。它让我们得以一窥方程的内部运作,让我们走上了更好地理解它的道路。
2002 年,罗马尼亚数学家 Preda Mihăilescu 取得了突破性进展,证明了该猜想,并借鉴了众多前辈数学家的贡献。他的革命性证明发表在题为「基本循环单元和 Catalan 猜想的确认」的论文中。
米海列斯库的方法论融合了几个关键概念和方法论。其中,分圆域理论发挥了核心作用。这些域是通过添加单位根而获得的有理数域的扩展,提供了重要的见解。具体来说,米海列斯库利用分圆单元的特性和分圆域固有的伽罗瓦模块结构来仔细研究方程 A。
伽罗瓦模块表示受伽罗瓦群作用的模块。具体而言,它是指具有源自特定域扩展的伽罗瓦群的群作用的模块。术语 「伽罗瓦表示」在表示论中通常表示域上的向量空间或环上的自由模块时的伽罗瓦模块。不过,它也可以与「G 模块」互换使用,强调基本代数结构及其与伽罗瓦群作用的相互作用。
Preda Mihăilescu 证明中的 Wieferich 素数和模形式
证明的另一个关键部分集中在研究维费里希素数上。 Preda Mihailescu 于 2002 年 4 月 18 日完成了他的证明,首先证明除了 (p,q) = (2,3) 对之外,该问题的任何解都必须满足以下两个条件:
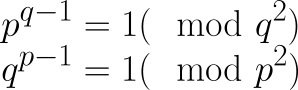
如果素数 p 的平方能被表达式 2^p -1–1 整除,则该素数为维弗里奇素数。(图片由作者提供)
P 是以 q 为底的维弗里奇素数,q 是以 p 为底的维弗里奇素数。
为了完成证明,米海列斯库使用了模形式理论的一个深刻结果,具体涉及模形式 Δ(z) — 1,其中 Δ(z) 是判别函数。
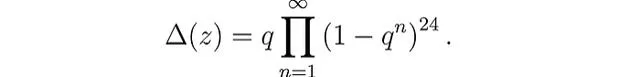
这使他能够确定,对于
「a」和「b」的特定条件,方程 A 没有其他解。
米海列斯库成功解决了卡塔兰猜想,赢得了数学家们的广泛赞誉。他优雅的证明为几代数学家着迷的问题提供了决定性的解决方案。此外,它还强调了数学界合作努力的有效性。多年来,众多数学家取得的累积进展为最终证明奠定了基础,凸显了集体努力在解决具有挑战性的数学问题方面的力量。
卡塔兰猜想的解决不仅解决了一个长期存在的问题,而且还深入了解了特定指数丢番图方程的正整数解的底层结构。米海伊列斯库的证明强调了数字 2 和 3 的重要性,将它们与维费里希素数的基本性质及其与模形式 Δ(z) — 1 的关系联系起来。
此外,米海列斯库的成就对各个数学领域都具有深远的影响。它与丢番图方程理论、模形式和圆分域探索等不同领域建立了联系。











