导语:线性代数作为一门思维的艺术,不仅仅局限于数学领域,而且渗透到了科学、工程、计算机科学乃至经济学和社会科学等多个领域。本文将详细介绍线性代数的基本概念和原理,并通过具体例子分析其在各领域中的应用,带您走进这门令人着迷的学科。

一、基本概念
线性代数是研究向量空间和线性变换的分支学科。它的基本概念包括向量、向量空间、线性变换和矩阵等。向量是有方向和大小的量,可以用来表示物理力、速度、加速度等;向量空间则是由向量构成的集合,具有一些特定的性质,如封闭性和线性组合性质;线性变换是指保持向量空间中线性组合关系的变换,常见的例子有旋转、缩放和投影等;矩阵则是将线性变换用矩阵形式表示的工具。

二、向量空间的结构化思维
向量空间的概念在科学和工程领域中具有广泛的应用。例如,在物理学中,我们可以利用向量空间的结构描述物体的运动状态,如位移、速度和加速度等。在电路分析中,向量空间可以用来描述电路网络的行为特性,如电流和电压的关系。化学反应的平衡状态求解也可以使用向量空间的概念。通过将问题转化为向量空间的形式,我们可以更好地理解问题的本质,并采用适当的数学方法进行求解。
三、线性变换的几何解释
线性变换是线性代数中的重要概念,它具有丰富的几何解释。例如,缩放可以看作是对向量进行拉伸或压缩;旋转可以看作是将向量绕某个固定点旋转一定角度;反射可以看作是将向量沿着某个轴翻转。这些几何变换在计算机图形学、机器学习和数据分析等领域中有着广泛的应用。通过分析线性变换的几何特性,我们可以更好地理解它们的作用,并将其应用于实际问题中。
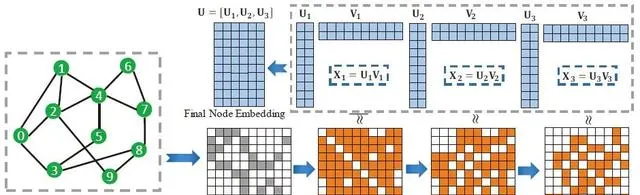
四、基本理论与问题分析
线性代数中的基本理论包括线性独立、基和维度的概念,以及向量空间的同构性等。线性独立是指向量组中不存在不必要的冗余信息,它在问题分析和解决中起到重要作用。基是向量空间的一组最小生成集,它可以用来表示向量空间中的任意向量。维度则是向量空间的基的个数,它反映了向量空间的维度大小。通过对这些基本理论的理解,我们可以更好地分析和推导问题,找到问题的解决方案。
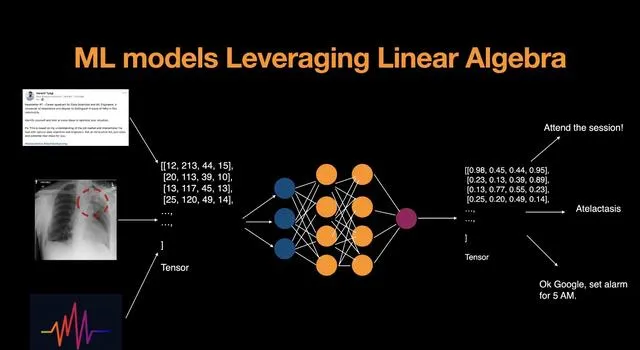
五、特征值与特征向量的动态特性
特征值和特征向量是线性变换中重要的概念,它们具有丰富的动态特性。特征值表示线性变换在某个方向上的特定缩放因子,特征向量则表示在该方向上的不变方向。在动力系统和稳定性分析中,特征值和特征向量可以帮助我们理解系统的动态行为和稳定性特性。在科学和工程领域中,特征值和特征向量的概念被广泛应用于描述振动系统、电路网络和物理模型等。
结语
线性代数是一门令人着迷的学科,它在多个领域中发挥着重要作用。通过本文的介绍和分析,希望读者能更好地理解线性代数的基本原理和应用,从而在实际问题中灵活运用这一强有力的工具。无论是科学、工程还是社会科学,线性代数都为我们提供了一种统一的语言和视角,帮助我们解决复杂问题,推动学科的发展。











