几何学,作为数学的古老分支,长久以来一直以其独特的视角探索着空间的奥秘。然而,它与物理学的交织,尤其是与广义相对论和弦论的关联,揭示了几何学在现代科学中的核心地位。本文旨在深入探讨几何学如何为物理学提供了关于宇宙结构的深刻见解,特别是通过卡拉比-丘流形的发现,我们如何得以一窥多维宇宙的神秘面纱。
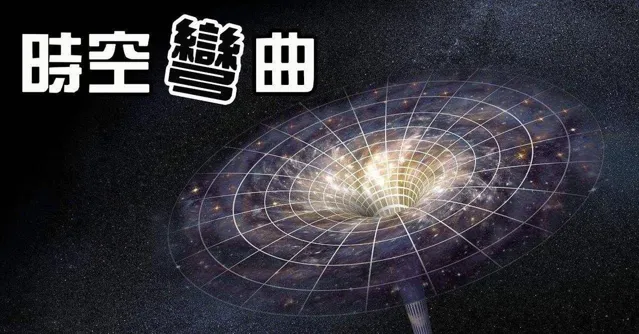
一、 爱因斯坦的广义相对论与几何学
爱因斯坦的广义相对论是20世纪物理学的一座里程碑。在1915年,爱因斯坦提出了一个革命性的理论,将引力视为由物质引起的时空弯曲。这一理论的核心在于,引力不再被看作是一种力,而是时空几何的一部分。爱因斯坦的这一理论,实际上是站在了19世纪数学巨匠高斯和黎曼的肩膀上。高斯的内蕴几何概念和黎曼对弯曲空间的研究,为爱因斯坦提供了描述时空曲率所需的数学语言。
1.1 几何学与引力的统一
在爱因斯坦的理论中,物质告诉时空如何弯曲,而时空的弯曲告诉物质如何运动。这一统一的视角,可以用数学公式表达为爱因斯坦场方程:
[ G_{\mu\nu} + \Lambda g_{\mu\nu} = \frac{8\pi G}{c^4} T_{\mu\nu} \]
其中,( G_{\mu\nu} ) 是爱因斯坦张量,代表了时空的几何性质;( Lambda ) 是宇宙常数,代表了宇宙的加速度;( g_{\mu\nu} ) 是度规张量,描述了时空的局部几何结构;( T_{\mu\nu} ) 是能量-动量张量,代表了物质和能量的分布;( G ) 是引力常数,( c ) 是光速。

1.2 卡拉比-丘流形的发现
丘成桐教授的工作,特别是在卡拉比-丘流形上的突破,为理解广义相对论中的某些特殊解提供了关键的数学基础。卡拉比-丘流形是一类特殊的紧致凯勒流形,它们在每个点上都有零里奇曲率。这一性质意味着,这些流形可以被视为广义相对论中的真空解,即不包含物质的时空解。
1.3 卡拉比猜想与丘成桐的工作
卡拉比在20世纪50年代提出了一个猜想,即是否存在一种几何结构,使得紧致流形的每个点上里奇曲率都为零。这一问题在数学上被称为卡拉比猜想。丘成桐在1976年证明了这一猜想,他的工作不仅解决了一个长期悬而未决的数学问题,而且为物理学家提供了一种全新的视角来探索宇宙的基本结构。

二、 弦论与多维宇宙
弦论是一种试图统一所有基本物理力的理论框架。在弦论中,基本的构成单元不再是点粒子,而是一维的「弦」。这些弦的振动模式决定了我们观察到的粒子和力的性质。为了自洽,弦论需要存在十个维度,但我们在日常生活中只能感知到四个维度(三个空间维度和一个时间维度)。
2.1 隐藏维度的几何解释
弦论提出了一个解释,即额外的六个维度被卷曲在一个极小的空间尺度上,这个尺度小到无法直接观测。卡拉比-丘流形提供了一个可能的几何结构,使得这些额外的维度可以被隐藏起来。这些流形的紧致性和零里奇曲率特性,使得它们成为弦论中隐藏维度的理想候选者。
本书从「零」开始,站在「问题」角度,循序渐进地讲述了整个物理学理论的演变过程,内容涵盖经典力学、电磁学、热力学与统计力学、光学、相对论、量子物理和宇宙学。本书思路清晰、行文流畅,措辞严谨又不乏幽默,插图简约又不乏精准,内容简练又不乏深意。除物理外,本书多处以开放式思维探讨物理与数学、哲学的关系,旨在与读者共同建立理性思维,是青少年及广大物理爱好者绝佳的入门书籍。

结论
几何学与物理学的相互作用,特别是在广义相对论和弦论中的应用,为我们提供了探索宇宙奥秘的新工具。卡拉比-丘流形的发现,不仅解决了一个深奥的数学问题,而且为物理学家提供了一个探索多维宇宙的新途径。尽管弦论仍有许多未解之谜,但其数学基础的坚实性和对数学领域的深远影响,预示着它可能包含着关于宇宙本质的深刻真理。
参考文献
1. Einstein, A. (1915). Die Feldgleichungen der Gravitation. *Königliche Preussische Akademie der Wissenschaften*. Berlin. 1915, 844–847.
2. Calabi, E. (1954). The space of Kähler metrics. *Proceedings of the International Congress of Mathematicians*, 150–152.
3. Yau, S.-T. (1977). Calabi's conjecture and some new results in algebraic geometry. *Proceedings of the National Academy of Sciences*, 74(5), 1798–1799.
4. Greene, B. (1999). *The Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory*. W. W. Norton & Company.
5. Strominger, A., & Yau, S.-T. (1986). Mirror symmetry is T-duality. *Nuclear Physics B*, 479(1-2), 243–259.











