通过前面的学习,我们知道了,定积分可以通过牛顿—莱布尼兹公式问题转换为线段两个端点的某个函数差。二重积分可以通过格林公式转换为积分区域边界线的曲线积分。三重积分可以通过高斯公式转换为积分区域边界面的曲面积分。
今天我们来学习联系曲线积分和曲面积分的—斯托克公式。
对坐标的曲线积分,如果曲线是空间曲线并且封闭,则它可张成一个曲面,可进行对坐标的曲面积分。两者就产生了联系,而联系它们的就是斯托克斯公式。
对坐标的曲线积分和曲面积分中,曲线和曲面都是有向的。建立曲线积分和曲面积分的关系之前,需要引入右手规则。
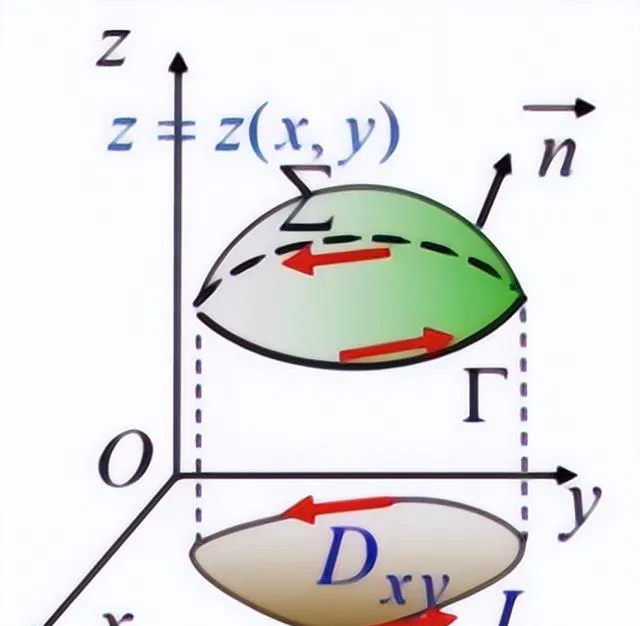
右手规则:设Γ是分段光滑的有向闭曲线,Σ是以Γ为边界的分片光滑的有向曲面。当右手除拇指外的四指依Γ的方向绕行时,拇指的指向与Σ的法线方向相同,则称Γ是有向曲面Σ的正向边界曲线。如下图:
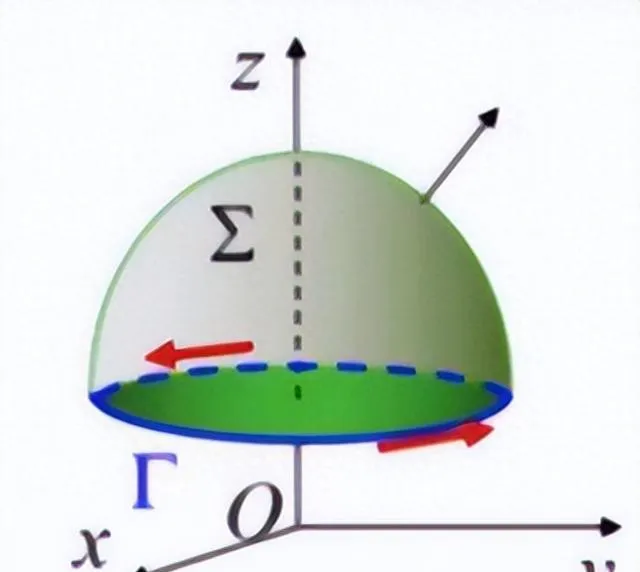
斯托克斯公式:设Γ是分段光滑的有向闭曲线,Σ是以Γ为边界的分片光滑的有向曲面。Σ的侧与Γ的正向符合右手规则,P,Q,R在包含Σ在内的一个空间区域内具有连续一阶偏导数,如上图。则有:
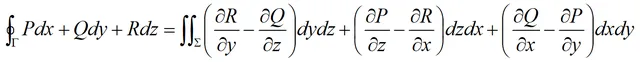
此式称为斯托克斯公式。
下面给出斯托克斯公式的推导过程:
由于P,Q,R是不相关的,这里只证明与函数P相关的信息,其余的可类似证明。
(1)设曲面Σ与平行z轴的直线相交不多于一点,方向取为上侧,如上图。其方程为:
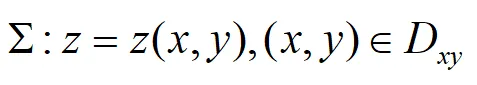
根据两类曲面积分的关系可得:
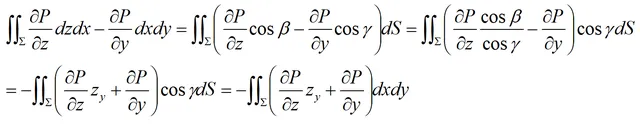
其中:
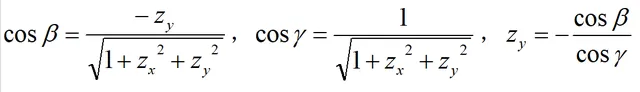
根据一代二投三定向的步骤及多元函数链式法则:

再将曲线Γ投影到xoy面为L,如下图:
根据格林公式可得:

如果Σ取下侧,曲线Γ也相应地改成相反方向,上式的两端同时改变符号,因此上式仍然成立。
(2)进一步地,若曲面Σ与平行于z轴的直线的交点多于一个,则可以添加一些辅助曲线分成几部分,然后利用前面的公式计算并相加。因为沿辅助曲线而方向相反的两个曲线积分相加时正好抵消,公式仍然成立。
同理可证其它两项表示式,因此证得斯托克斯公式成立。
为便于记忆,斯托克斯公式还可记作:
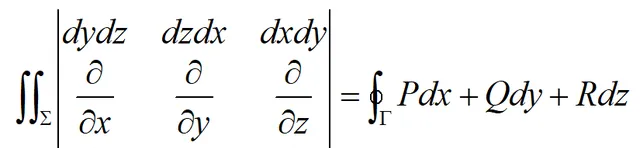
或用第一类曲面积分表示:
特别地,若Σ是xoy面上的一块平面区域,则斯托克斯公式就是格林公式,故格林公式是它的一个特例。
下面通过一个例子加深理解。求对坐标的曲线积分
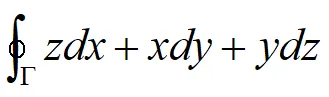
其中曲线Γ为平面x+y+z=1被三坐标面所截三角形的整个边界,方向如图所示。
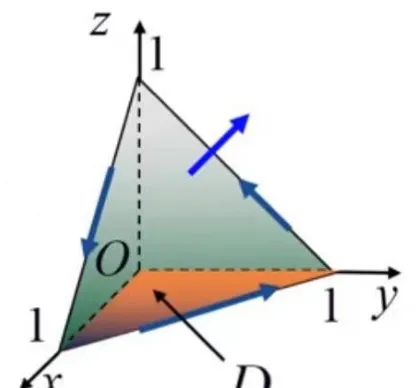
解:记三角形域为Σ,方向取上侧。根据斯托克斯公式可得:
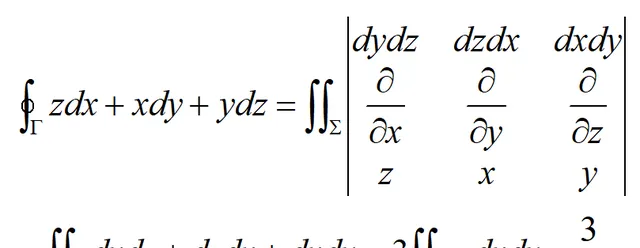
希望本文对你学习斯托克斯公式有所帮助。











