上一篇给出了常数e和π是无理数的证明,前面说了 超越数的证明比无理数的证明要困难地多 ,100年后,1873年法国数学家埃尔米特证明了e是超越数,其过程中的一个定理后来发展成著名的 林德曼-魏尔斯特拉斯 定理,这个定理的强大之处在于可以证明一系列数是超越数,从而让e和π的超越性可由该定理直接导出。回忆前面证明e是无理数的方法,是根据一个e的无穷级数,利用反证法假设e是有理数,即可建立关于有理数的方程,而有理数经通分就是整数,所以最终是 通过关于整数的方程推出矛盾 。证明超越性的困难在于,假设e是代数数,它是某一多项式的根,无法像有理数一样把它写成两个整数之比。

我记得有数学家说过, 要是缺点灵感,就去读读19世纪的数学 。我觉得学习数学,不能抛开数学的发展史。在西方, 数学专业拿的是文学学士 ,这也佐证了我的一个观点。 相比数学和科学的距离,我认为数学离文学更近 。数学中所研究的对象并不是自然界存在的对象,而是人的意识所创造的。所以很多科普博主是把数学和物理、化学甚至工科中的人工智能融在一起,而 我更倾向于将数学和文学、心理学相融合 ,这也意味着我所介绍的数学是纯粹数学而不会是应用数学。 数学研究有其逻辑的成分也有其直觉的部分 。从心理学荣格八维的角度看,有的人是直觉主导、有的人是逻辑主导,他们所呈现的数学也是不同的。我个人是直觉先于逻辑,所以更倾向于一针见血直指本质的内容。下面介绍如何证明e是超越数,所用的证明方法比较初等,只需会一点微积分就可以理解。
证明 :反证法,假设e为某个n次整系数多项式g(x)的根,
接下来一步很关键,对于任意的多项式p(x),假设最高次为r,构造多项式P(x),

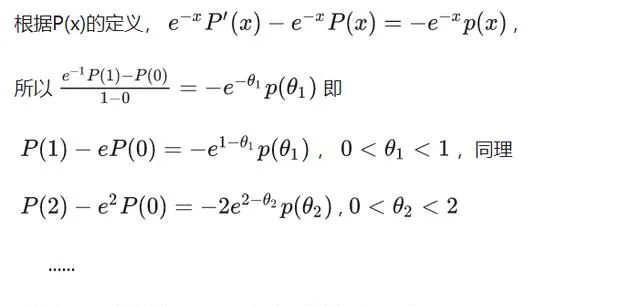

到这儿,我们的证明已经完成百分之八十了,后面只是一个技术性的验证。很多时候我们看别人的证明能看懂,但是自己却不能找到证明的方向,这是为什么? 那就是没有思考别人为什么要这样做 ?数学家为何要构造P(x)这样的多项式?注意 上式是个恒等式,也就是不论e是不是超越数上式都成立 。只不过当e是超越数时,其中的式子

只要e是超越数,这个式子必然能推出矛盾 。现在的问题是通过什么方式推出矛盾。回忆证明e是无理数的过程,通过等式两边一个是整数一个是小数推出矛盾。有的读者会思考,存不存在两边是不同整数的情况,使我们推不出矛盾。这种情况不存在,因为 若e是超越数,将它代入到整系数多项式里一定是小数 ,若是整数,那我们让这个多项式减去该整数,还是个整系数多项式,那么e就不是超越数了。
这个多项式的特点是1,2,...,n处是q重根,在0处是q-1重根,可以推出(1)式左边是个 非0整数 。最后的工作就是推出右边是个小于1的数了,比较简单留给读者思考。

在e是超越数被证明之后,林德曼很快证明了π是超越数,沿用了埃尔米特的方法, e和iπ通过一个很经典的公式欧拉公式联系起来 ,林德曼证明了iπ是超越数,那么π必然是超越数了。
再过了几年,一个更一般的结论出现了,由它可以导出一系列数是超越数,它就是 林德曼-魏尔斯特拉斯定理 。

随着π是超越数被证明,困扰人类几千年的数学问题 化圆为方 问题被彻底解决。











