第三章 一次函数
在第二章里,我们曾经看到过象
W =7.8V, y =0.6x,
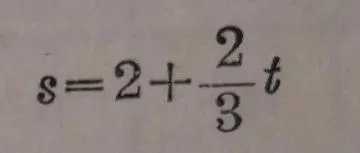
之类的函数.这些函数的共同特点是等号右边的式子都是自变量的一次式。通常我们把具有这种特点的函数叫做关于这个自变量的 一次函数 。它是函数中最简单的一类。这一章里,我们将研究这类函数。
§3.1函数 y = kx ( k ≠0)
1.正比例关系 我们来考察§2.1里举过的铁的重量 W 和它的体积V之间的函数关系:
W =7.8V,
这里7.8是每立方厘米的铁块重量的克数.
如果令铁的体积分别是1立方厘米,2立方厘米,3立方厘米,……就可以算出和它对应的重量如下表:
表格

这里我们看到:当体积 V 扩大(或者缩小)若干倍的时候,重量 W 也随着扩大(或者缩小)相同的倍数.在算术里,我们已经知道具有这样性质的两个量,叫做 成正比例关系的量 .
从这个表里,我们还可以看到: W 的任何一个数值和它所对应的 V 的数值的比,是一个常数.例如
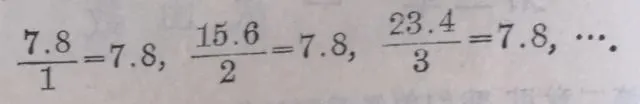
一般地,我们有

这里常数7.8叫做变量 W 和 V 间的比例系数。
因为在算术里,我们所学过的数只有正数和零,所以当时所研究的成正比例的量的比例系数都是正数.现在,我们已学习了负数,需要把算术里学过的成正比例的量的定义加以推广。
我们来看下面的例子:
一列火车,以每小时40公里的速度,自东向西行驶,在中午到达甲站。求在中午以前½小时,1小时,3/2小时,以及中午以后½小时,1小时,3/2小时,火车离开甲站的距离.
我们把自西向东的方向作为正的方向(图3·1),那末这列火车行驶的速度可以记作
v =-40公里/小时。
图3.1
设在中午后 t 小时(在中午以前, t 用负数表示;中午以后, t 用正数表示)火车离开甲站 s 公里(在甲站以东, s 是正数;在甲站以西, s 是负数)。那末可得 s 和 t 之间的函数关系
s =-40t.
这样就得到下面的表:
表格

这里,我们也可以看到 s 的每一个值和它对应的 t 的值的比是一个常数,就是
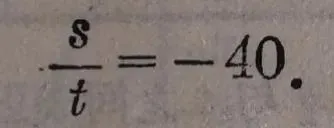
我们也把变量 s 和 t 之间的这种关系叫做正比例关系,把这个常数"-40"叫做 s 和 t 之间的比例系数.
一般地说:
两个变量 y 和x间的函数关系,如果能用公式
y = kx(这里 k 是一个不等于零的常量)
来表示,那末这两个变量间的函数关系就叫做正比例关系, k 叫做比例系数。
习题3.1(1)
1.下列各种关系里,哪些是正比例关系?为什么?
(1)正方形的周长 p 和它的一边的长 a ;
(2)正方形的面积A和它的一边的长 a ;
(3)圆的周长 C 和它的直径 d ;
(4)圆的面积 A 和它的直径 d ;
(5)速度 v 一定的时候,所走的距离 s 和所需的时间 t ;
(6)时间 t 一定的时候,运动的速度 v 和所走的距离 s;
(7)距离 s 一定的时候,运动的速度 v 和所需的时间 t ;
(8)比重 d 一定的时候,物体的重量 W 和它的体积 V ;
(9)体积 V 一定的时候,物体的重量 W 和它的比重 d ;
(10)重量 W 一定的时候,物体的体积 V 和它的比重 d .
2.把上面这些关系中,成正比例关系的写成 y = f ( x )的形式,并求出每一个关系中的比例系数.
3.把汽油用均匀的速度注入桶里。注入的时间和注入的油量如下表:
表格
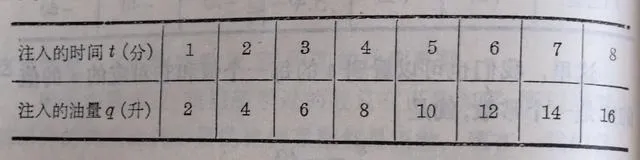
(1)从表里的数据,证明 q 与 t 之间成正比例关系;
(2)求比例系数(q/t);
(3)用解析法表示出 q与 t (把 t 作为自变量)之间的函数关系;
(4)求 t =1.5, 4.5时 q 的对应值.
2.函数 y = kx 的图象 我们先来作下面这两个函数的图象:
(1) y =2x, (2)y=-2x
用§2.7里讲过的方法,我们先选择一些x的值,列成下表:
表格
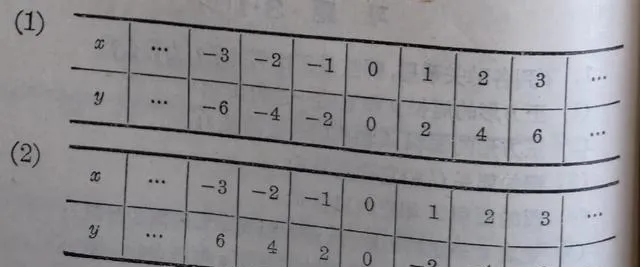
把表里的每一组 x , y 的对应值作为点的坐标,在直角坐标系里作出这些点,并且用平滑的线连接起来,就得到图3.2和图3.3.
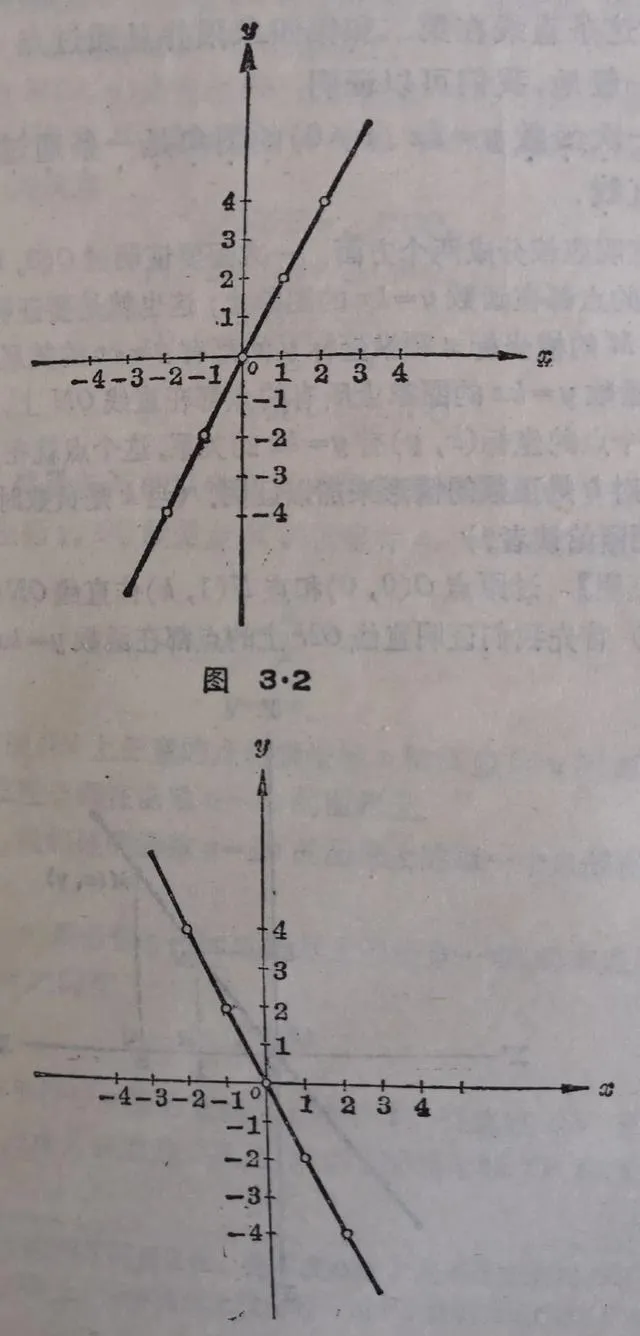
从图里可以看到这两个函数的图象都是通过原点的直线.在(1)中这条直线在第一第三象限并且通过点(1,2) ;在(2)中这条直线在第二和第四象限并且通过点(1,-2).
一般地,我们可以证明:
一次函数y= kk (x≠0)的图象是一条通过原点和和点(1,k)的直线.
*证明应该分成两个方面.一方面要证明过O(0,0)和 N (1,k)的直线上的点都在函数y= kx 的图象上;这也就是要证明,直线 ON上的每一点 M 的横坐标x和纵坐标 y 间都有y= kx的关系。
另一方面还要证明,函数y=kx 的图象上所有的点都在直线 ON 上,这就是要证明,如果一个点的坐标(x ,y)有y=kx的关系,这个点就在直线 ON 上.下面我们对k是正数的情形来加以证明.(当 k 是负数时,可以同样地证明,证明留给读者.)
【证明】过原点O(0,0)和点 N (1,k)作直线ON(图3.4).
(1)首先我们证明直线ON上的点都在函数y= kx 的图象上.
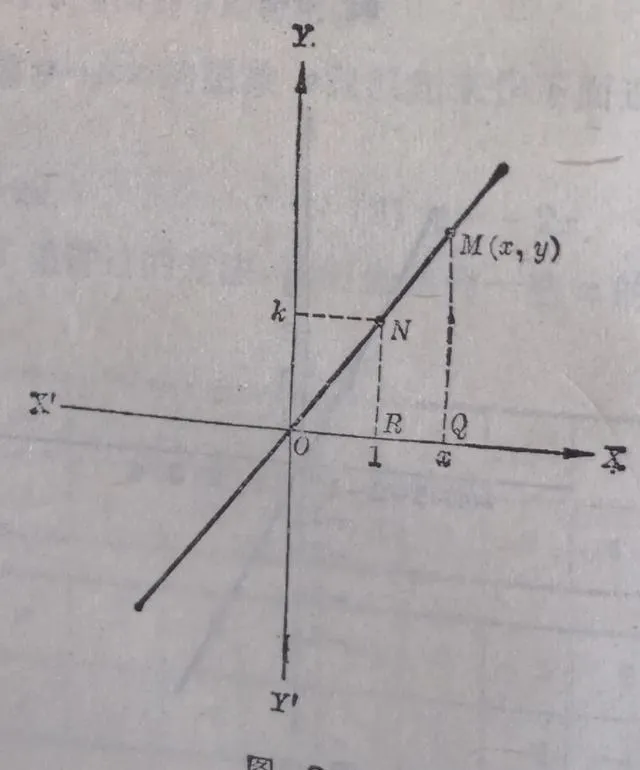
图3.4
因为原点 O( 0 ,0)的横坐标 x 和纵坐标 y 之间有
0= k·0
的关系。所以原点 O 在函数 y =kx 的图象上。同样地,因为k=k·1,所以点 N (1, k )也在函数 y=kx的图象上。
现在设点 M ( x , y )是直线 ON 上的任意一点。过点 N 和 M 分别作 y 轴的平行线 NR 和 MQ 交 x 轴于 R 和 Q .因为在直角三角形 ONR 和 OMQ 中,有一对锐角
∠NOR =<∠MOQ ,
∴△ONR ∽△OMQ .
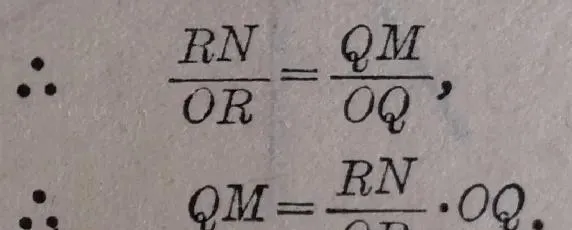
这里 RN 就是点 N 的纵坐标 k , OR 就是点 N 的横坐标1; QM 就是点 M 的纵坐标 y , OQ 就是点 M 的横坐标 x 。代入上面这个等式,就得到
就是
y = kx .
这就证明了直线 ON 上任意的点的横坐标 x 和纵坐标 y 间都有 y = kx 的关系,因此这些点都在函数 y = kx 的图象上。
(2)其次,我们证明函数y=kx 的图象上的每一个点都在直线 ON上.
设点 P ( x , y )是函数 y = kx 的图象上的任意一点,那末点 P 的纵坐标 y 和横坐标x 之间有
y = kx
的关系.
过点 P 作平行于 y 轴的直线交 x 轴于 T ,交直线 ON 于 V ①(图3.5)。那末因为点 V 在直线ON上,所以它的纵坐标 TV和横坐标OT间有
①这里我们应用了间接证法。先不考虑点 P 是不是在直线 ON 上,故意把它不画在直线 ON 上,而在直线上找出另一点 V ,然后再证明点 P 和点 V ー定重合。
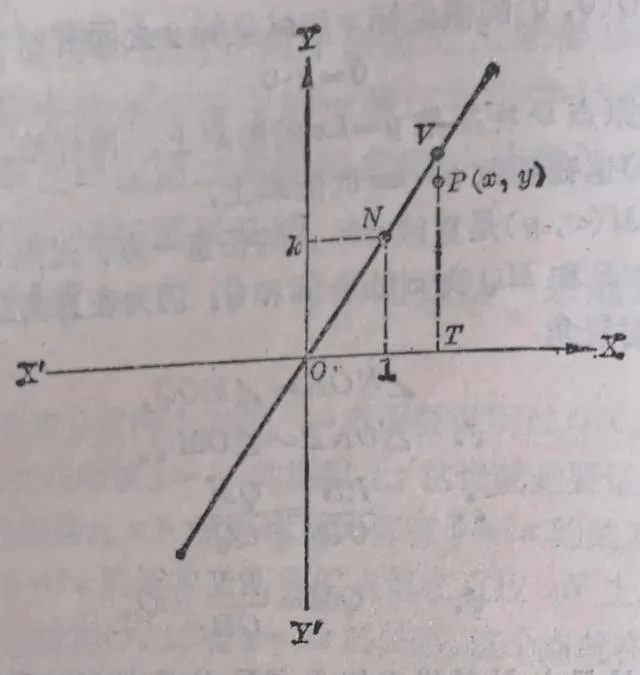
图3.5
TV=k·OT
的关系.
但是,我们已经知道,点 P 的纵坐标 y(就是TP)和横坐标x(就是OT)之间有
y = kx ,
就是
TP= k·OT
的关系。因此
TP=TV .
所以,点 P 一定和点 V 重合,也就是说,点 P 在直线 ON 上。这就证明了函数y=kx的图象上的任意一个点都在直线 ON 上。
函数y=kx的图象,以后简称为直线 y=kx .
例1.作函数 y=½x 的图象。
【解】列表:
表格

作图:
图3.6
注 要画出一条直线,只要找到直线上的任意两点就可以了。为了使画出的图精确些,我们所取的两个点要使它离开得远一些,所以这里我们取(4,2)这个点,而不是取1,½)这个点.
习题3.1(2)
1.用描点法作出习题3.1(1)里第3题函数 q = f ( t )的图象。
2.在同一坐标系里作函数
(1) y = ½x ; (2) y = x ;
(3) y =2x; (4) y =-½x
(5) y =- x ; (6) y =-2x
的图象。
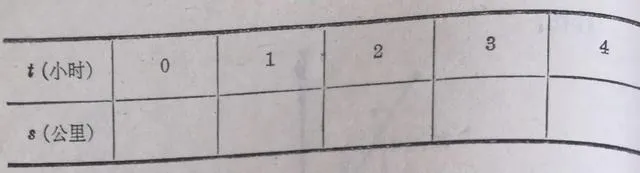
3.一个物体以每小时3公里的速度作匀速运动,
(1)把这个物体在 t 小时内所经过的路程s公里用公式表示出来;
(2)填写下面的表:
表格
(3)根据表里的数值,画出这个物体运动的路程和时间的关系的图象;
(4)根据图象找出 t =1½, t =3½时 s 的值;
(5)根据图象找出 s =27, s=10时 t 的值。
*4.证明,当 k <0的时候,函数 y=kx 的图象是经过原点,并且在第二和四象限的一条直线。
3.函数 y = kx 的性质
观察图3.2和图3.3,容易发现函数 y = kx 有下面的重要性质:
(1)如果k >0,那末当自变量 x 逐渐增大时,函数 y 的值也随着逐渐增大;这时我们说函数 y=kx 是 上升 的;
(2)如果 k<0,那末当自变量x逐渐增大时,函数的值则随着逐渐减小,这时我们说函数y= kx是 下降 的.
4.直线 y = kx 的斜率和倾角
现在我们来研究当比例系数 k 变化的时候,直线 y = kx 的位置怎样变化.
例2.在同一个直角坐标系里,作下面三个函数:
(1) y =½
(2) y = x ;
(3) y=2x
的图象.
【解】在习题3.1(2)里,我们曾经作出这些函数的图象(图3.7).
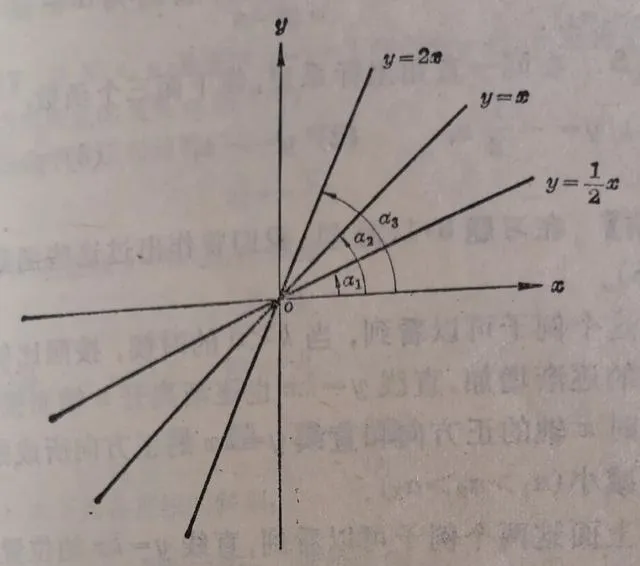
从这个例子可以看到,当 k >0的时候,按照比例系数的逐渐增加,直线就逐渐离开x轴而接近 y 轴.这时直线y=kx的正方向①和 x 轴的正方向所成的角α在逐渐增大(α₁<α₂<α₃).
例3.在同一直角坐标系里,作下面三个函数。
(1) y =-½x;
(2) y=-x ;
(3)y=-2x
的图象.
【解】在习题3.1(2)里,我们曾作出过这些函数的图象(图3.8).
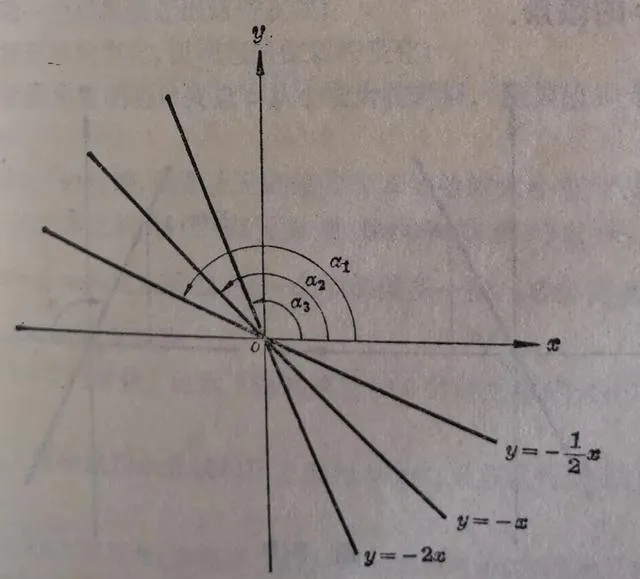
从这个例子可以看到,当k<0的时候,按照比例系数的绝对值的逐渐增加,直线y=kx也逐渐离开 x 轴而接近 y 轴。但是这时x轴的正方向和直线y=kx 的正方向所成的角α却在逐渐减小(α₁>α₂>α₃) .
从上面这两个例子可以看到,直线 y = kx的位置,和它的比例系数 k 有关。我们把 k 叫做直线 y = kx 的 斜率 ,并且把x轴的正方向和直线 y = kx的正方向所成的角α ,叫做直线 y =kx的 倾角 。
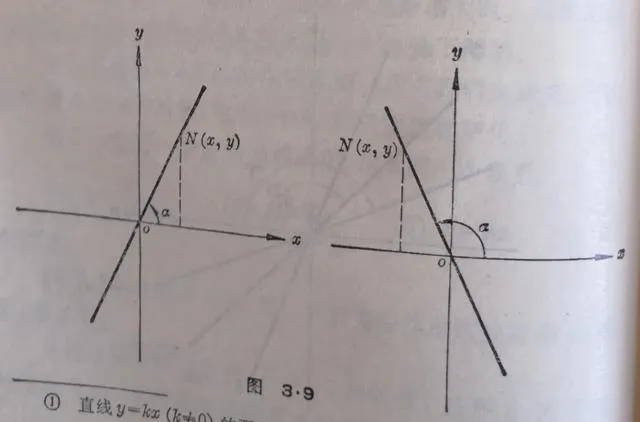
图3.9
①直线 y=kx( k≠0)的正方向指的是向上的方向。
*利用三角学中的知识,我们可以证明
k = tan α .
【证明】设 N ( x , y )是直线 y = kx 上的任意一点, x轴的正方向和直线向上方向所成的角是α(图3.9).
根据三角学中正切函数的定义,得到
tan α =y/x (1)
但是, N 在直线 y = kx 上,所以有
y/x=k. (2)
从(1)和(2)得
tan α = k .
习题3.1(3)
1.(1)求下列各直线的斜率
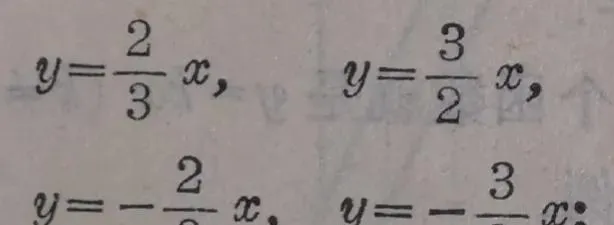
(2)在同一坐标系里作出这些直线;
(3)根据斜率的变化,说明直线位置的变化;
(4)根据图象说明当自变量 x 从小增大的时候,函数值的变化情况;
(5)当 k >0的时候,函数上升的速度和 k 的值的大小有什么关系?
[提示:从图象上研究,当自变量增加同一数值的时候,函数
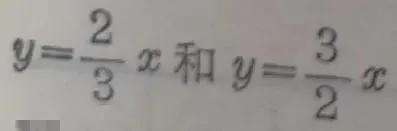
所对应的值,哪一个增加得多一些。增加得多的,就说这个函数上升的速度较快.]
(6)当k< 0 的时候,函数下降的速度和 k 的绝对值的大小有什么关系?
*2.求上题中这四条直线的正方向与x轴的正方向所成的角(精确到1°)①
①如果没有学过三角,本题可以暂时不做;如果只学过锐角的三角函数,那么可以只做k>0的时候的两个小题。
上期链接:https://m.toutiao.com/is/iNygsUFT/ - 名师彻底讲透初等函数(7)函数图象的绘制 - 今日头条
下期预告:§3.2 函数y=kx+b(k≠0)
科学尚未普及,媒体还需努力。感谢阅读,再见。











