数学思维的妙处（17）：「我命由我不由天」的数学原理

文/老余

只要持续不断的观察所有事件，直到天荒地老，则世界上所有事物都会以固定的比例发生，如果发生了让人意外的事件，人们会把这起事件认定为既定的宿命。

——雅各布·伯努利

数学，是很多人的噩梦。

按道理，我们上学的目的之一是要培养对知识的兴趣，但结果好像恰恰相反，学前班的孩子对知识各种好奇，有十万个为什么，而高考完的那一刻满地都是被撕毁的书籍，被特别照顾的就是数学书。

但这并不是你的错，也不是数学的错，而是数学老师或者说是应试的问题。我们作为理性人，不能因为别人的错而放弃学习、运用数学。

因为无论你喜不喜欢它，这个世界的底层运行逻辑，就是数学。

这是规律，不以任何人的意志为转移。

本文【数学思维的妙处】这个系列的第17篇，我们来讨论下「大数定律」，这个定律对我的影响很大，希望对你也有用处。

一、什么是大数定律？

这是概率论中的一个基本定理，说的是：当一个实验随着重复的次数越来越多，实验结果的频率（或者叫次数）会趋向于某个常数值，这个常数值就是事件发生的概率。

不够通俗，举个例子：

比如抛硬币，我们知道每次落定后正反面朝上的概率是各50%，如果只抛10次，基本不会出现正反面各5次朝上的情况（理论上的各50%）。

虽然每次哪一面朝上是随机的、是偶然的、是不可预测的、是我们无法控制的，但随着实验的次数越来越多，最终统计的结果是正、反面朝上的次数（频率）就会越趋（收敛）近于各50%。

——短期看是随机的，长期看是确定的，这就是大数定理。

1713年，雅各布·伯努利（就是那个著名的伯努利实验的伯努利）在数学上证明了「大数定理」，当我看到这个年份，其实有些意外，人类对很多数学概念启蒙的很早，比如毕达哥拉斯定理，但唯独在概率或者说在随机这件事上，是很晚熟的，可见人类是多么不习惯随机。

就这么一个定理，能给我们什么启发？

其实很深刻。

我们接着聊。

（二）大数定理与命运

我们总感叹人生无常或者命运注定，人的命运真是注定的吗？

看上去确实如此，不然为何那么多文艺作品总是把「改天换命」作为主题呢，「我命由我不由天」这句台词，不也引起了无数人的共鸣嘛。

这起码说明了两件事：

改命难吗？

难！

没有数学之前，我们连命运的定义都无法统一，你看几千年来，用文学语言来解释、阐述命运而写成的书、编成的戏何止车载斗量。

我们从这些海量作品中学到的，也不过是四点：遇贵人、站对队、坚持住和运气好，但这些都是因人因时因地而异，不具有普遍性。所以你看时头头是道，做时一脑懵逼。

但用数学的语言来描述，命运其实很简单，其实就四个字——大数定律。

怎么说？

伯努利证明大数定律是伟大的，有意思的是他在证明的手稿边上写了一段话：

只要持续不断的观察所有事件，直到天荒地老，则世界上所有事物都会以固定的比例发生，如果发生了让人意外的事件，人们会把这起事件认定为既定的宿命。

所以，命是什么？是我们人生中的一次次选择，就像那一次次抛在空中的硬币，运是什么？是我们一次次选择后拼成的结果。

命运，就是我们一辈子所有选择的集合。大数定理，是命运的数学原理。

知道了这些又有什么用呢？

有大用！

因为，我们借此可以主宰自己的命运，可以「我命由我不由天」了。

（三）大数定理，如何指导现实生活？

我看到了两点：

1、大数定理，能减少了我们的精神内耗

这个时代选择很多，这是好事，选择更多意味着我们可以「树挪死，人挪活」，可以此处不留爷自有留爷处。

但选择多也是坏事，这会让我们频繁挪、频繁去别处。而一个人的时间和精力是有限的，频繁的挪，你怎么可能和原本就在这个行业浸淫的小伙伴竞争？

这正印证我小时候的印象较深的这幅挖水的漫画。

我们很多时候之所以打几枪换一个地方，到处去找所谓的风口，大概率是因为不了解「大数定理」：

——在一个行业里深耕，我们才有机会在这个行业里「抛硬币」，只有一次次去抛，只要抛的次数足够多，频率就会收敛于概率，你期盼的结果才大概率会出现。

这是定律，与你是否高明动作是否优雅无关。

你看，绝大多数人为何一辈子碌碌无为？

或许不是因为不够聪慧，而是过于聪慧，刚上这张桌抛了几次没有得到想要的，就已经在去找别的桌子的路上了。

他自己的理解可能不是努力的时长不够，而是之前选的方向错了，于是成了那个挖井水的人，到处挖，忙得不可开交，过年连家人都没时间陪，但我们知道，他就是漫画里挖水的那个人，注定得不到想要的结果。

这是第一点，既然已经选了这个行业，且这个行业没有被淘汰，那就坚定信心往前走，随着「抛硬币」的次数越来越多，频次必然越来越接近于固有概率。

即使这个行业整体沉没了，我们的选择也要与之前的沉淀有相关性，千万别相信什么「心若在梦就在，只不过是从头再来！」

那是歌词，不是现实，你让刘欢从头来一次试试？凡是歌里提倡的，都是有坑的，都是希望你来填的，别犯傻。

2、大数定理告诉我，何事惊慌？

我们来做个游戏：

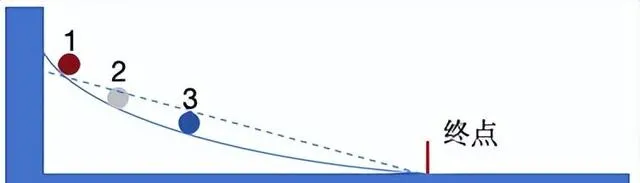
下面斜坡上高低不同的位置有三个球，分别滚下，滚到右侧平面的终点用时最短即获胜，你觉得哪个球会赢得比赛？

表面上看，3号蓝色因为离终点最近，所以直觉上3号应该赢得比赛，但实际情况是，只要这个斜坡是「等时曲线」，1、2、3号到达终点的时间是一样的。

注：在「等时曲线」上，不同位置的球到达终点的时间一样，由荷兰数学家惠更新在1673年发现。

等时曲线还有一个特性，就是球从这条曲线的这个点滚下去，比其他任何曲线和直线滚下去的时间，都最短的。

比如1号球，从同等高度的等时曲线（实线）往下滚，就比从直线（虚线）上滚到终点用时少。

那这个时间是多少呢？

直接给答案，t=π ，你看，「π和g」（g是重力加速度）都是常数，所以时间只与「r」有关。

这意味着，只要这个球在这条赛道的「等时曲线」上，无论它从哪个位置、什么高度出发，他到达终点的用时是最短的。

这和我们的职场赛道是一样一样的，当我们进入一个行业，重要的不是埋头去努力去堆积一万小时定律，而是要先抬头去找那条「等时曲线」，通俗地说，就是不要用战术的勤奋掩盖战略上的懒度，先找到实现目标的最短路径。

耐心找到这条曲线，不要着急，过程中遇事不要惊慌，因为你知道，要是运气好，你期待的结果会来得比较早，即使运气不咋地，你也很笃定结果最终会到来。

既然事情的发展有自己的内在规律，那我们就把自己能掌控的事做好，把不能掌控的事交给规律，交给大数定律。「急、慌」等情绪不仅对于事情的发展没有帮助，还有可能适得其反，慌乱之中乱动作，走错步出错棋。

埃隆马斯克送到太空中的那辆特斯拉跑车，驾驶室屏幕上就写着「Don’t Panic（不要惊慌）」。

（四）结语

天地不仁以万物为刍狗。你有你的情绪，但世界的运行是冷酷的，是由各种冰冷的定律组成的。

人类社会，就是一个大型的伯努利试验场，对于冷面的命运之神，每个个体就是她手里的那一枚枚硬币，少部分人会受到命运之神的青睐，他们一出生就在罗马，但绝大部分人，一出生注定就是骡马。

但万幸，现在留给我们这些绝大多数人的，还有「选择」与「时间」。

但只要有这两样，我们就能去探寻人生的概率，人生无常，但我们仍能从中发现一些「有常不变」的东西，英国作家白哲特说：「生活是概率的学校，在这所学校里，我们每个人不应该甘心当一个被扔来扔去的骰子。」

2023年，楼市有巨大的上涨空间，股市给我们埋下了巨大的上涨希望，职场也是灵活就业的人越来越多，很多人说24年也不要抱有太大期望，我不敢说太多。

在【乐队的夏天】的第一季里，九连真人的一首歌让我印象深刻——【莫欺少年穷】，为何莫欺少年穷？

因为少年们最大的优势，就是拥有从「频次收敛到概率」过程所具备的核心因素：

——时间。

（完）