微分到底是什么?在我们初学微积分的时候必然会遇到这个问题,人的大脑具有一种能力,即在看到某些文字时能够联想到相应的形象。例如,当看到「小狗」这两个字时,闭上眼睛我们就能想到只属于自己的小狗的形象。此时此刻,当听到微分这个词时,你可能还想不起来任何具体的形象。
没关系,我们可以跟着【蚂蚁微积分】这本书的主角,借助小小的蚂蚁,将微积分的核心概念和原理用最简单、最有趣、最容易理解的方式呈现出来。轻松入门微积分。

来源 | 【蚂蚁微积分:超简单超有趣的微积分入门】
作者 |[韩]张志雄
译者 | 李光哲
求蚂蚁所感知的山的倾斜度
小学学过的九九乘法口诀是一种基础的数学工具,能够快速计算出同一个数的连加。微分概念和九九乘法口诀一样,也是一种数学工具。那么,微分究竟是什么呢?
解释微分概念的方法有很多种。为了便于理解,我们需要做几个想象实验。在这些想象实验中,将会出现虚拟的蚂蚁。我们就把这只虚拟的蚂蚁叫作「微分蚂蚁」吧!在故事中加入微分蚂蚁,是为了从视觉上简单易懂地表示「点」这一几何学概念。
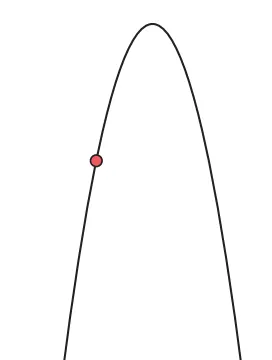
想象一下,在上面的图像中找一个点,并对这个点及其附近的区域进行放大,如下图所示。
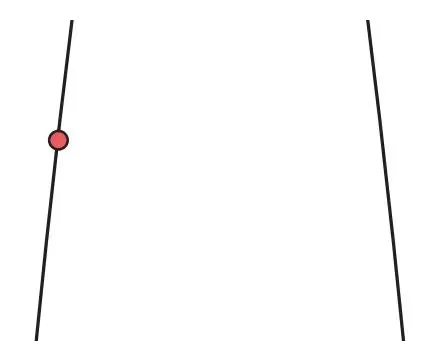
在我们所要研究的点上,总会有微分蚂蚁陪伴我们。接下来要出场的微分蚂蚁的形状如下,它的大小相当于一个点,它能够在各种图像上自由移动,帮助我们研究微分。
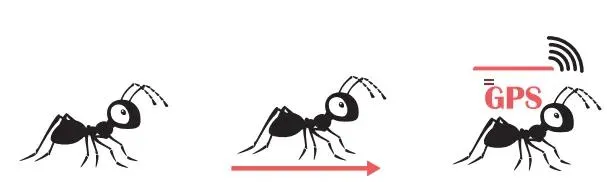
本书将出现以上 3 种微分蚂蚁,分别是普通微分蚂蚁、箭头微分蚂蚁和 GPS 微分蚂蚁,它们各有特点。本书将根据故事情节的需要选择适合的微分蚂蚁登场。故事的开始由最简单的普通微分蚂蚁拉开帷幕。
微分蚂蚁想象实验
想象一下,有一座像下图一样的山,山上有一只微分蚂蚁正在爬行。与这座山相比,这只虚拟的微分蚂蚁非常小。微分蚂蚁虽然在山上爬行,但是它并不知道山的整体形状。不过,这只微分蚂蚁具有感知山的倾斜度的能力。
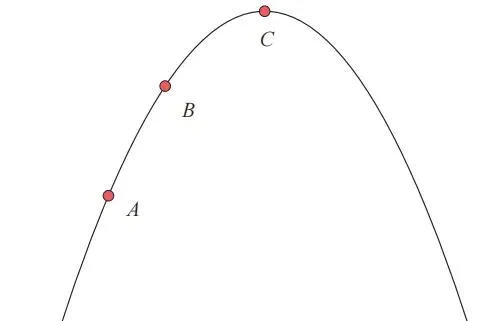
当微分蚂蚁从 A 点出发,经过 B 点,最终到达山顶 C 点时,微分蚂蚁在这 3 个位置上感知到的山的倾斜度如下图所示。
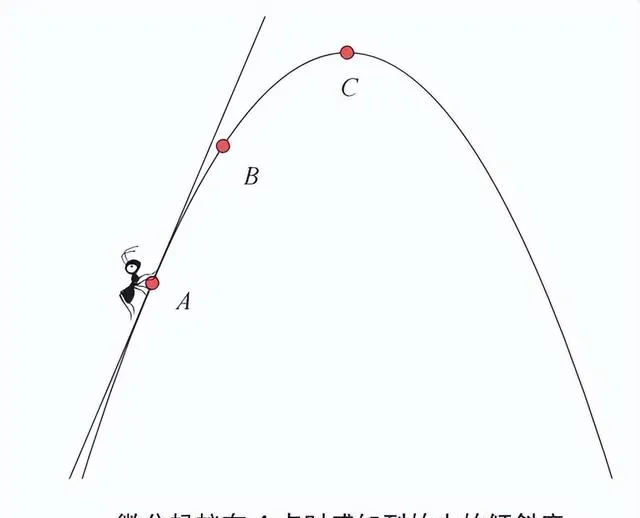

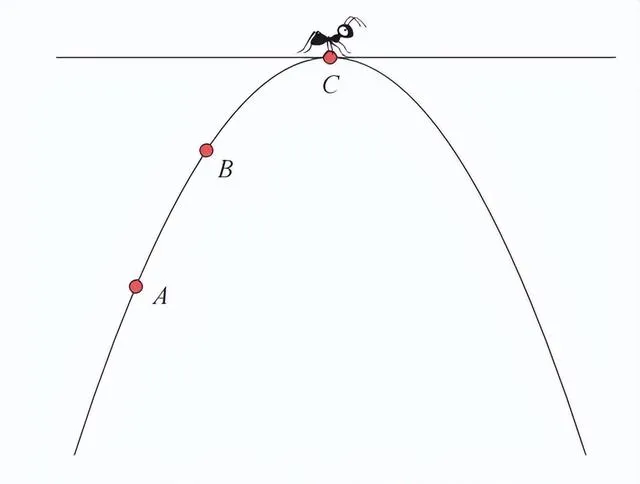
由于微分蚂蚁能够准确地感知它当前所在位置的倾斜度,因此它会觉得 A 点的倾斜度大于 B 点的倾斜度。同时,在登上 C 点的瞬间,微分蚂蚁会觉得山是平缓的。可以说,微分蚂蚁在各个位置感知到的倾斜度就是微分的概念。从严格意义上来说,与「微分」有关的部分是计算相应位置的「切线的斜率」。在与微分相关的各种图像中,上面的图像是最典型的。
如上所述,微分与曲线上某一点处的切线斜率有关。在这次想象实验中,微分蚂蚁爬行的山的形状是一条光滑的曲线。让我们进一步关注曲线上的 3 个点A、B、C 处切线的斜率。如果从微分蚂蚁的角度来看,用微分的概念来描述曲线的形状,可能的表达方式如下。
在给定曲线的点 A 和点 B 处,切线的斜率均为正数,点 A 处的切线斜率大于点 B 处的切线斜率。点 C处的切线为水平线,其斜率为 0。
这种用斜率描述曲线形状的方式,就是用微分语言描述曲线的方式。通过微分蚂蚁想象实验,我们可以直观地理解微分这一数学概念。
微分蚂蚁要爬行的山的形状
在微分故事中,有几个关键要素,其中最重要的是微分蚂蚁要爬行的山的形状。本书所研究的山大致有以下几种形状。





微分蚂蚁要翻越的山的形状,我们称之为「图形」。图形的准确形状可以利用函数的概念进行研究。微分课程的目标在于:当给定各种函数时,如何找到切线的斜率。本书将为你更直观地理解这一过程提供帮助。
画出普通微分蚂蚁感知的切线
一听到「微分」这个词,你可能会担心遇到可怕的算式和特别难的公式。然而,这种担心其实是没有必要的。有关微分的算式,最后稍加整理即可得出结果。
调动全身的感官来体会和熟悉微分才是我们讲微分蚂蚁的故事的目的。在前面,我们把微分的概念理解为,当微分蚂蚁被放在给定函数上时,它所感知的倾斜度。简而言之,微分是对切线的研究。只要完全抛开算式,亲自动手画各种切线,你就能直接感受微分的概念。
请使用铅笔在普通微分蚂蚁所在的位置处画切线。微分蚂蚁在曲线上移动时感知的倾斜度
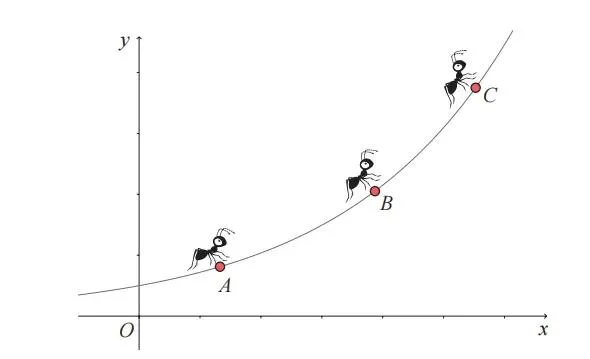
当微分蚂蚁分别位于上述图像的 3 个点上时,请使用铅笔在相应的点处画切线。
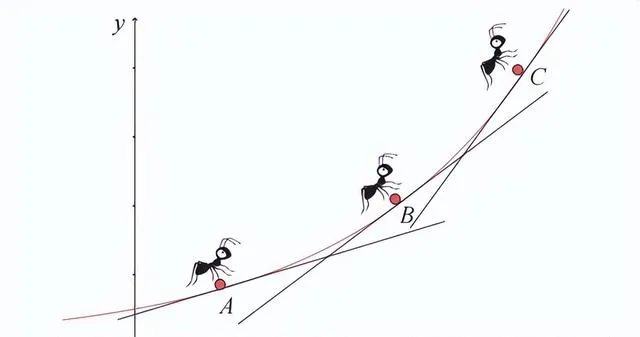
切线的大致形状如上图所示。如果给定一个图像,我们可以在大脑中想象「某一点」处的切线,并用可视化的方式将其呈现出来。这只需要一支铅笔即可完成。在上图中,我们任意选择了 3 个点并画出了切线。如果说微分是找到切线的正确方法,那么在上图中特定的 3 个点 A、B、C 处画切线,相当于对其进行微分。如下图所示,我们可以利用函数 f、函数上的点和该点处的切线来表示这种情形。
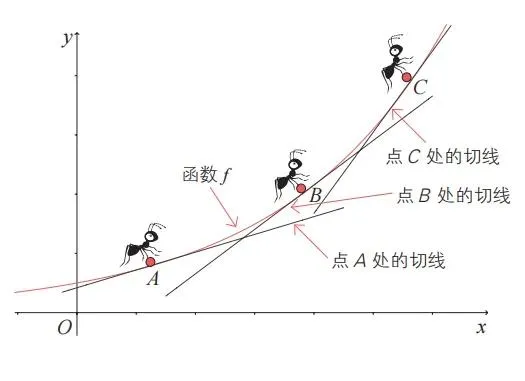
微分蚂蚁正在爬行的图像可以视为某个给定函数的图像。这意味着,微分蚂蚁位于函数上,函数是微分的研究对象。在这个函数图像上,回顾一下任意 3个点 A、B、C 处的切线。对某个函数求微分,意味着可以在任意点处找到切线。也就是说,无论微分蚂蚁位于函数图像的哪一点,都能够在该位置处找到切线。我们再思考一下这些切线的斜率(微分蚂蚁感知的倾斜度)。通过微分,我们可以知道切线的斜率。在上面的图像中,点 A 处的切线斜率小于点 B 处的切线斜率,点 C 处的切线斜率大于点 B 处的切线斜率。在从点 A 到点 B,再到点 C 的位置变化过程中,切线的斜率呈递增的趋势。
这样的说明就是利用微分语言描述函数的方式。当然,目前我们是在完全脱离公式的情况下,仅用一支铅笔直接在函数图像上画切线来求微分,因此无法求出切线的准确斜率。不过,我们可以据此推测出切线斜率的变化趋势。
微分蚂蚁在直线上移动时感知的倾斜度微分蚂蚁可以在任何函数图像上爬行。如果要对某个函数求微分,只需将微分蚂蚁放在自己想研究的位置上进行思考即可。微分蚂蚁的故事中出现的大部分函数图像是曲线。不过,也不一定非得是曲线,它有可能是一条直线。将微分蚂蚁放在直线上的情形反而更特别。我们来看下图。
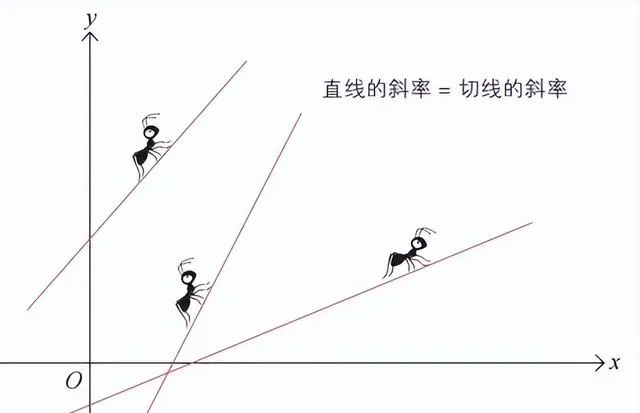
当微分蚂蚁在某条直线上爬行时,试想一下「微分」。此时,微分蚂蚁觉得直线上所有点的倾斜度(切线的斜率)都是一样的。因为直线的斜率本身就是微分蚂蚁感知的倾斜度,切线的斜率也就是直线的斜率。
在上图中,直线的斜率都是正数。有时,直线的斜率也可能为负数,如下图所示。
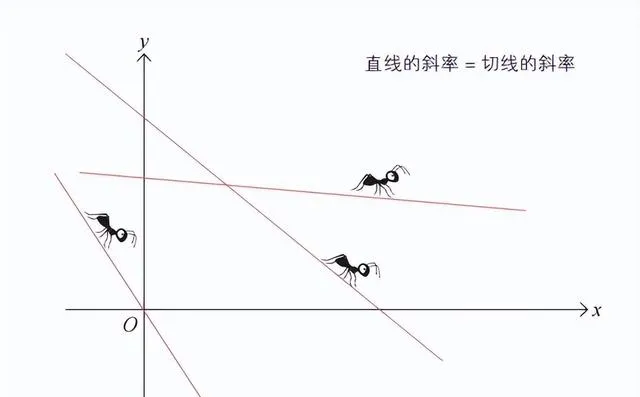
在上图中,直线的斜率均为负数。同样,微分蚂蚁所感知的倾斜度与直线的斜率完全相等。最后,让我们来思考一下微分蚂蚁在水平线上爬行的情形。请看下图。

水平线的斜率为 0。因此,当微分蚂蚁在上图的水平线上爬行时,它所感知的倾斜度为 0。也就是说,如果对水平线求微分,其结果为 0。
通过亲自动手绘制不同情形下的切线,我们对微分有了直观的感觉。只要有一支铅笔,我们就能够在给定函数的某点处画出切线,从而感知微分。
跟着 GPS 微分蚂蚁学微分
在普通微分蚂蚁身上安装全球定位系统(GPS),普通微分蚂蚁就变成了 GPS 微分蚂蚁。因此,当它在图像上移动时,可以实时接收它的坐标 (x, y)。GPS 微分蚂蚁可以利用接收到的坐标值计算斜率,并将其显示在屏幕上。
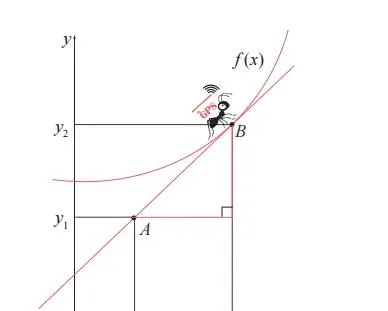
假设我们要在函数 f(x) 上求 B 点处的微分。想象有一条过点 B 的切线,GPS 微分蚂蚁正在该切线上移动。GPS 微分蚂蚁在经过点 A 和点 B 时,能够通过 GPS 准确接收点 A 的坐标 (x₁, y₁)和点 B 的坐标 (x₂, y₂)。它利用这些信息计算出了该切线的斜率,如下所示。

计算得出的斜率值会显示在 GPS 微分蚂蚁背部的屏幕上。因为我们还没有学过计算微分的具体方法,所以需要亲自动手画切线,并通过微分蚂蚁感知的倾斜度来理解微分。有关微分的所有具体计算,暂且都交给 GPS 微分蚂蚁来完成。我们的重点是借助 GPS 微分蚂蚁以多种方式了解微分的特点。
GPS 微分蚂蚁想象实验
我们可以通过二次函数 y=x² 来了解微分的概念。
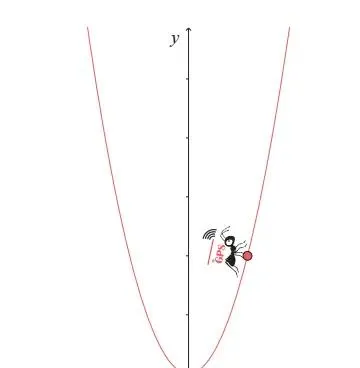
上图是二次函数 y=x² 的图像,它关于 y 轴对称,开口向上。我们将 GPS 微分蚂蚁放在图像的任意点处,然后开始做一个想象实验。
GPS 微分蚂蚁能够接收到当前所处位置的坐标,并在屏幕上显示出坐标 (2, 4)。如果要求点 (2, 4) 处的微分,目前唯一的方法是在该点处直接画切线。画出切线后,让 GPS 微分蚂蚁在切线上移动。GPS 微分蚂蚁在切线上每移动一步,都能够准确地确定自己的位置。
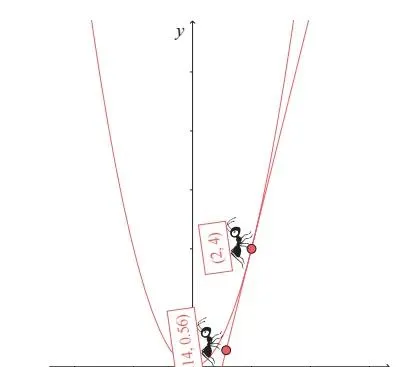
如上图所示,GPS 微分蚂蚁在切线上显示的坐标是 (1.14, 0.56)。现在,GPS 微分蚂蚁可以计算出切线的斜率。因为已经知道两个点的坐标分别是 (2, 4) 和(1.14, 0.56),所以切线的斜率是
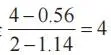
。在这里,4 既是切线的斜率,又是在点 (2, 4) 处求微分的结果。也就是说,我们可以用 4 这一特定的数值来描述 GPS微分蚂蚁在点 (2, 4) 处所感知的倾斜度。
通过 GPS 微分蚂蚁,我们终于知道了倾斜度的准确数值,不用再以「大、小」等模糊概念来描述倾斜度。由此可见,GPS 微分蚂蚁能够告诉我们具体的微分结果。请利用这一结果思考下面的问题。
当点 (2, 4) 处切线的斜率为 4 时,其关于 y 轴对称的对称点 (-2, 4) 处的切线斜率是多少呢?
回想一下图像的形状,即使没有 GPS 微分蚂蚁,我们也能立刻想到点 (2, 4) 关于 y 轴对称的对称点 (-2, 4) 处的切线斜率。答案是 -4,因为该图像关于 y 轴对称。
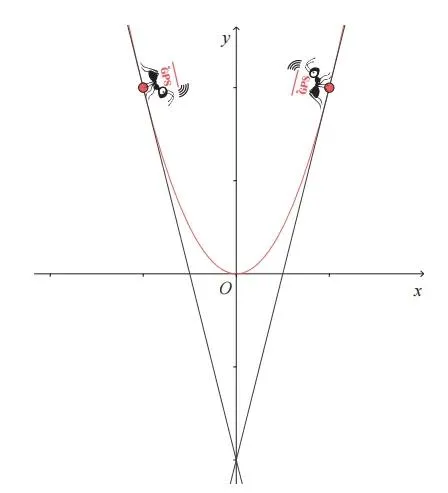
综上所述,如果在函数 y=x² 的图像上有某一点和该点关于 y 轴对称的对称点,那么我们可以同时思考这两点处的切线。只要在某一点处的切线斜率前加上负号( -),就是其关于 y 轴对称的对称点处的切线斜率。
如果我们对函数的特点和微分的概念有这种正确的理解,那么我们就能够轻松地找到切线的斜率。微分的研究对象是函数。如果在了解函数特点的基础上求微分,那么我们就能够对微分结果进行验证。
例如,在函数 y=x² 中,如果在 x >0 的区域内求微分的结果为负数,那么这个计算结果肯定是错误的。在尚未完全掌握函数特点的情况下,仅通过计算来求微分,即使出现了失误也无法进行验证。由此可见,要想正确地求微分,必须先理解给定的函数。
简单二次函数的微分
微分是指微分蚂蚁在某条曲线上的任意点处所感知的倾斜度。从 GPS 微分蚂蚁的虚拟微分工具确认的结果来看,通过计算也可以得到切线的斜率。
现在,我们来思考一下利用 GPS 微分蚂蚁对简单的多项式函数上的所有点求微分的原理。当然,所有的计算都交给 GPS 微分蚂蚁来完成,我们只聚焦于原理。
我们先对大家熟知的二次函数 y=x² 求微分。
让 GPS 微分蚂蚁从点 (0, 0) 出发,依次经过二次函数 y=x² 上的点 (1, 1)、(1.5, 2.25)、(2, 4)、(2.5, 6.25)。GPS 微分蚂蚁会计算每个点处的切线斜率,并将每个点处的切线斜率都显示在其背部的屏幕上,如下图所示。
因为具体的计算工作已经交给 GPS 微分蚂蚁来完成,所以我们只需对这一结果进行分析即可。对微分结果进行整理,结果如下表所示。
上表显示了二次函数上 5 个特定点处的切线斜率。各点处的切线斜率被称为微分系数。例如,点 (1, 1) 处的微分系数为 2,点 (2.5, 6.25) 处的微分系数为 5。需要再次强调的是,微分系数表示的是特定点处的微分结果。
由于 y=x² 的图像关于 y 轴对称,因此可以对上表进行扩展,加入关于 y 轴对称的对称点,如下表所示。
上表中增加了关于 y 轴对称的对称点处的微分系数。对于这些点,无须再次求微分,只需将相应的对称点处的微分系数乘以 -1 即可。现在,我们已经知道了 9 个点处的微分系数。在上表中,已给出的点的 x 坐标保持不变,将其微分系数作为 y 值,组成新的 (x, y),结果如下表所示。
利用上表中的点 (x, y) 画出了如下图像。
上述图像显示了原函数 y=x² 在 9 个特定点处的微分结果,即各个点处的微分系数。然而,由于二次函数 y=x² 上不是只有 9 个点,而是有无数个点,因此需要找出所有点处的微分系数。为此,我们需要使用一条光滑的直线将上述微分系数的结果连接起来。
最终,我们得到了上述图像。由此可以推测,所有微分系数的值都位于上述直线上。
综上所述,在特定点处,切线的斜率被称为微分系数,将所有点处的微分系数集合起来绘制而成的图像,其对应的函数被称为导函数。准确地说,上述图像是直线 y =2x 的图像。也就是说,如果对二次函数 y=x² 求微分,其结果为 y =2x,此时将 y =2x 称为 y=x² 的导函数。
普通微分蚂蚁和 GPS 微分蚂蚁使用不同的语言,我们运用微分语言来描述二次函数 y=x² 的图像形状。
普通微分蚂蚁认为 y=x² 的图像是山的形状,并且它能够感知每个点处的倾斜度。
普通微分蚂蚁对 y=x² 的图像形状的描述如下。
即使普通微分蚂蚁不了解微分这一数学概念,也能够做出上述这样的描述。GPS 微分蚂蚁使用更具体的语言对 y=x² 的图像形状进行描述。
综上所述,GPS 微分蚂蚁的语言能够准确地描述相应位置的微分系数,因为它使用的是微分语言。作为微分学习者,我们应该使用与 GPS 微分蚂蚁一样的描述方式。除了使用 GPS 微分蚂蚁的语言,我们还需要分析通过 GPS 微分蚂蚁获得的大量数据,做
到用一句话简洁明了地进行说明,如「 y=x² 的导函数是 y =2x」。这才是微分语言呈现出来的简洁明了的描述方式。
上文转自图灵编辑部,节选自【蚂蚁微积分:超简单超有趣的微积分入门】,【遇见数学】已获转发许可。
推荐阅读
【蚂蚁微积分:超简单超有趣的微积分入门】
作者:[韩]张志雄 译者:李光哲
本书不仅是要讲述「微分知识」,更是要与你分享「微分」的故事。我打算用故事这个最生动的方式,通过阅读本书的时候,能让你在轻松愉快的氛围中理解微积分。记得小时候,奶奶讲故事总是从「很久很久以前」开始,不管故事有多长,都能紧紧抓住我们的注意力,清清楚楚地印在我们的脑子里,最后我们还能讲给其他小伙伴听。











