
在人工智慧研究中,數學空間的術語可能會讓人望而生畏。幸運的是,要理解這些概念並不總是掌握核心AI思想的關鍵。然而,當讀者無法完全理解研究人員的意圖時,可能仍會感到不滿。本文將首先解釋一些關鍵術語,然後探討在機器學習(ML)中最相關的數學空間。數學空間的領域非常廣闊,但本文旨在在機器學習的背景下提供基礎理解,同時也為那些有興趣深入研究該主題的人提供參考。
數學空間表現出一種類似於物件導向設計的階層 。在這個階層的頂端,是最抽象的空間,如拓撲空間,它們確立了連續性和收斂性等基本概念。隨著我們在階層中向下移動,空間變得更加專門化,獲得了額外的結構和內容,以便適應特定的套用。
域(Fieds)
讓我們從討論「域」這一種數學空間開始。實數和復數都構成了域。盡管這一概念基本,但它提供了一個快速的概述,並引入了一些相關的術語。
一個域⟨F, +, ·⟩由一個集合F構成,該集合配備了兩個二元運算(即透過兩個元素產生第三個元素的運算):
實數集合ℝ構成了一個域,其中包含所有實數。對實數定義的加法(+)和乘法(·)以通常的方式進行。然而,為了符合「域」的要求,這些運算必須遵守以下公理(基本規則):
對於所有a, b, c ∈ F:
1. 在加法和乘法下封閉:a + b ∈ F, a · b ∈ F。
2. 加法和乘法的結合性:(a + b) + c = a + (b + c),(a · b) · c = a · (b · c)。
3. 加法和乘法的交換性:a + b = b + a, a · b = b · a。
4. 存在加法和乘法的單位元素:
5. 存在加法和乘法的逆元:
6. 乘法對加法的分配律:a · (b + c) = (a · b) + (a · c)
一個域在加法和乘法下是封閉的。這意味著在域內進行這些運算總會產生一個仍在同一域內的元素。
在量子力學中,復數體ℂ(由復陣列成)對於描述量子現象至關重要。有理數構成了有理數體ℚ, 而整數不構成域 。這是因為大多數整數(除1以外)沒有乘法逆元,違反了域公理中要求所有非零元素都存在乘法逆元的條件。
有序體
有序體是配備有序關系(≤)的域。有理數(ℚ)和實數(ℝ)是有序體的例子。
空間
在數學中,空間的概念雖然抽象,但卻極具力量。它始於一個集合——通常稱為點或元素的物件的集合。但僅僅是一個集合並沒有太大意義。當我們為集合添加不同的結構時,奇妙之處就發生了,這賦予了點意義和聯系。這種透過各種結構增強集合的過程催生了各種各樣的數學空間,每個空間都擁有其獨特的內容和實際套用。
空間是一個可以賦予結構的集合:
度量空間
度量空間是賦予了稱為度量的距離函式的空間,通常是理解數學空間的第一步。空間的定義通常以括弧⟨ ⟩或圓括弧 ( ) 表示,以指定集合的名稱和套用於其的特定結構。

M代表度量空間的基礎集合,它可以由數位、函式、序列或其他數學物件組成。在上下文明確的情況下,我們也可以將整個度量空間稱為 M。度量d是一個函式,它為每對元素分配一個非負實數,從而引入了它們之間「距離」的概念 。這種結構允許對距離進行分析,並且還可以討論收斂性和連續性。
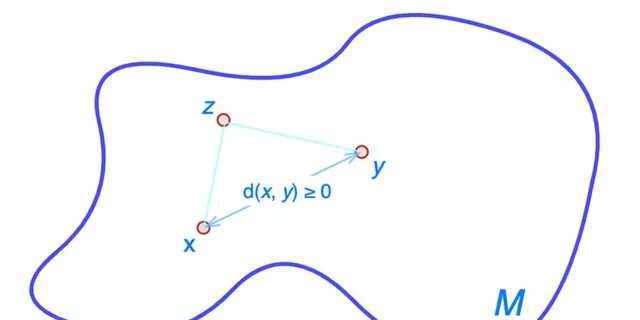
常見的度量包括曼哈頓距離(L1)和歐幾裏得(L2)距離。

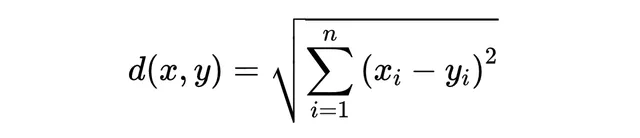
然而,度量函式必須滿足以下條件,對於所有 M 中的 x、y 和 z:
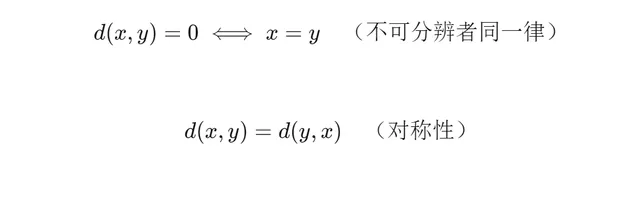
當我們設 = 時,它們得出( , )是非負的結論。
因此,這三個性質等價於以下性質。
度量的廣義定義允許廣泛的適用性和對基本概念的一致操作。例如,在生成式AI中用於更高效訓練的Wasserstein損失 滿足度量函式的標準。這使得我們可以將度量空間的性質套用於機率分布,而無需建立新的數學框架。
序列
序列為研究收斂和極限等概念提供了基礎工具。在抽象的數學空間中,將序列簡單地視為一個有序的數位列表顯得過於局限。我們需要重新建立這個概念,以適應其他數學物件(如函式),同時保留有序行程的核心思想。
讓我們在度量空間的背景下探討收斂性和極限的概念。
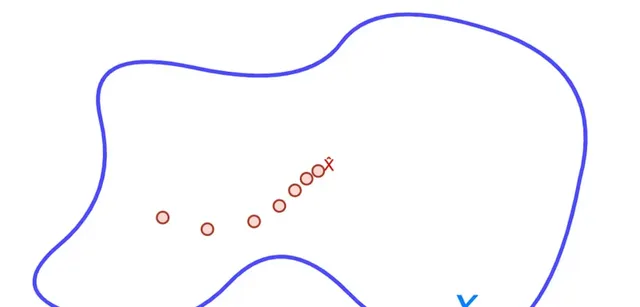
在空間 X 中的序列是指
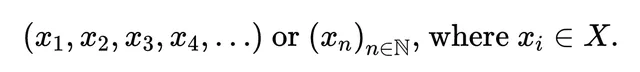
X 是一個數學空間。
度量空間中的收斂性和極限
在度量空間的背景下,如果序列的各項隨著序列的無限進行而接近一個特定的極限,那麽該序列被稱為收斂的。更正式地說,如果度量空間 中的一個序列收斂到一個極限 ∈,那麽對於每一個正數 ϵ(無論多小),都存在一個自然數 N,使得對所有 ≥,序列的項與 L 之間的距離小於 ϵ。這可以用數學形式表示為:
一個度量空間中的序列如果接近於屬於空間 X 的特定極限,那麽這個序列將有一個極限 L∈X。

然而,這種方法依賴於事先知道極限,但這並不總是可能的。為了解決這個問題,數學家們發展了柯西序列的概念。
柯西序列
柯西序列被定義為一個序列,其中的元素隨著序列的進展變得任意接近。為了使一個序列成為柯西序列,對於任意給定的正距離 ϵ,存在一個序列中的點,從該點開始,任何兩個元素之間的距離總是小於 ϵ。
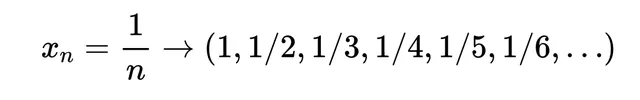
定義:對於每一個正實數 ϵ(無論多小),存在一個值 N(一個自然數,1, 2, 3, …),使得 , ≥ ,並且
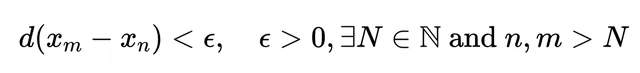
範例
讓我們考察一個在ℝ中的序列:3,3.1,3.14,3.141, …。這個序列逐次增加一位小數來逼近 π。在這個例子中,我們使用通常的度量 (,)=∣−∣。對於 <,m 項與 n 項之間的差距逐漸變小於:
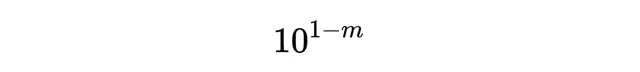
因此,對於任意正數 ε,存在一個 N,使得對於所有大於 N 的 m 和 n,m 項與 n 項之間的差距小於 ε。
完備性
一個收斂的序列總是一個柯西序列。然而,並不是所有的柯西序列都是收斂的。 舉例來說,一個完全由有理數集合 ℚ 構成的柯西序列。這個序列中的每一項都是一個有理數。
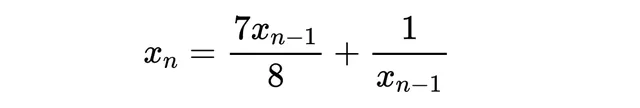
如果這個序列有一個極限 x,那麽
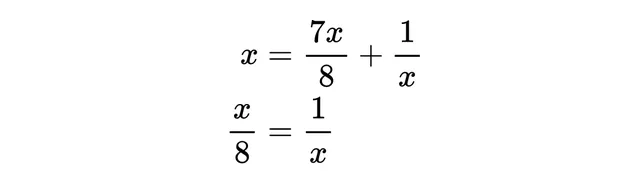
然而,沒有任何有理數可以滿足這個條件。這個序列在有理數空間中沒有極限,這意味著它並不收斂。為了使序列完備,我們可以將空間擴充套件到包含R。
如果一個空間是不完備的,那麽在這個空間中可能存在一些「缺失的點」,這些點是一些柯西序列的潛在極限點,但它們不在空間內。
如果一個度量空間中的每個柯西序列都收斂到空間內的一個極限,那麽這個度量空間被稱為完備的,確保沒有序列在收斂過程中「逃逸」出空間。
在處理不完備的度量空間時會遇到挑戰。我們可能會使用叠代方法或數值方法構造一個近似解的序列。隨著序列的進展,近似解越來越接近,形成度量空間中的柯西序列。理想情況下,我們希望這些近似解收斂到一個極限,並證明這個極限確實是一個解。然而,這種方法只有在底層度量空間是完備的情況下才有保證可行。否則,我們可能需要擴充套件這個空間。
定義域與值域
函式的定義域是指所有可能的輸入值的集合,即函式在這些輸入值上有定義。本質上,它告訴你可以輸入到函式中的內容。另一方面,函式的值域指的是函式在其定義域的每個元素上作用後所能產生的所有輸出值的集合。
連續性
極限和連續性是微分計算中的基礎構件。柯西序列提供了一種在更廣泛的度量空間背景下定義和分析極限的方法。讓我們討論度量空間之間函式的連續性概念。
如果從一個度量空間 X 到另一個度量空間 Y 的函式 f 在 X 中的一個點x_0處是連續的,那麽對於每個 ϵ>0,都存在一個 δ>0,使得對所有 X 中的 x,如果它們與x_0的距離滿足
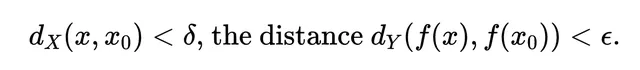
這個定義確保了在x_0附近的輸入的微小變化會導致 f(x_0) 附近的輸出產生微小變化。
在深度學習中,連續性對於確保模型輸出隨著輸入的變化而平滑變化至關重要,這有助於模型的穩定訓練。 它允許使用基於梯度的最佳化技術,例如反向傳播,這對有效訓練神經網路至關重要。連續性還有助於模型的泛化,防止預測的突然變化,從而使模型更可靠、更易解釋。
可數性
處理無限可能性是一個挑戰。在數學空間中,可數性主要旨在確保結構的可管理性和良好行為。可數性條件有助於簡化分析和拓撲學,例如存在可數基和能夠用有限集逼近元素。
一個集合如果可以與自然數(1, 2, 3, …)建立一一對應關系,則被認為是可數的。 這意味著你可以按順序列出該集合的元素。正式地說,一個集合是可數的,如果存在一個註入函式 f : F → N(自然數),使得 F 中的每個元素都可以對映到N中的一個唯一元素。
然而,這些集合可以包含無限多個元素,只要它們仍然可以順序列出,比如偶數集、整數集或有理數集。相比之下,0 到 1 之間的實數集是不可數的。 這樣的集合比自然數集要大,無法與其建立一一對應關系。
稠密性
設⟨, ⟩是一個度量空間。如果集合 ⊆ 在 中是稠密的,則對於 中的每個元素 ∈,都存在一個元素 ∈,使得 d(x, y) < ϵ 對於每個 >0 成立。非正式地說,這意味著對於 之外的任何元素,我們都可以在 中找到一個與其任意接近的元素。在 ℝ 中一個稠密子集的例子是有理數集 ℚ。為說明這一點,考慮一個實數的小數展開:
雖然序列中的每一個元素都是有理數,但序列本身收斂到一個實數。這表明,任何實數都可以被有理數任意逼近。
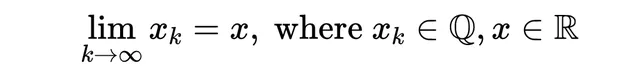
可分性
按定義,如果度量空間 X 存在一個可數集 Y ⊆ X,使得 Y 的閉包(X 中所有在 Y 中或與 Y 中點任意接近的點的集合)是 X,那麽這個度量空間稱為可分的。
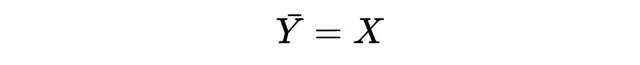
直觀上,如果一個空間是可分的,那麽 X 的每個點都可以透過可數稠密子集 Y 的點任意逼近。這意味著在 Y 上證明的性質通常可以透過這種逼近擴充套件到整個空間 X。可分性經常是某些重要定理成立的必要條件。這一性質可以簡化分析,並對整個空間產生更強的影響。
雖然將可數稠密子集直接套用於復雜的深度學習模型可能具有挑戰性,但它們的存在簡化了對各種技術的論證和分析,例如降維、核設計、逼近和數據表示。
同構
同構是指在兩個結構之間保持結構特性的一種對映,它既是單射的,又可以透過逆對映進行還原。單射對映(或一對一對映)確保不同的元素被對映到不同的元素上。
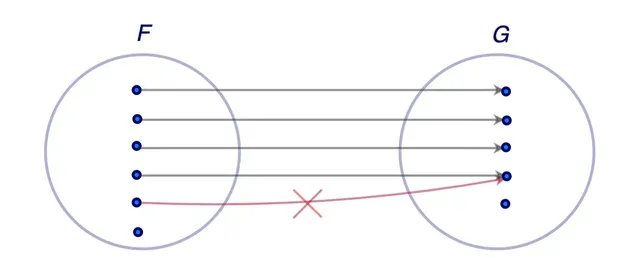
滿射對映確保目標集 G 中的每個元素至少由定義域集F中的一個元素對映到。
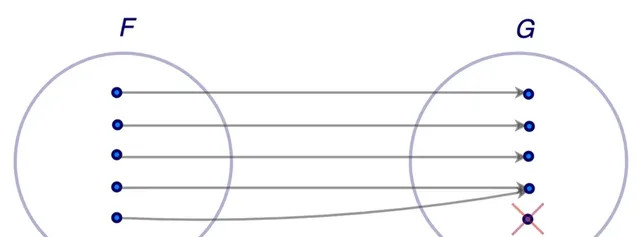
如果一個對映既是單射的(一對一的),又是滿射的(覆蓋的),那麽它被分類為對射。這意味著定義域的每個元素都對映到值域中的一個元素,並且值域中的每個元素都是由定義域中的一個元素對映來的,從而在定義域和值域的所有元素之間建立了完美的一一對應關系。
同構雖然在深度學習演算法的實作中並不直接可見,但在底層數學框架中起著至關重要的作用。它們確保了不同數學空間之間的基本結構關系的保留,這對於理解神經網路中數據變換如何影響固有資訊至關重要 。例如,神經網路中的線性變換旨在保持數據點之間的關系。同構在表示學習中尤為重要,表示學習的目標是捕捉有意義的模式,同時丟棄無關的細節。然而,像 ReLU 這樣的非線性函式雖然對於學習復雜模式至關重要,但由於其不可逆性,可能導致一些資訊的遺失。
保留性
保留性意味著運算的保留。在域的情況下,它保留了加法和純量乘法。具體來說:
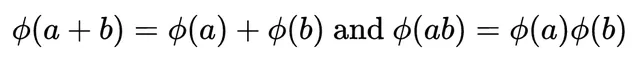
設 是從F到G 的一個對映。如果 在域的上下文中遵守所有上述規則,則該對映 是同構的。
兩個度量空間之間的等距同構(isometry)是一個保持距離的函式。具體來說,如果 (,)和 (,)是兩個度量空間,那麽函式 :→被稱為等距同構,若且唯若對於所有 ,′∈,滿足以下條件:

這意味著在X中任意兩點之間的距離與它們在Y中的像之間的距離是相同的,且依據各自的度量來衡量。
度量空間中的開集與閉集
開集和閉集是數學空間的基本構件,為發展更復雜的拓撲概念提供了必要的框架。 例如,它們在定義收斂性和連續性時是至關重要的。
開集是指不包含其邊界的集合,而閉集包含其所有的邊界點。為了便於視覺化和理解,我們將首先在更熟悉的度量空間框架內探討開集和閉集。
讓我們考察一個子集 A ⊆ X,以及一個元素 x ∈ A。

我們可以構造一個以 x為中心、半徑小於ϵ的開球B。這個球B 包含所有以下元素:
本質上,B 包括 x 及其在半徑 ϵ 內的鄰居。直觀上,這些 x 的鄰居可能都位於 A 內,或者其中一些可能超出了 A。
開集與邊界點
如果對於 A 中的每個元素 x,都存在一個足夠小的半徑 ϵ,使得以 x 為中心且半徑為 ϵ 的開球 B 的所有元素都完全包含在 A 中,那麽 A 被認為是開集。
A 的邊界點是 X 中的一個點,使得以該點為中心的每個開球都包含 A 中的元素以及 A 的補集(即 X 中不在 A 內的點)中的元素。
邊界點 x 正式定義如下:
其中 Aᶜ 是 A 的補集。A 的所有邊界點的集合記作 δA。
開集不包含其任何邊界點。
即,
閉集與閉包
閉集的定義很簡單:它的補集是開集。
i.e.
從另一個角度看,閉集包含所有的邊界點。
集合 A 的閉包是透過將 A 與其邊界點結合起來形成的。在實數集 ℝ 中,有理數集 ℚ 的閉包是整個實數集 ℝ。
如果 A 的閉包與 A 本身相同,那麽 A 就是一個閉集。
空集 ∅ 和整個集合 X 被認為既是開集又是閉集。
範例
考慮實數線上 ℝ 的開區間 = (3, 6)。
A 是一個開集。對於 A 中的任意 x,我們可以確定以 x 為中心的開球,使得這些開球中的所有元素都包含在 A 內。例如,我們可以選擇 ε 為從 x 到 A 最近的邊界點的一半距離。
讓我們探討一個更具挑戰性的範例,考慮包含在 X 中的子集 A 和 C。A 和 C 是開集還是閉集?
元素「0」和大於「3」的元素不是 A 的邊界點,因為它們本身不屬於集合 X。元素「3」也不是 A 的邊界點。以「3」為中心的任何開球都不包含既在 外又在 內的元素。
這個例子突顯了一個關鍵點:確定一個集合是開集還是閉集需要考慮集合 A 的定義以及底層空間 X 的定義,兩者共同決定了集合的邊界點 。在這種情況下,定義導致 A 的邊界點集合為空,從而得出 A 既是閉集又是開集。因此,重要的是要註意,開集和閉集並不總是互斥的類別。事實上,一個既是開集又是閉集的集合被稱為閉開集(clopen set)。
對於子集 C,元素 2 是一個邊界點。C 的閉包等於 C 本身,這表明 C 是一個閉集。
連續函式
拓撲學中的許多概念可以使用開集或閉集來定義。考慮兩個度量空間 和 以及對映函式 :→。非正式地說,如果對於 中圍繞 f(a) 的每個開球,在 中都存在一個圍繞a的對應開球,使得在f 對映下該開球的像包含在圍繞f(a)的開球內,那麽函式f在點 ∈處是連續的。
正式地說,函式 f 在點a 處是連續的,如果對於每個 ϵ>0,存在一個δ >0 使得
這意味著以a為中心、半徑為 δ的開球的像包含在以 f(a)為中心、半徑為ϵ的開球內,從而確保在 a 附近定義域的微小變化會導致 f(a)附近像的微小變化。
如果函式 f 在其整個定義域 A 上都是連續的,那麽它在 A 中的每一點上都是連續的。然而,在下面的例子中,f 在點a處不是連續的。
序列連續性
如果對於任意收斂到x~的序列(x_n),序列T(x_n)收斂到 T(x~),則函式 T 在點 x~∈X 處是序列連續的。
在度量空間中,連續性和序列連續性是等價的。
緊致性
在處理包含無限維元素(如函式或無限序列)的空間時,有限性的概念可能會變得棘手。緊致性將「閉合且有界」的集合概念從歐幾裏得空間推廣到這樣的空間。(在歐幾裏得空間中,如果一個集合包含其所有極限點,則該集合是閉集的;如果它可以包含在有限半徑的球體內,則它是有界的。)即使一個集合包含無限維元素,緊致性賦予它某種「有限性」內容。
緊致性在數學的許多領域中是一個關鍵概念,原因有幾方面。首先,它通常透過將無限情境簡化為有限情境,使得復雜問題更易處理。其次,它確保緊致集上的連續函式總是有最大值和最小值,這是極值定理中的一個關鍵思想。最後,緊致空間中的每個序列都擁有一個收斂的子序列。這一性質在分析中非常重要,因為它保證了在廣泛的情境下極限的存在。
一個拓撲空間X被稱為緊致的,如果X的每個開覆蓋都有一個有限子覆蓋。讓我們定義開覆蓋和有限子覆蓋。
有限子覆蓋是從初始開覆蓋中選出的較小的開集集合,這些開集仍然覆蓋整個集合。緊致性是一種拓撲性質,確保對於任何集合的開覆蓋,總是存在一個有限子覆蓋。換句話說,無論你如何嘗試用開集覆蓋一個緊致空間,你總是可以找到一個有限數量的開集來完成這項工作。回顧起來,問題可以透過使用有限數量的開集在局部進行分析,然後將結果匯總。
拓撲空間
拓撲空間是一種非常普遍的數學空間型別,它為定義收斂性、連續性和緊致性等概念提供了框架。它正式定義了集合內點周圍的鄰域概念,作為更高級數學理論的基礎。它建立了基本但必要的結構,這些結構本身具有有限的實際用途。通常,需要額外的結構和改進來使空間適合實際套用。
與依賴於距離函式來定義接近性的度量空間不同,拓撲空間建立在開集的概念之上。 這意味著拓撲空間不具有點與點之間的距離概念,提供的框架比度量空間更少結構性。相反,它們更關註鄰近點的概念。
拓撲空間由兩個主要組成部份構成:
開集 必須滿足以下公理:
對於給定的集合 ={1,2,3,4},X上的拓撲可以從最簡單到最復雜,取決於作為開集包含的子集的數量。任何集合上最簡單的拓撲是平凡拓撲。對於集合X,這種拓撲只包括最少量的子集:
任何集合上最復雜的拓撲是離散拓撲,其中X的每個可能的子集都被視為開集:
許多實際問題涉及的空間中只有某些型別的子集對於分析才是相關或有意義的。中間拓撲在過於簡單(平凡拓撲)和過於細粒度(離散拓撲)之間找到平衡,使它們特別適合於在理論和套用數學中進行詳細但可管理的分析。
給定一個拓撲空間 X 和 X 中的一個點 p,p 的一個鄰域是 X 的一個子集 V,它包含一個開集 U,使得
每個開集都是其每個點的一個鄰域。(註意 V 本身不需要是開集。)
在定義了鄰域之後,拓撲空間中的收斂性、連續性和緊致性的定義如下:
拓撲同構
拓撲學關註鄰域的概念。雖然度量空間包括距離的概念,但拓撲空間更加一般和抽象,因此不包含距離概念。在拓撲學中,茶杯和甜甜圈被認為是同胚的,意味著它們在拓撲上是等價的。這兩種形狀可以在不切割或粘合的情況下連續地變形為彼此。我們可以逐漸將茶杯變形,將其把手加寬,形成甜甜圈的環形。盡管這種變形改變了點之間的距離,但它保留了拓撲關註的基本鄰近關系。然而,茶杯無法變形為碗,因為這需要打孔並破壞已建立的鄰近關系。
拓撲同構,也稱為同胚,是兩個拓撲空間之間保持拓撲結構的連續函式。它是一個對射,意味著它既是一對一的(單射),又是覆蓋的(滿射),而且函式及其逆函式都是連續的。如果存在這樣的函式,這兩個空間被稱為同胚或拓撲等價。
同胚的概念在拓撲學中是基礎性的,因為它允許數學家根據空間的內在拓撲性質而非其具體幾何形狀來分類和研究空間。這種抽象有助於理解和解決數學和科學中各個領域的復雜問題。
開集基
在拓撲學中,開集對於理解拓撲空間的結構至關重要。然而,明確地定義所有開集可能是繁瑣的。基的概念提供了一個解決方案。拓撲空間的基是一個具有特殊性質的較小的開集集合:拓撲中的每個開集都可以透過基中的集合的聯集來形成。本質上,基充當了一組構建塊,可以用來構造空間中的所有其他開集。拓撲的基是一個開集集合,可以用來生成空間中的所有其他開集。
範例:實數線 ℝ 上的標準拓撲
實數線 ℝ 上的標準拓撲是由實數線上所有開區間生成的拓撲。它是由所有開區間 (a, b) 生成的基,其中 a<b 且 ,∈ℝ。這意味著這個拓撲中的任何開集都可以透過(可能是無限多個)開區間的聯集來形成。











