
扭結(繩結)理論(knot theory) 不是僅僅關於鞋帶和領結的領域,它是一個對純數學的發展和現代世界的進步至關重要的領域。有幾項發現彼此緊密相連,沒有這些發現,扭結理論是不可能存在的。繩結可以追溯到幾個世紀前,但它們在當時沒有任何數學意義。
首先,什麽是繩結? 凱爾特結 (celtic knots)是一些最早廣泛使用的繩結,遍布整個凱爾特文化。
它們是沒有起點或終點的環,歷史學家認為它們可能象征著永恒或自然界中生命的無盡迴圈。另外還有一種就是中國結,它們承載著祝福、幸福、繁榮、愛情等意義。但這些都是文化上的東西,現在讓我們進入真正的內容,即繩結的數學研究。
那麽,如何開始從數學角度研究繩結呢?在成為數學領域之前,繩結只是我們用於綁紮物品、船只、釣魚、衣物等實用的東西。我們第一次看到繩結作為數學物件出現是在亞歷山大·狄奧菲勒·範德蒙的1771年著作【位置問題的評論(Remarks on Problems of Position)】中。
範德蒙對線條或點的交織或排列感興趣。他想象了一個場景,其中有三根繩子,每根繩子的兩端分別連線到兩個柱子上。範德蒙的研究興趣在於這些繩子在交織或編織時,如何在保持其整體結構不變的情況下進行扭曲或重組。這意味著在研究過程中,繩子不能被切斷或解開。

我們不知道是什麽促使他提出這個問題,但當時類似的問題如歐拉對柯尼斯堡七橋問題的解決方案也是一種趨勢。
那麽這一研究是如何在100年後被重新提起的呢?卡爾·佛烈德利赫·高斯提出了 連線數(linking number) 的概念,用於測量兩個封閉曲線或環在三維空間中如何交織。想象一下有兩個環A和B,
如果它們沒有接觸或交叉,連線數為零,因為它們完全獨立,沒有任何連線。現在把環B提起並透過環A的中心一次,從上方透過並從下方出來,然後再環回到頂部 ,在這種情況下,連線數是+1或-1,如何確定哪個呢?

在繼續之前,我估計絕大多數人並不理解上面藍色字型所表達的意思(或操作過程),疑惑的點在於「環是否可以切斷? 」,答案是可以的,操作也非常簡單:把B環從某處扯斷,形成一根繩子,繩子從A環穿過一次,在把繩兩端拼接起來。

我們繼續,如何確定連線數是+1,還是-1?首先,為每個環確定一個方向,比如總是順時針或總是逆時針。

如果從你的角度看頂部環從右到左交叉底部環,那麽這就是正交叉;如果從左到右交叉,這是負交叉。因為環B從環A下方透過並從左到右出現,這是負交叉或-1。

總連線數是這些交叉點的計算總和,所以如果有幾個交叉點,就將它們加起來得到最終的數位。

高斯研究這個問題的動機是什麽呢?高斯在研究積分時引入了連線數,測量兩個封閉曲線如何在空間中相互影響。
它成為拓撲學和繩結理論的基本內容。
那麽,什麽時候我們開始將這個領域稱為扭結(繩結)理論的呢?
有幾件事情發生了。首先, 流體動力學 (fluid dynamics)和 渦流行為 (vortex behaviors)成為了主流,
赫爾曼·馮·亥姆霍茲在這方面做出了重要貢獻,這些理論又影響了威廉·湯姆森(克耳文勛爵),他提出原子可以被建模為以太中的結渦管。
結渦管(knotted vortex tubes)是一種在流體力學和物理學中出現的概念,主要涉及渦旋在流體中形成復雜且閉合的繩結狀結構。渦旋通常是流體中的一個旋轉區域,而當這些旋轉的流體形成閉合的環狀結構時,它們可以呈現出類似數學繩結的形狀。

顯然,現在我們知道這是錯誤的,但當時它啟發了繩結理論之父,彼得·格思裏·泰特(Peter Guthrie Tait)。泰特在湯瑪斯·彭寧頓·柯克曼(Thomas Penyngton Kirkman)的影響下,首先系統地分類和編制了繩結,

並在1877年發表的【愛丁堡皇家學會會刊】中將其作為一個獨立的數學學科。因此,他建立了第一個全面的繩結表,這些表格基於繩結的內容和復雜性進行分類。他使用了諸如計算最少交叉點數的方法來區分不同的繩結。泰特的工作包括提出了 泰特猜想(Tait's Conjectures) ,
泰特猜想主要涉及圖論中的圖嵌入和結理論,以下是幾個著名的Tait猜想:
四面體圖猜想(Four Color Theorem): Tait最早提出的猜想之一,他猜測在平面圖中使用四種顏色可以使得每個相鄰的區域具有不同的顏色。這個猜想後來在1976年由Kenneth Appel和Wolfgang Haken透過電腦輔助證明被解決。
交替結猜想(Tait's Conjecture on Alternating Knots): Tait猜測任何一個交替結的映像具有相同的交替表示。這一猜想在20世紀20年代由Kurt Reidemeister證明。
從根本上說,泰特是第一個將繩結理論作為一個獨立的數學學科進行分類的人。
當然,克耳文的理論被否定了,因為我們發現原子並不是這樣的,但對繩結理論的數學研究仍然在獨立地發展。詹姆士·克拉克·馬克士威進一步擴充套件了泰特的「繩結表」,但接下來的一大進步是庫爾特·賴德邁斯特在1926年提出了 賴德邁斯特移動 (Reidemeister moves),這成了繩結理論研究的基石。
賴德邁斯特移動非常重要, 因為它們提供了一種方法來確定兩個繩結圖是否表示相同的繩結。 如果你可以透過只使用這些移動並多次套用,將一個圖轉換為另一個,那麽這兩個圖就被認為表示相同的繩結。
賴德邁斯特確定了三種基本操作(移動),這些操作可以套用於繩結圖:

想象一下取一小段繩子,將其扭曲成一個環,使得繩子在某處交叉,一部份在另一部份的上方或下方。


本質上,需要取兩條平行的線段,要麽透過將一條拉過另一條來將它們分開,要麽使它們靠攏,以便一條跨過另一條。

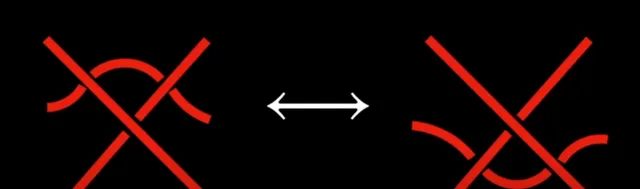
本質上,需要將繩結的一部份滑過由另外兩部碎形成的交叉點或X點。
為什麽我們需要這些操作呢?賴德邁斯特移動很強大,因為它們允許數學家在不改變繩結實際結構的情況下探索繩結的基本內容。 透過套用這些移動,我們可以簡化或改變繩結圖的外觀,同時保持繩結的重要內容,這對分析和分類繩結至關重要。
還有一種稱為 繩結不變量(Knot Invariants) 的發展,有著相同的目的。賴德邁斯特移動和繩結不變量透過不同的方法分析繩結的內容,並行揮不同的作用。
詹姆士·亞歷山大在1923年引入了 亞歷山大多項式 (Alexander Polynomial),讓我們以 三葉結(Trifoil knot) 為例,
這是最簡單的 非平凡繩結 ,因為它不能在不切割的情況下被解成一個簡單的環 。亞歷山大多項式有助於將三葉結與簡單繩結如簡單環和其他更復雜的繩結區分開來。因此,如果有兩個繩結,它們的亞歷山大多項式不同,那麽它們不是同一個繩結。簡單環的亞歷山大多項式是1,即Δ(t) = 1,而三葉結的多項式是
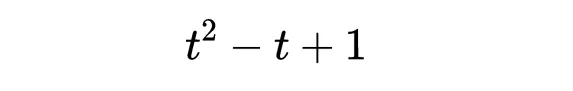
這證實了三葉結確實是一個非平凡結。
亞歷山大多項式是對稱的,當你用1/t代替t,
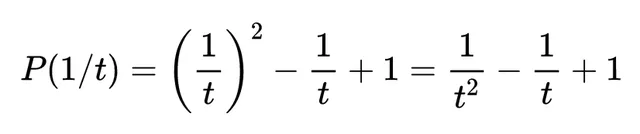
然後乘以多項式的最高次項t^2,
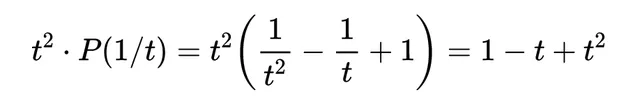
這表明三葉結是 手性對稱的 ,具有一種特定的對稱性。所以,它們用於研究和理解繩結的深層內容,超越了它們的視覺表示。
1984年,佛漢·瓊斯引入了 瓊斯多項式 (Jones Polynomial),這是一個強大的突破。它是一種繩結不變量,類似於亞歷山大多項式,但能夠捕捉到繩結和鏈條的更細微特征。佛漢·瓊斯在研究馮·紐曼代數時發展了瓊斯多項式,這完全是數學的另一個領域,但它最終對繩結理論具有突破性意義。
它是如何發展的呢?瓊斯多項式涉及分析繩結圖或繩結的繪制方式。第一步是看繩結的圖,特別是關註交叉點,繩結的一部份與另一部份交叉的地方。對於繩結圖中的每個交叉點,套用某些規則,可以改變交叉或考慮線條可能透過或在彼此下方的不同方式。每個不同的排列或狀態分別考慮。每個狀態都賦予一個代數運算式,這個運算式取決於交叉的方向,即線條是在上方還是在下方。
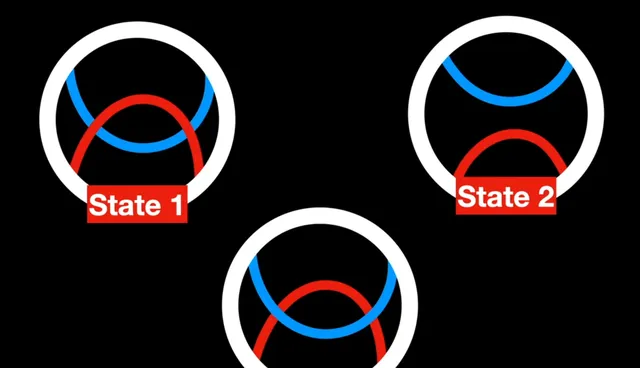
最終的瓊斯多項式是透過組合這些狀態的代數運算式得到的,
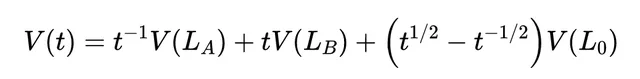
它與拓撲學的發展是如何聯系但又獨立的呢?一個很好的例子是 雙曲繩結理論(Hyperbolic Knot Theory) ,這是一個結合拓撲學、幾何學和群論的領域,主要歸功於威廉·瑟斯頓在1970年代和1980年代的工作。在瑟斯頓的工作之前,繩結理論主要研究三維空間中的繩結和鏈條。然而,瑟斯頓引入了透過雙曲幾何理解大多數繩結和流形的概念 。
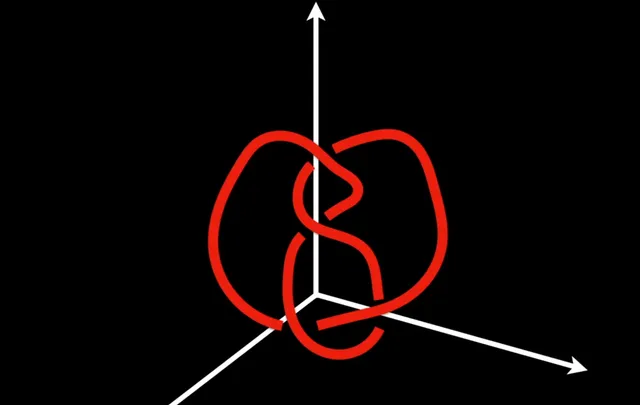
如果一個繩結的周圍空間適合套用雙曲幾何,即該空間可以定義為具有恒定的負曲率,那麽這樣的繩結稱為雙曲繩結,其周圍空間因此形成一個雙曲流形。
這些繩結限於三維空間,是否發展到其他領域呢? 虛繩結 (Virtual Knots)由路易士·考夫曼在1999年引入,這是一個非常重要的發展,因為它允許在傳統三維空間之外探索繩結。虛繩結的一個關鍵特征是它們包括虛交叉,這些不是實際的交叉,而是指示在更復雜的表面上可能發生的交叉。這些是在繩結圖中標記的不同於經典交叉的交叉點,它們不代表一個上下關系,而是表示在沒有額外背景的平面中無法表示的交叉資訊。
事情還沒有結束, 科萬諾夫同調 (Khovanov Homology)在2000年由米哈伊爾·科萬諾夫引入,這擴充套件了瓊斯多項式的概念,提供了關於繩結的更豐富資訊。它涉及構建一個與繩結圖相關的鏈復形,
每個鏈圖中的連結貢獻一個分級模,一個數學結構,這些模透過微分連結。透過套用同調代數技術,包括鏈復形的同調,科萬諾夫提取出分類瓊斯多項式的不變量。科萬諾夫同調將繩結理論與代數幾何、範疇論和同調代數等其他數學領域聯系起來。
扭結理論作為數學、物理學、化學和生物學等多個學科的交匯點,為這些領域之間提供了共同的語言和工具。例如,扭結理論在理解量子場論中的拓撲缺陷、DNA分子的結構變化以及化學中分子結合的動態中起著核心作用。











