梯度、散度、旋度是數學中的一個重要概念,在固體力學、流體力學、光學、電磁學等也有廣泛的套用。本文旨在透過聯系一些物理知識的學習,讓大家更能深刻的理解梯度、散度和旋度。本文大致分為兩部份,第一部份為一些相關數學知識學習,第二部份為相關物理知識介紹,希望對你有所幫助。
一、方精靈數與梯度
1.數學定義。
方精靈數本質上研究的是函式在某點處沿某特定方向上的變化率問題,而梯度反映的是空間變量變化趨勢的最大值和方向。
以二元函式為例,方精靈數的數學定義為:設函式z=f(x,y)在點P0(x0,y0)的某鄰域U(P0)內有定義。自點P0引射線l,與x軸正向的夾角為α,如圖所示。
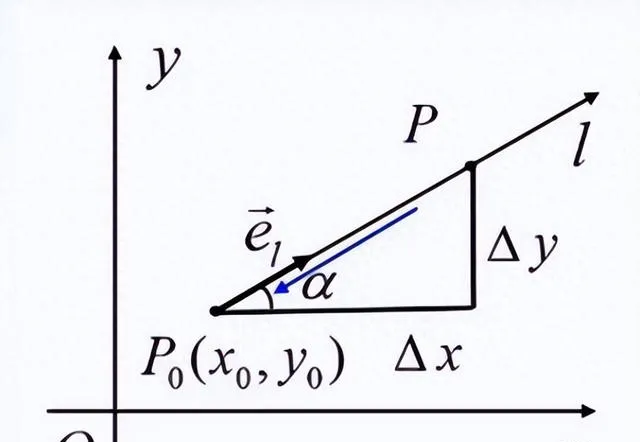
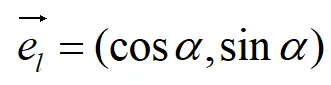
與射線l的同方向的單位向量
在l上任取一點P∈U(P0),座標為:(x0+tcosα,y0+sinα)。當P沿著l趨於P0,即t→0+時,若如下極限存在,即:
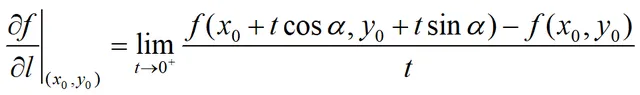
則稱此極限為函式在點P0沿方向l的方精靈數。如果函式z=f(x,y)在點P0(x0,y0)處可微,則函式在點P0(x0,y0)沿任何方向的方精靈數均存在且有:
其中cosα,cosβ為射線l與x軸和y軸的方向余弦。以上結論可推廣到三元及以上的多元函式。即:
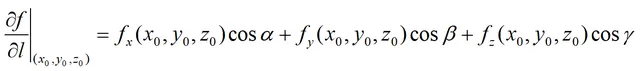
梯度的定義為:設函式z=f(x,y,z)在定義區域Ω內具有一階連續的偏導數,對於區域Ω內的任意一點(x0,y0,z0),對應的向量:
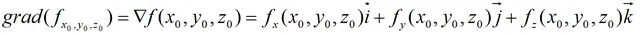
稱為函式z=f(x,y,z)在點(x0,y0,z0)處的梯度向量,簡稱為梯度。其中▽稱為哈密頓算子。
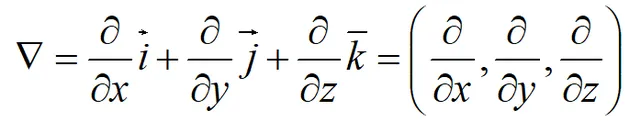
方精靈數與梯度有如下關系:
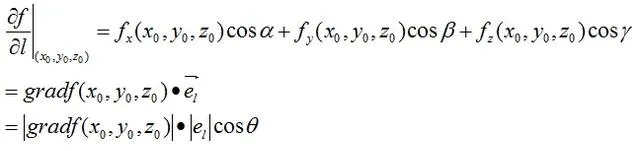
其中向量el為射線l的單位向量
顯然:當射線l的方向與梯度方向一致時,方精靈數取最大值,即梯度方向是函式增長速度最快的方向。當射線l的方向與梯度方向垂直時,方精靈數在垂直於梯度的方向上值為零,即在此方向上函式的變化率為零。當射線l的方向與梯度方向相反時,方精靈數取最小值。
2.方精靈數與梯度的物理意義。
學完了大家是不是還是有點暈,這一堆公式到底表示什麽呢?下面我們借助一些物理上保守力和勢能的知識在進行說明,可能大家會有一些不一樣的收獲。
保守力是指其對物體做功只與物體的始末相對位置有關,和路徑無關的力。典型的保守力有重力、彈力、萬有重力和靜電場力等。
勢能是物體由於位置或位形而具有的能量,也可以釋放或者或者轉化為其他形式的能量。勢能屬於系統,是狀態量,又稱位能。可以規定某位置或位形為0勢能位置,勢能0點的選擇和參考系無關。力學中勢能主要有重力勢能和彈力勢能等。
二者間有如下的關系:系統的保守力所作的功等於系統勢能減少,或等於系統勢能增量的負值。即:
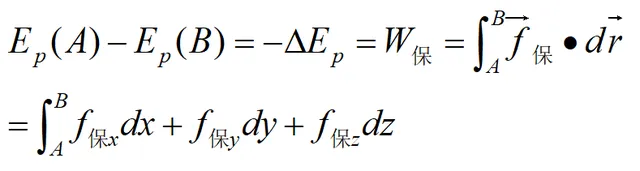
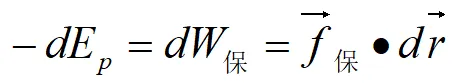
微碎形式
反過來也可以由勢能來求保守力。已知一質點受保守力,並沿某一方向移動,如下圖,則保守力所作功和勢能的關系如下:
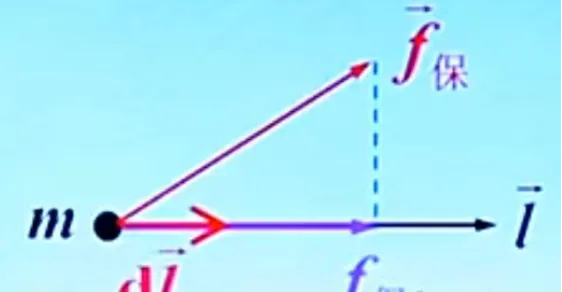
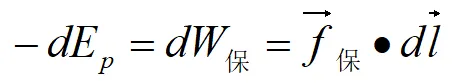
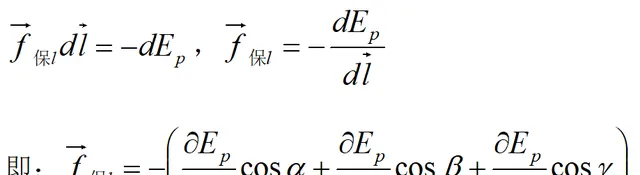
即在某點處,保守力沿空間某一方向的分量等於勢能沿該方向的方精靈數的負值。
顯然當方向l與f保的方向一致或相反時,f保的分量的絕對值就是f保,達到最大。這與梯度的定義完全一致。
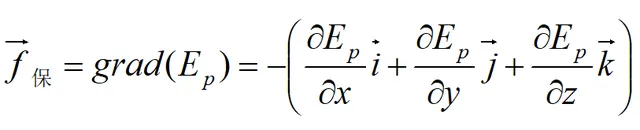
現在還需要解決一個問題,為什麽保守力一定會存在一個對應的勢函式呢?這是由於保守力做功與路徑無關。這讓我們想到了數學中對座標的曲線積分與路徑無關的四個等價條件的定理。設G是空間一維單連通域,函式P(x,y,z),Q(x,y,z),R(x,y,z)在G內具有一階連續偏導數,則對於G內任意一點,如下四個條件是等價的。
1.對G內任一分段光滑曲線l,如下積分
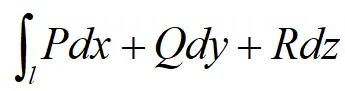
與路徑無關。
2.若l是G任一分段光滑閉曲線,則:
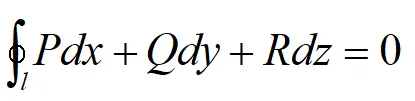
3.如下等式成立:
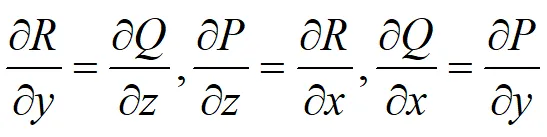
4.Pdx+Qdy+Rdz在G內是某一函式u(x,y,z)的全微分。
所以根據條件2,可得到一個推論:保守力沿任意閉合路徑做功為零。
根據條件4,保守力做功與路徑無關,必然存在:
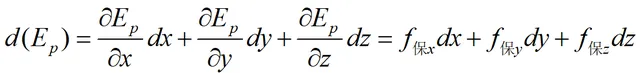
所以保守力必然存在一個勢函式(純量函式)與之對應。
二、通量與散度。
1.數學定義。
設有向量場:
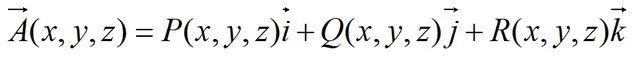
函式P(x,y,z),Q(x,y,z),R(x,y,z)有一階連續偏導數,曲面Σ為場內的一片有向光滑曲面,n為Σ上的某一M(x,y,z)處的單位法向量。對面積的曲面積分:
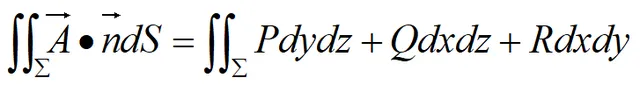
稱為向量場A透過有向曲面Σ的通量(或流量)。
對向量場內任意一點M(x,y,z),數量函式:

稱為向量場A在點M的散度。
2.通量與散度的物理意義。
通量的物理解釋:即對穩定流動的不可壓縮流體,速度場為:
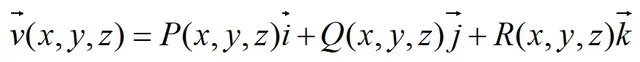
Σ為場中任一有向曲面,如下圖:
則單位時間透過曲面Σ的流量為:
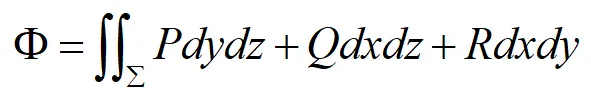
由兩類曲面積分的關系可知,流量還可表示為:
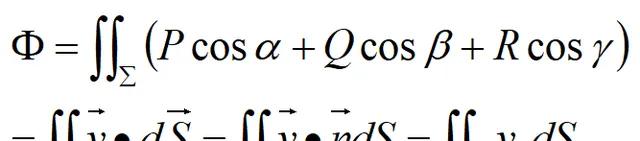
其中:vn為速度v在曲面法向量的投影。
散度的物理意義:令M(x,y,z)是某一流體流速場中任意一點,不難求得:
其中Φ表示透過速度場內某一封閉區域Ω的邊界屈面Σ的通量。
根據高斯公式,上式可得:
根據積分均值定理,存在一點(ξ,η,ζ)∈Ω使得下式成立。
此式也給出了散度的另外一種解釋,即散度是通量對體積的變化率,反應了流速場在點M的特點:散度值為正,負或0,分別反映在該點有流體湧出,吸入或沒有任何變化。綜上可知,散度是通量對體積的變化率,且有:
表明在該點處有流體流出,稱之為源。
表明在該點處有流體被吸入,稱之為匯。
表明在該點處無源無匯。
而散度的絕對值反映了源的強度。
三、環流量與旋度。
1.數學定義。
設有向量場:
函式P(x,y,z),Q(x,y,z),R(x,y,z)有一階連續偏導時。Γ是向量場A的定義域內一條分段光滑封閉曲線,向量τ為曲線Γ在點(x,y,z)處的單位切向量,則向量場A中沿封閉曲線Γ上的曲線積分,稱為向量場A沿有向閉曲線Γ的環流量。如下式:
以向量場A在座標軸上的投影有關偏導式:
作為分量的向量稱為向量場A的旋度,記作:
設曲面Σ是由Γ張成的一片有向光滑曲面,利用斯托克斯公式、兩類曲線積分以及兩類曲面積分的關系,向量場A的環流量和旋度有如下關系:
2.環流量與旋度的物理意義。
以平面流體為例,根據環流量的定義設有一平面流速場v在單位時間沿閉曲線L的環流量為:
其中:向量τ為曲線L某點的單位切向量,向量n為曲線L某點的單位切向量。
值得註意的是:我們一定要區分環流量與通量(流量)。環流量是流速沿切線方向對弧長的積分。而通量(流量)嚴格定義是曲面積分,但對於平面流體,可以理解為流速沿法線方向對弧長的積分,即上述流速場對於曲線L的通量Φ為:
旋度的物理意義:設某剛體繞定軸l轉動,角速度向量為ω,M為剛體上任意一點,建立如圖所示的座標系:
則有:
點M的線速度
點M的旋度
也即旋度是角速度的2倍,同樣該結論同樣可以推廣到三維空間。這也是「旋度」一詞的來源。
下面再以一個例子直觀的理解一下旋度的含義。
首先我們建立一個二維平面,即xy平面。假設速度場沿x方向速度分量是P(x,y)i,沿y方向的速度分量是Q(x,y)。xy平面中有一剛體。當x方向速度分量P(x,y)=0,y方向的速度分量Q(x,y)=常數時,如下圖:
大家可以發現剛體將沿著平行於Y軸的方向運動,而不會發生旋轉,那麽我們說剛體的旋度是0。即:
即速度沿著剛體的方向x發生變化時,剛體將產生旋轉,如下圖:
四、哈密頓算子。
最後再談一下前面提到過的哈密頓算子,哈密頓算子的引入可以使許多運算式顯得簡潔、美觀,在數學、物理等都有廣泛的用途。例如:
設f(x,y,z)為一函式,則梯度可表示為:
表示哈密頓算子作用於某一純量函式
設f(x,y,z)為一向量函式,f(x,y,z)=[P(x,y,z),Q(x,y,z),R(x,y,z)],則散度可表示為:
表示哈密頓算子與一向量函式的點積
設f(x,y,z)為一向量函式,f(x,y,z)=[P(x,y,z),Q(x,y,z),R(x,y,z)],則旋度可表示為:
表示哈密頓算子與一向量函式的叉積
梯度、散度、旋度的運算也表示了哈密頓算子的三個作用,即作用於純量函式,與向量函式點積或叉積,可得到不同物理含義的運算式。
本文完,感謝你的耐心閱讀。











