上一篇給出了常數e和π是無理數的證明,前面說了 超越數的證明比無理數的證明要困難地多 ,100年後,1873年法國數學家埃爾米特證明了e是超越數,其過程中的一個定理後來發展成著名的 林德曼-魏爾斯特拉斯 定理,這個定理的強大之處在於可以證明一系列數是超越數,從而讓e和π的超越性可由該定理直接匯出。回憶前面證明e是無理數的方法,是根據一個e的無窮級數,利用反證法假設e是有理數,即可建立關於有理數的方程式,而有理數經通分就是整數,所以最終是 透過關於整數的方程式推出矛盾 。證明超越性的困難在於,假設e是代數數,它是某一多項式的根,無法像有理數一樣把它寫成兩個整數之比。

我記得有數學家說過, 要是缺點靈感,就去讀讀19世紀的數學 。我覺得學習數學,不能拋開數學的發展史。在西方, 數學專業拿的是文學學士 ,這也佐證了我的一個觀點。 相比數學和科學的距離,我認為數學離文學更近 。數學中所研究的物件並不是自然界存在的物件,而是人的意識所創造的。所以很多科普博主是把數學和物理、化學甚至工科中的人工智慧融在一起,而 我更傾向於將數學和文學、心理學相融合 ,這也意味著我所介紹的數學是純粹數學而不會是套用數學。 數學研究有其邏輯的成分也有其直覺的部份 。從心理學榮格八維的角度看,有的人是直覺主導、有的人是邏輯主導,他們所呈現的數學也是不同的。我個人是直覺先於邏輯,所以更傾向於一針見血直指本質的內容。下面介紹如何證明e是超越數,所用的證明方法比較初等,只需會一點微積分就可以理解。
證明 :反證法,假設e為某個n次整系數多項式g(x)的根,
接下來一步很關鍵,對於任意的多項式p(x),假設最高次為r,構造多項式P(x),

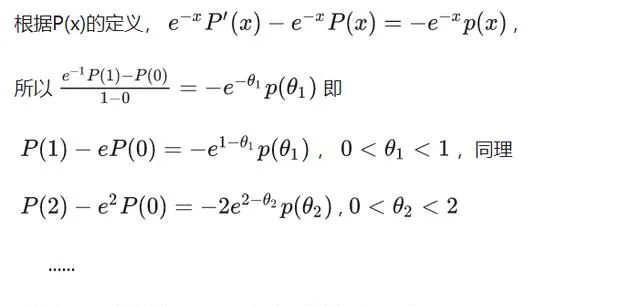

到這兒,我們的證明已經完成百分之八十了,後面只是一個技術性的驗證。很多時候我們看別人的證明能看懂,但是自己卻不能找到證明的方向,這是為什麽? 那就是沒有思考別人為什麽要這樣做 ?數學家為何要構造P(x)這樣的多項式?註意 上式是個恒等式,也就是不論e是不是超越數上式都成立 。只不過當e是超越數時,其中的式子

只要e是超越數,這個式子必然能推出矛盾 。現在的問題是透過什麽方式推出矛盾。回憶證明e是無理數的過程,透過等式兩邊一個是整數一個是小數推出矛盾。有的讀者會思考,存不存在兩邊是不同整數的情況,使我們推不出矛盾。這種情況不存在,因為 若e是超越數,將它代入到整系數多項式裏一定是小數 ,若是整數,那我們讓這個多項式減去該整數,還是個整系數多項式,那麽e就不是超越數了。
這個多項式的特點是1,2,...,n處是q重根,在0處是q-1重根,可以推出(1)式左邊是個 非0整數 。最後的工作就是推出右邊是個小於1的數了,比較簡單留給讀者思考。

在e是超越數被證明之後,林德曼很快證明了π是超越數,沿用了埃爾米特的方法, e和iπ透過一個很經典的公式歐拉公式聯系起來 ,林德曼證明了iπ是超越數,那麽π必然是超越數了。
再過了幾年,一個更一般的結論出現了,由它可以匯出一系列數是超越數,它就是 林德曼-魏爾斯特拉斯定理 。

隨著π是超越數被證明,困擾人類幾千年的數學問題 化圓為方 問題被徹底解決。











