
統計學是數據分析的基礎理論,但統計結論往往存在一些"坑"。面對統計結果,我們需要仔細分析和避免常見的錯誤,其中包括將數理關系誤認為因果關系、不同變量之間可能存在悖論,以及數據統計可能受到偏差的影響。
在眾多悖論中,伯克森悖論( Berkson's Paradox )是其中之一。它指出在處理數據時,容易因為未能全面了解整個情況而誤以為兩個事物存在關聯。這種錯誤可能對機器學習專家的預測模型準確性產生重大影響,因為它導致了對變量之間關系的錯誤假設。
透過一個例子來解釋,例如,我們假設某學生的文化成績較高,那麽他的體育成績就較差;反之,體育成績越好,文化成績就越差。這似乎已經成為我們日常觀察中的一種認知,即班上的尖子生好像體育成績普遍不太出色。那麽,這種現象是如何出現的呢?
設想學生需要參加兩種型別的考試,即文化和體育課,其中只要在任何一種型別的考試中獲得90分以上就能順利畢業。因此,畢業的學生要麽在文化考試中取得90分以上,或者在體育考試中獲得90分以上,或者在兩門考試中都取得90分以上。通常情況下,正常人只需專註於其中一門考試,充分發揮至極致即可,而對另一門考試不太重視。因此,學生的文化成績和體育成績會呈現負相關的關系。
伯克森悖論還能解釋為什麽很多人都認為帥哥通常是渣男,以及為什麽顏值超高的小鮮肉演員演技不盡人意,這些現象。
舉個數值事例說明伯克森悖論
為了說明伯克森悖論( Berkson's Paradox ),接下來使用兩個骰子:
這兩個事件顯然是獨立的,其中 P(X)=1/6 而 P(Y)=1/3。
現在,讓我們引入條件(Z),表示透過 第一個骰子是 6 點且第二個骰子是 1 點或 2 點的所有結果而引入的抽樣偏差。
在我們的有偏抽樣條件下,我們需要計算事件 X 發生的機率,假設至少其中一個事件(X 或 Y)發生,這由 P(X|Z) 表示。
首先,我們需要確定 Z = (X ∪ Y) 的機率(即在已知第一個骰子是 6 點或第二個骰子是 1 點或 2 點的情況下,第一個骰子出現 6 點的機率):
P(Z)=P(X∪Y)
=P(X)+P(Y)−P(X∩Y)
=P(X)+P(Y)-P(X)×P(Y)
=1/6+1/3-1/6×1/3
=4/9
接下來,我們計算給定 Z 的 X 的機率:
P ( X ∣ Z ) =P(X∩Z)/P(Z)=P(X)/P(Z)
=1/6 / (4/9)
=3/8
=0.375
為了檢視在 Z 發生的假設下 X 和 Y 之間是否存在依賴關系,我們必須計算(已知第二個骰子是 1 點或 2 點的情況下,同時第一個骰子是 6 點的情況下,第一個骰子出現 6 點的機率):
P(X | Y ∩ Z) ≈ 0.1666…
上述數據確實得到了伯克森悖論的特性,由於抽樣偏差 Z,我們有 P(X | Z) > P(X ∣ Y ∩ Z)。
是不是這相當令人驚訝!我們有兩個骰子…兩個明顯獨立的隨機事件…透過一個抽樣過程,我們會產生骰子點數變得相互依賴的印象。
Python模擬擲骰子的過程復現伯克森悖論
在下面的程式碼中使用Python模擬擲骰子的過程。
以下程式碼模擬了一百萬次擲兩個骰子的實驗,在每次實驗中,它檢查第一個骰子是否擲出6點(事件X),以及第二個骰子是否擲出1點或2點(事件Y)。然後,它將這些檢查的結果(True或False)分別儲存在列表X和Y中。
import randomdef sample_X_Y(nb_exp): X = [] Y = [] for i in range(nb_exp): dice1 = random.randint(1,6) dice2 = random.randint(1,6) X.append(dice1 == 6) Y.append(dice2 in [1,2]) return X, Ynb_exp=1_000_000X, Y = sample_X_Y(nb_exp)
以下程式碼計算了事件X的機率和在事件Y發生的條件下事件X的條件機率。它透過將成功的結果數量除以每個機率的總實驗次數來完成這個計算。
p_X = sum(X)/nb_expp_X_Y = sum([X[i] for i in range(nb_exp) if Y[i]])/sum(Y)print("P(X=1) = ", round(p_X,5))print("P(X=1|Y=1) = ", round(p_X_Y,5))
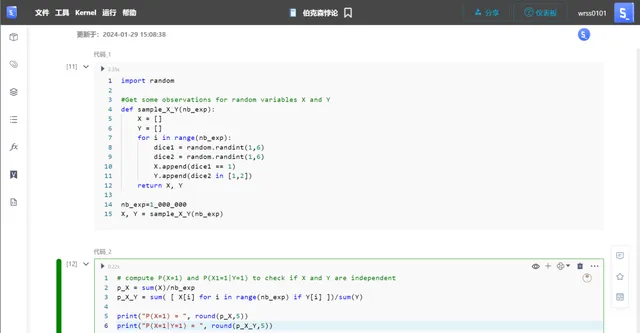
正如所看到的,這兩個機率是接近的;因此兩個骰子是獨立的。
現在,讓我們看看在引入抽樣偏差Z時會發生什麽。下面的程式碼過濾了實驗的結果,僅保留那些其中X = 1,Y = 1或兩者都為1的結果。它將這些過濾後的結果儲存在列表XZ和YZ中。
XZ = []YZ = []for i in range(nb_exp): if X[i] or Y[i]: XZ.append(X[i]) YZ.append(Y[i]) nb_obs_Z = len(XZ)
現在,檢查一下這些新變量是否仍然是獨立的。
p_X_Z = sum(XZ)/nb_obs_Zp_X_Y_Z = sum([XZ[i] for i in range(nb_obs_Z) if YZ[i]])/sum(YZ)print("P(X=1|Z=1) = ", round(p_X_Z,5))print("P(X=1|Y=1,Z=1) = ", round(p_X_Y_Z,5))
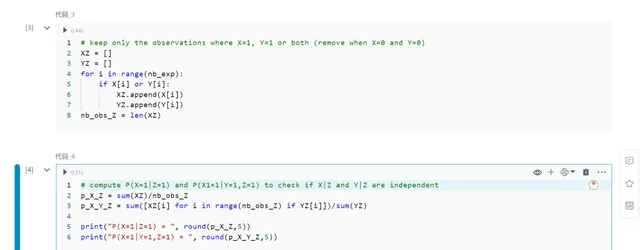
這意味著如果Z為真,則擁有關於Y的資訊會改變X的機率;因此,它們不再是獨立的。
伯克森悖論悖論對機器學習的影響
現實中,數據科學家或演算法工程師們並沒有足夠關註這種型別的偏差。伯克森悖論悖論涉及到了我們如何被我們使用的數據誤導的問題。伯克森悖論警告我們關於使用有偏或片面數據的危險。
在每種情景中,忽視伯克森悖論可能導致有偏的模型,影響決策和公平性。機器學習專家必須透過多樣化資料來源並不斷驗證模型與實際場景相匹配,以抵消這種影響。
總而言之,伯克森悖論是機器學習專業人士提醒他們審查數據來源並避免誤導性相關性的重要提醒。透過理解和考慮這一悖論,可以構建更準確、公平胡實用的模型,真正反映現實世界的復雜性。記住,健壯的機器學習關鍵在於精密的演算法和對數據的深思熟慮、全面的收集與分析。











