這裏的X是一個集合，R是X上的一個σ代數。
意思是說，集合Ā是由集合A再並上集合E構成的，而且集合E的測度為0。
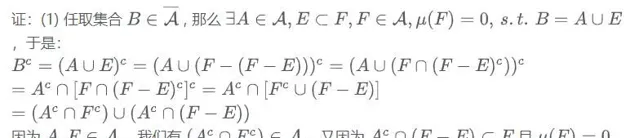
以上內容不難理解。
以上是把集合B拆分為無窮多個，結論仍然成立。
這個定理的意思就是，當A這個σ代數再加上測度為0的集合以後，還是一個測度空間。
比如，假設X是無理數集合，A是X上的一個σ代數。這個時候如果再把有理數加入集合A構成集合Ā，則(X,Ā)還是一個測度空間。
這個定理是測度擴張的基礎。
測度擴張的一個基礎定理
這裏的X是一個集合，R是X上的一個σ代數。
意思是說，集合Ā是由集合A再並上集合E構成的，而且集合E的測度為0。
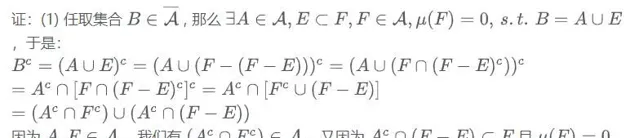
以上內容不難理解。
以上是把集合B拆分為無窮多個，結論仍然成立。
這個定理的意思就是，當A這個σ代數再加上測度為0的集合以後，還是一個測度空間。
比如，假設X是無理數集合，A是X上的一個σ代數。這個時候如果再把有理數加入集合A構成集合Ā，則(X,Ā)還是一個測度空間。
這個定理是測度擴張的基礎。
Copyright © 2024 www.aqiusha.com NO.1 華文世界
商務合作：xingwa#jasve.com（傳送郵件請將#換成@）
