编辑:润
【新智元导读】 由Transformer论文作者创立的Adept AI推出了号称仅次于GPT-4V和Gemini Ultra的多模态大模型Fuyu-Heavy。它不但有精准识别图片,特别是UI的能力,数理推理能力也非常强。
2024年果然是大模型的多模态之年。
又有一家独角兽Adept AI推出了他们的多模态大模型Fuyu-Heavy。
这家由两位从谷歌出走的Transformer论文作者创立的Adept AI,目标是开发一个提升打工人工作效率的AI智能体。
而Fuyu-Heavy就是驱动他们未来即将推出的智能体产品的基础多模态大模型。
他们宣称,Fuyu-Heavy是除了GPT-4V和还没有面世的Gemini Ultra之外,是目前最强大的多模态大模型。
而且它的尺寸大小还不到前面两者的10%。
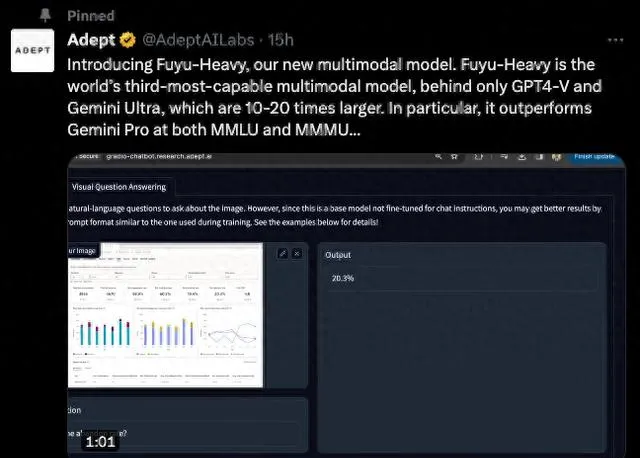
-它擅长多模态推理。对我们来说,杀手级功能是UI理解,但它在更传统的多模式基准测试中也表现良好。特别是,Fuyu-Heavy 在 MMMU 基准测试中的得分比Gemini Pro还要高。
-在标准的基于文本的基准测试中,尽管Fuyu-Heavy必须将其部分能力空间留给图像模块,但它的性能仍可以超过同级别模型的性能。
因为Adept AI最优先的产品目标受众是企业用户,他们致力于开发一个能在办公场所大大提高工作效率的AI智能体,所以他们专门还训练了Fuyu-Heavy的UI理解能力。
而且按照Adept的说法,Fuyu-Heavy有非常强的数理推理能力,能够在多模态的任务中充分发挥数理能力,为此他们专门展示了一道「行测」题:
提示词:
根据下表,哪些食物最有可能引发食物中毒

Fuyu-Heavy输出:
该表显示了吃了不同食物的人数以及吃了这些食物而生病的人数。为了确定哪种食物最有可能导致食物中毒爆发,我们正在寻找食用该食物并患病的人比例最高的食物。
让我们计算一下吃了每种食物并生病的人的百分比:
凉拌鸡:34 / 86 = 0.395,即39.5%
土豆沙拉:38 / 54 = 0.704,即70.4%
鸡蛋三明治:40 / 76 = 0.526,即 52.6%
水果派和奶油:12 / 32 = 0.375,即 37.5%
奶酪:12 / 48 = 0.25,即 25%
吃了该食物而生病的人比例最高的食物是土豆沙拉,占70.4%。因此,土豆沙拉是最有可能引发食物中毒的原因。
Fuyu-Heavy是如何诞生的
在去年10月份,Adept推出了自己的基础模型Fuyu-8B,是一个非常简洁高效,而且能力强大的原生多模态模型。
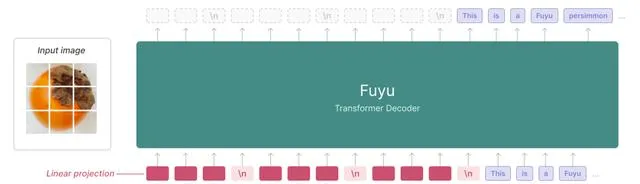
在Fuyu-8B的基础之上,Adept花了4个月的时间不断扩大模型的规模和能力。
除了模型缩放定律有关的标准问题之外,他们还必须处理原生的多模态大模型在文本和图像数据上与构架相关的各种问题。
图像数据给模型带来压力——给多模态模型喂数据会很困难:内存使用量激增,云存储入口/出口受到限制;即使在训练和推理之间一致地处理图像格式/坐标也是很麻烦的问题。
图像模型是出了名的不稳定——所以他们不得不对Fuyu的架构和训练过程进行了大幅调整,来应对这个问题。
而且,高质量的图像预训练数据是非常稀缺的,他们投入了大量的精力来收集、整理甚至创建这些数据。文本和图像任务之间也存在微妙的平衡,文本数据太多,图像性能就会下降,反之亦然——必须找到合适的方法来大规模地实现这种平衡。
通过4个月的努力,在解决了这些问题之后,Adept推出了Fuyu-Heavy,同时很快将会推出基于这个模型的产品。
测评成绩
按照Adept的说法,Fuyu-Heavy的性能是仅次于GPT-4V和Gemini Ultra的多模态大模型。
如果单纯评估文本能力,它的性能和Gemini Pro大致相当。

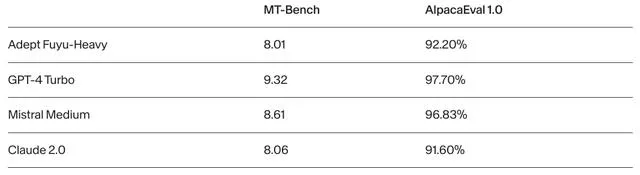
在评估长对话能力的MT-Bench和AlpacaEval 1.0上,Fuyu-Heavy的性能超过了Claude 2。
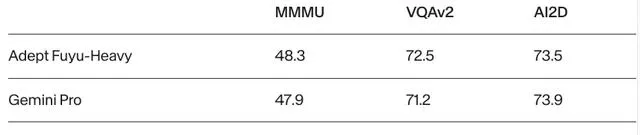
而在评估模型多模态性能的MMMU上,Fuyu-Heavy表现出了超过Gemini Pro的能力。
惊人的多模态推理能力
Adept还分享了Fuyu-Heavy回答MMMU问题的案例。
Janet Ludlow的公司要求所有分析师使用两阶段股息贴现模型 DDM和资本资产定价模型 CAPM来对股票进行估值。
Ludlow使用CAPM和DDM对QuickBrush公司的估值为每股63美元。
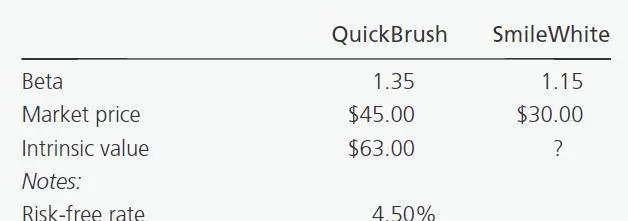
她现在必须重视 SmileWhite 公司。使用下表中的信息计算 SmileWhite 要求回报率:
Adept回复:
SmileWhite的所需回报率可以使用资本资产定价模型(CAPM)计算,即:
要求回报=无风险利率+Beta x(预期市场回报-无风险利率)
表中提供了无风险利率和预期市场回报,SmileWhite 的贝塔值为 1.15。
让我们计算一下 SmileWhite 所需的回报率:
要求回报率 = 4.50% + 1.15 x (14.50% - 4.50%)
要求回报率 = 4.50% + 1.15 x 10%
要求回报率 = 4.50% + 11.50%= 16%
Fuyu-Heavy还可以执行更加复杂的计算:
表 11.47 提供了最近对净资产估计为 100 万美元或以上的最年轻在线企业家的调查。他们的年龄范围从17岁到30岁。表中的每个单元格说明了与特定年龄组相对应的企业家数量及其净资产。我们想知道年龄和净资产是否独立。
求出$$\ch$$^2 test statistic为多少?
Adept回复:
为了回答这个问题,我们需要进行独立性的chi-square测试。
该检验的原假设是年龄和净资产是独立的,而备择假设是它们不是独立的。
chi-square独立性检验的检验统计量为:
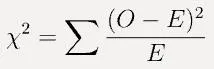
其中 O 是观察到的频率,E 是预期频率,并且对列联表中的所有单元格进行求和。
每个空格的预期频率计算如下:
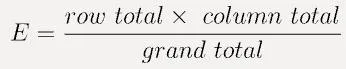
chi-square的独立性检验的自由度为:

在给定显着性水平(例如 0.05)下具有 df 自由度的chi-square分布的临界值可以在chi-square表中找到或使用统计软件包计算。
如果计算出的chi-square值大于临界值,我们拒绝零假设并得出年龄和净资产不独立的结论。如果计算出的chi-square值小于或等于临界值,我们就无法拒绝零假设并得出结论:年龄和净资产是独立的。
让我们计算表中每个单元格的预期频率:
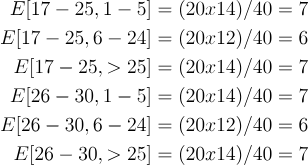
现在,我们来计算chi-square检验统计量:
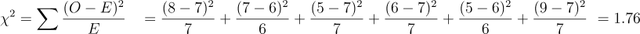
该测试的自由度为:
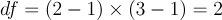
具有 2 个自由度、显着性水平为 0.05 的chi-square分布的临界值约为 5.99。
由于我们计算出的chi-square值 (1.76) 小于临界值 (5.99),因此我们无法拒绝零假设并得出结论:年龄和净资产是独立的。

这惊人的计算能力和识图准确度,让人实在是期待他们未来的智能体产品!











