算丰技术揭秘｜基于TPU-MLIR：详解EinSum的完整处理过程！

EinSum介绍

EinSum （爱因斯坦求和）是一个功能强大的算子，能够简洁高效地表示出多维算子的乘累加过程，对使用者非常友好。

本质上， EinSum是一个算子族，可以表示多种基础操作，如矩阵乘法、Reduce。EinSum支持任意多的输入，只要计算中只包含点乘（element-wise）、广播（broadcast）、归约求和（reduction sum）都可以使用EinSum来表示。以下给出一种将EinSum计算等价表达的流程：

1. 将输入的维度符号放入一个列表，移除重复元素后按升序排列；
2. 对各输入维度执行转置操作，确保维度标识符按照升序对齐，实现维度对齐；
3. 在缺失的维度上填充1（扩展维度），以便与第一步中定义的维度保持一致；
4. 对所有输入执行广播点乘；
5. 对那些不在输出标识符中的维度执行累加操作；
6. 利用转置操作调整维度顺序，使其与输出标识符的顺序一致。

下图是以 out = EinSum("ijk, lki-> li", in0, in1 ) 为例，根据上述步骤进行等价转换。

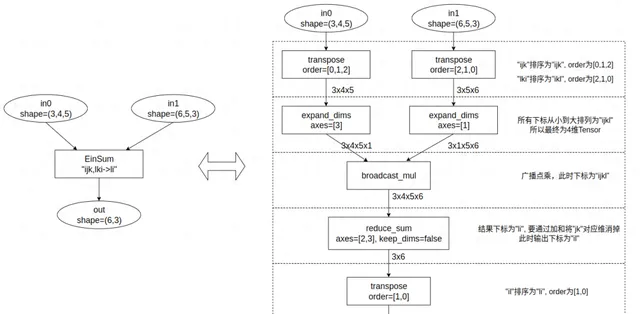
TPU-MLIR转换

虽然使用上述流程可以完成对EinSum的计算转换，但如果严格按照该流程执行，会带来大量的Transpose和Reshape操作，这不仅会给TPU-MLIR的LayerGroup功能带来挑战，同时也难以显式地识别出如矩阵乘法这类操作，从而无法充分利用硬件加速单元。因此，TPU-MLIR并未直接采用上述流程进行转换。

接下来，我们将详细介绍EinSum的完整处理过程。

前端接口

以下示例代码摘自OnnxConverter.py文件，并附带了注释。代码整体结构简洁明了，我们可以看到，转换函数目前仅支持两个输入的常见情况。特别需要注意的是公式的归一化过程。由于EinSum的表达式可以使用任意非重复字符来表示下标，这虽然提高了可读性，但也导致 同一操作有多种不同的表示方式。归一化操作就是将表达式字符重新映射，以字符'a'作为起始。例如，比如 ij,jk->ik 和 dk,kv->dv 都会映射为 ab,bc->ac 。

# https://pytorch.org/docs/1.13/generated/torch.einsum.html?highlight=einsum#torch.einsum def convert_einsum_op(self, onnx_node): assert (onnx_node.op_type == "Einsum") equation = onnx_node.attrs.get("equation").decode() # 公式归一化 def normalize_equation(equation_c): equation = equation_c new_equation = '' start = 'a' translate_map = {} for s in equation: if s == ' ': continue elif not ((s >= 'a' and s <= 'z') or (s >= 'A' and s <= 'Z')): translate_map[s] = s elif s not in translate_map: translate_map[s] = start start = chr(ord(start) + 1) new_equation += translate_map[s] return new_equation equation = normalize_equation(equation) lhs = self.getOperand(onnx_node.inputs[0]) # # 大多情况下rhs是Weight, self.getOp会先到Weight Map中查找；如果找不到， # 其会从Mutable Tensor中查找，然后返回对应的Value。 rhs = self.getOp(onnx_node.inputs[1]) new_op = top.EinsumOp(self.unranked_type, [lhs, rhs], mode=StringAttr.get(equation), # 设置 loc 信息，方便找到原图对应算子 loc=self.get_loc("{}_{}".format(onnx_node.name, onnx_node.op_type)), # 将该算子插入到当前的block中 ip=self.mlir.insert_point).output # 将输出放到Mutable Tensor列表中，供后面算子使用 self.addOperand(onnx_node.name, new_op)

内部转换

TPU-MLIR目前支持了几种常见的表达式，并根据不同的算子进行了优化转换。所有的变换最终都利用了硬件的矩阵乘法加速单元，从而实现了对算子的有效加速。以下是部分代码片段，该代码来自 tpu-mlir/lib/Dialect/Top/Canonicalize/Einsum.cpp ，并在原有基础上添加了注释。

struct ConvertEinsum : public OpRewritePattern<EinsumOp> { using OpRewritePattern::OpRewritePattern; LogicalResult matchAndRewrite(EinsumOp op, PatternRewriter &rewriter) const override { // 目前只支持输入个数为2或者输入0为Weight的情况 if (op.getInputs().size() != 2 || module::isWeight(op.getInputs()[0])) { llvm_unreachable("Not support now."); // return failure(); } auto none = module::getNoneOp(op); auto mode = op.getMode().str(); auto lhs = op.getInputs()[0]; auto rhs = op.getInputs()[1]; auto lshape = module::getShape(lhs); auto rshape = module::getShape(rhs); std::string lname = module::getName(lhs).str(); std::string rname = module::getName(rhs).str(); std::string name = module::getName(op.getOutput()).str(); std::vector<Value> operands; std::vector<NamedAttribute> attrs; if (mode == "a,b->ab") { // 外积操作: 可看作[a,1]x[1,b]的矩阵乘法操作 // lhs->ReshapeOp(): shape=[a] to shape[a,1] rewriter.setInsertionPointAfter(lhs.getDefiningOp()); // auto newType = RankedTensorType::get({lshape[0], 1}, module::getElementType(lhs)); auto loc = NameLoc::get(rewriter.getStringAttr(lname + "_to2dim")); auto lrsOp = rewriter.create<ReshapeOp>(loc, newType, ValueRange{lhs}); operands.push_back(lrsOp); // rhs->ReshapeOp(): shape=[b] to shape[1,b] rewriter.setInsertionPointAfter(rhs.getDefiningOp()); newType = RankedTensorType::get({1, rshape[0]}, module::getElementType(rhs)); loc = NameLoc::get(rewriter.getStringAttr(rname + "_to2dim")); auto rrsop = rewriter.create<ReshapeOp>(loc, newType, ValueRange{rhs}); operands.push_back(rrsop); operands.push_back(none); // 用MatMulOp实现[a,1]x[1,b]=[a,b], 并替换原来的EinSum操作 rewriter.setInsertionPoint(op); auto matmulOp = rewriter.create<MatMulOp>(op.getLoc(), op.getType(), operands, attrs); op.replaceAllUsesWith(matmulOp.getOperation()); rewriter.eraseOp(op); } else if (mode == "abcd,cde->abe") { // 可以转换成矩阵乘法[a*b, c*d]x[c*d, e]->[a*b, e]->[a,b,e] // lhs_reshape_rst = [lhs_shape[0] * lhs_shape[1], lhs_shape[2] * lhs_shape[3]] rewriter.setInsertionPointAfter(lhs.getDefiningOp()); auto newType = RankedTensorType::get({lshape[0] * lshape[1], lshape[2] * lshape[3]}, module::getElementType(lhs)); auto loc = NameLoc::get(rewriter.getStringAttr(lname + "_to2dim")); auto lrsOp = rewriter.create<ReshapeOp>(loc, newType, ValueRange{lhs}); operands.push_back(lrsOp); newType = RankedTensorType::get({rshape[0] * rshape[1], rshape[2]}, module::getElementType(rhs)); if (module::isWeight(rhs)) { rhs.setType(newType); operands.push_back(rhs); } else { rewriter.setInsertionPointAfter(rhs.getDefiningOp()); loc = NameLoc::get(rewriter.getStringAttr(rname + "_to2dim")); auto rrsop = rewriter.create<ReshapeOp>(loc, newType, ValueRange{rhs}); operands.push_back(rrsop); } operands.push_back(none); rewriter.setInsertionPoint(op); newType = RankedTensorType::get({lshape[0] * lshape[1], rshape[2]}, module::getElementType(op)); loc = NameLoc::get(rewriter.getStringAttr(name + "_matmul")); auto matmulOp = rewriter.create<MatMulOp>(loc, newType, operands, attrs); auto orsOp = rewriter.create<ReshapeOp>(op.getLoc(), op.getType(), ValueRange{matmulOp}); op.replaceAllUsesWith(orsOp.getOperation()); rewriter.eraseOp(op); } else if (mode == "abcd,bed->abce") { rewriter.setInsertionPointAfter(rhs.getDefiningOp()); // 转换过程 // batch matmul does not support broadcast // temporary solution // [h, k, c] -> [1, h, k, c] -> [b, h, k, c] operands.push_back(lhs); RankedTensorType newType; // 右操作数处理 if (auto wOp = dyn_cast<top::WeightOp>(rhs.getDefiningOp())) { // 对于Weight来说，可以将数据复制，解决不支持广播问题， [b, e, d]->[a, b, e, d] auto storage_type = module::getStorageType(rhs); assert(storage_type.isF32() && "Todo, supoort more weight type"); auto data = wOp.read_as_byte(); uint8_t *dptr; newType = RankedTensorType::get({lshape[0], rshape[0], rshape[1], rshape[2]}, module::getElementType(rhs)); std::vector<float_t> new_filter(newType.getNumElements(), 0); dptr = (uint8_t *)new_filter.data(); // 实际的数据复制过程 for (int32_t i = 0; i < lshape[0]; i++) { auto offset = i * data->size(); memcpy(dptr + offset, data->data(), data->size()); } auto new_op = top::WeightOp::create(op, "folder", new_filter, newType); wOp.replaceAllUsesWith(new_op.getDefiningOp()); operands.push_back(new_op); rewriter.eraseOp(wOp); } else { // 对于普通tensor, 先reshape成[1, b, e, d] 再用tile算子翻倍数据为 [a, b, e, d] // Reshape操作 auto loc = NameLoc::get(rewriter.getStringAttr(rname + "_reshape")); newType = RankedTensorType::get({1, rshape[0], rshape[1], rshape[2]}, module::getElementType(rhs)); auto rrsop = rewriter.create<ReshapeOp>(loc, newType, ValueRange{rhs}); // Tile操作，各维tile倍数[a,1,1,1] newType = RankedTensorType::get({lshape[0], rshape[0], rshape[1], rshape[2]}, module::getElementType(rhs)); loc = NameLoc::get(rewriter.getStringAttr(rname + "_tile")); attrs.push_back(rewriter.getNamedAttr("tile", rewriter.getI64ArrayAttr({lshape[0], 1, 1, 1}))); auto tileOp = rewriter.create<TileOp>(loc, newType, ValueRange{rrsop}, attrs); attrs.clear(); operands.push_back(tileOp); } operands.push_back(none); // 这里使用了右操作数转置的批量矩阵乘法算子, 硬件可直接支持 // [a*b, c, d] * [a*b, e, d]^T -> [a*b, c, e] attrs.push_back(rewriter.getNamedAttr("right_transpose", rewriter.getBoolAttr(true))); rewriter.setInsertionPoint(op); auto matmulOp = rewriter.create<MatMulOp>(op.getLoc(), op.getType(), operands, attrs); op.replaceAllUsesWith(matmulOp.getOperation()); rewriter.eraseOp(op); } else if (mode == "abcd,ced->abce") { // dumb implementation // 转置lhs [a, b, c, d] -> [a, c, b, d] // trans_shape = [lhs_shape[0], lhs_shape[2], lhs_shape[1], lhs_shape[3]] rewriter.setInsertionPointAfter(lhs.getDefiningOp()); auto loc = NameLoc::get(rewriter.getStringAttr(lname + "_trans")); auto newType = RankedTensorType::get({lshape[0], lshape[2], lshape[1], lshape[3]}, module::getElementType(lhs)); attrs.push_back(rewriter.getNamedAttr("order", rewriter.getI64ArrayAttr({0, 2, 1, 3}))); auto tranOp = rewriter.create<PermuteOp>(loc, newType, ValueRange{lhs}, attrs); attrs.clear(); operands.push_back(tranOp); // 复制或Tile lhs: [c,e,d] -> [a,c,e,d] rewriter.setInsertionPointAfter(rhs.getDefiningOp()); if (auto wOp = dyn_cast<top::WeightOp>(rhs.getDefiningOp())) { // Weight翻倍数据 auto storage_type = module::getStorageType(rhs); assert(storage_type.isF32() && "Todo, supoort more weight type"); auto data = wOp.read_as_byte(); uint8_t *dptr; newType = RankedTensorType::get({lshape[0], rshape[0], rshape[1], rshape[2]}, module::getElementType(rhs)); std::vector<float_t> new_filter(newType.getNumElements(), 0); dptr = (uint8_t *)new_filter.data(); for (int32_t i = 0; i < lshape[0]; i++) { auto offset = i * data->size(); memcpy(dptr + offset, data->data(), data->size()); } auto new_op = top::WeightOp::create(op, "folder", new_filter, newType); wOp.replaceAllUsesWith(new_op.getDefiningOp()); operands.push_back(new_op); rewriter.eraseOp(wOp); } else { // rehshape + tile: [c,e,d] -reshape->[1,c,e,d]-tile->[a,c,e,d] loc = NameLoc::get(rewriter.getStringAttr(rname + "_reshape")); newType = RankedTensorType::get({1, rshape[0], rshape[1], rshape[2]}, module::getElementType(rhs)); auto rrsop = rewriter.create<ReshapeOp>(loc, newType, ValueRange{rhs}); loc = NameLoc::get(rewriter.getStringAttr(rname + "_tile")); attrs.push_back(rewriter.getNamedAttr("tile", rewriter.getI64ArrayAttr({lshape[0], 1, 1, 1}))); newType = RankedTensorType::get({lshape[0], rshape[0], rshape[1], rshape[2]}, module::getElementType(rhs)); auto tileOp = rewriter.create<TileOp>(loc, newType, ValueRange{rrsop}, attrs); attrs.clear(); operands.push_back(tileOp); } operands.push_back(none); // 右操作数带转置批量矩阵乘法：[a*c, b, d] * [a*c, e, d]^T -> [a*c, b, e]->[a, c, b, e] newType = RankedTensorType::get({lshape[0], lshape[2], lshape[1], rshape[1]}, module::getElementType(op)); attrs.push_back(rewriter.getNamedAttr("right_transpose", rewriter.getBoolAttr(true))); rewriter.setInsertionPoint(op); loc = NameLoc::get(rewriter.getStringAttr(name + "_matmul")); auto matmulOp = rewriter.create<MatMulOp>(loc, newType, operands, attrs); attrs.clear(); // [b, w, h, k] -> [b, h, w, k] attrs.push_back(rewriter.getNamedAttr("order", rewriter.getI64ArrayAttr({0, 2, 1, 3}))); auto tranBackOp = rewriter.create<PermuteOp>(op.getLoc(), op.getType(), ValueRange{matmulOp}, attrs); op.replaceAllUsesWith(tranBackOp.getOperation()); rewriter.eraseOp(op); } else if (mode == "abcd,abed->abce" || mode == "abcd,abde->abce") { // lhs(abcd) * rhs(abed)^T -> abce // lhs(abcd) * rhs(abde) -> abce auto newType = RankedTensorType::get({lshape[0], lshape[1], lshape[2], rshape[2]}, module::getElementType(op)); if (mode == "abcd,abde->abce"){ newType = RankedTensorType::get({lshape[0], lshape[1], lshape[2], rshape[3]}, module::getElementType(op)); } rewriter.setInsertionPoint(op); rewriter.setInsertionPointAfter(rhs.getDefiningOp()); operands.push_back(lhs); operands.push_back(rhs); operands.push_back(none); if (mode == "abcd,abed->abce"){ //rhs(abed)^T attrs.push_back(rewriter.getNamedAttr("right_transpose", rewriter.getBoolAttr(true))); } auto loc = NameLoc::get(rewriter.getStringAttr(name)); auto matmulOp = rewriter.create<MatMulOp>(loc, newType, operands, attrs); op.replaceAllUsesWith(matmulOp.getOperation()); attrs.clear(); rewriter.eraseOp(op); } else if (mode == "abcd,cde->abce"){ // lhs : // abcd -> acbd(pemute) // rhs : // cde -> 1cde(reshape) // acde -> acde(tile) // matmul: // lhs(acbd) * rhs(acde) = result(acbe) // result: // acbe -> abce(pemute) // success! rewriter.setInsertionPointAfter(lhs.getDefiningOp()); auto loc = NameLoc::get(rewriter.getStringAttr(lname + "_trans")); auto newType = RankedTensorType::get({lshape[0], lshape[2], lshape[1], lshape[3]}, module::getElementType(lhs)); attrs.push_back(rewriter.getNamedAttr("order", rewriter.getI64ArrayAttr({0, 2, 1, 3}))); auto tranOp = rewriter.create<PermuteOp>(loc, newType, ValueRange{lhs}, attrs); attrs.clear(); operands.push_back(tranOp); rewriter.setInsertionPointAfter(rhs.getDefiningOp()); if (auto wOp = dyn_cast<top::WeightOp>(rhs.getDefiningOp())) { auto data = wOp.read_as_byte(); uint8_t *dptr; newType = RankedTensorType::get({lshape[0], rshape[0], rshape[1], rshape[2]}, module::getElementType(rhs)); std::vector<float_t> new_filter(newType.getNumElements(), 0); dptr = (uint8_t *)new_filter.data(); for (int32_t i = 0; i < lshape[0]; i++) { auto offset = i * data->size(); memcpy(dptr + offset, data->data(), data->size()); } auto new_op = top::WeightOp::create(op, "folder", new_filter, newType); wOp.replaceAllUsesWith(new_op.getDefiningOp()); operands.push_back(new_op); rewriter.eraseOp(wOp); } else { loc = NameLoc::get(rewriter.getStringAttr(rname + "_reshape")); newType = RankedTensorType::get({1, rshape[0], rshape[1], rshape[2]}, module::getElementType(rhs)); auto rrsop = rewriter.create<ReshapeOp>(loc, newType, ValueRange{rhs}); loc = NameLoc::get(rewriter.getStringAttr(rname + "_tile")); attrs.push_back(rewriter.getNamedAttr("tile", rewriter.getI64ArrayAttr({lshape[0], 1, 1, 1}))); newType = RankedTensorType::get({lshape[0], rshape[0], rshape[1], rshape[2]}, module::getElementType(rhs)); auto tileOp = rewriter.create<TileOp>(loc, newType, ValueRange{rrsop}, attrs); attrs.clear(); operands.push_back(tileOp); } operands.push_back(none); newType = RankedTensorType::get({lshape[0], lshape[2], lshape[1], rshape[2]}, module::getElementType(op)); rewriter.setInsertionPoint(op); loc = NameLoc::get(rewriter.getStringAttr(name + "_matmul")); auto matmulOp = rewriter.create<MatMulOp>(loc, newType, operands, attrs); attrs.clear(); attrs.push_back(rewriter.getNamedAttr("order", rewriter.getI64ArrayAttr({0, 2, 1, 3}))); auto tranBackOp = rewriter.create<PermuteOp>(op.getLoc(), op.getType(), ValueRange{matmulOp}, attrs); op.replaceAllUsesWith(tranBackOp.getOperation()); rewriter.eraseOp(op); } else { llvm_unreachable("Einsum not support this mode now"); } return success(); }

总结

TPU-MLIR对EinSum的实现虽然不完全，但已经足够实用，能满足目前常见网络的需求。通过Converter直接表达式规范化，降低了编译器优化或模式分析的复杂性。在算子分析时，我们不仅需要在计算上实现等价变换，还需充分了解实际硬件的特性。针对不同硬件架构及其对算子的支持情况，需具体分析以找到最佳实现方法。此外，我们可以看到在工程实践中，人们更注重实用性和效率，在实现上不必追求完备，是要覆盖实际应用场景即可。EinSum的转换还有改进空间，我们也欢迎社区提出宝贵的建议并贡献代码。