那么在太阳的引力下,为什么月球不脱离地球的引力独立运转呢?
地球对月球的引力是2.5倍的原因又是什么呢?
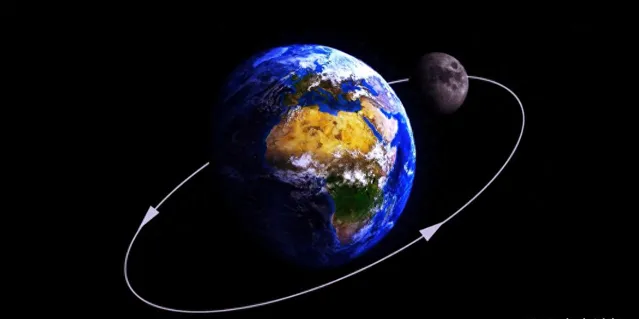
其实月球不脱离地球引力独立运转是有原因的,下面我们就来一探二者引力大小的奥秘!
作为行星家族的一员,地球与月球的运行状态由太阳的引力所决定。
太阳作为太阳系的中心,拥有恒定的引力,位于行星家族的中心位置,如同巨大的吸盘吸引着行星家族的所有行星向自己靠拢。

那么在太阳的引力作用下,它会对地球和月球产生什么样的影响呢?
在太阳的作用下,地球免不了会受到太阳的引力影响,但不同时间受到的引力大小也是不同的。
这是因为地球在轨道上不是固定不动的,处于不断运动的状态,同时按照开普勒三定律,行星与它的中心之间的吸引力与行星与中心之间的距离平方成反比。

地球在绕太阳运动的过程中,驶离太阳的距离也会有所增加, 所以此时地球受到太阳的引力并不是很强。
而地球在轨道上它的速度是非常快的,随着太阳的引力加速的驶向太阳,到了最近距离的时候,地球将会受到最大的引力。
而此时地球的速度已经非常快了,它的向心力也非常大,如果地心力没有受到太阳引力的物理作用,地球就会直接飞出太阳的引力范围,但是地心力受到太阳的引力的约束,所以地球就会绕太阳做圆周运动。

太阳的引力对地球来说是非常的重要,那么对于月球呢?
由于在太阳系中,月球比较特殊,它就跟随着地球一同绕太阳运动。
在太阳的引力作用下,月球不仅受到地球的引力约束,还需要克服太阳对它的引力,而且太阳对月球的引力是地球对月球引力的2.5倍,所以月球绕地球运转是一件自然而然的事情。
那么地球对月球的引力为什么是2.5倍呢?
要解答这个问题就需要从行星的引力公式来进行推导!

引力公式是由牛顿提出的,他通过实验和数学模型的数学表达式得出了引力公式:
F=GM1M2/r^2;
式中:G是万有引力常数,值为6.67*10^-11 N·m^2/kg^2,是一个恒定数值;
M1是第一个物体的质量;
M2是第二个物体的质量;
r是两个物体之间的距离;
F是两个物体之间的作用力。

根据引力公式,我们可以得出:
引力大小与两者之间质量的和成正比;
引力大小与两者之间的距离平方成反比。
根据上述公式,我们可以得出太阳对地球的引力大小与太阳对地球的引力大小有所不同。

太阳对地球的引力大小:FD=GM太阳M地球/r^2;
而如果计算太阳对地球的引力大小的时候:
太阳的质量:1.9910^30kg;
地球的质量:5.9810^24kg;
太阳和地球之间的距离是1.4910^11m;
将这些数据带入引力公式中进行计算,可得出:FD=3.5310^22N。
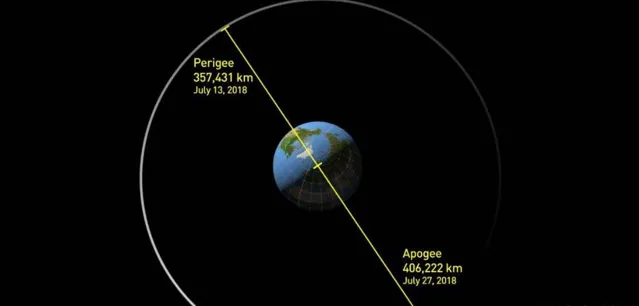
太阳对月球的引力大小:FM=GM太阳M月球/r^2;
太阳的质量:1.9910^30kg;
月球的质量:7.3510^22kg;
太阳和月球之间的距离是1.4910^11m;
将这些数据带入引力公式中进行计算,可得出:FM=1.9810^20N。
M是月球的质量,所以地球对月球的引力:F=GM1M2/r^2;
地球对月球的引力:FED=GM月球M地球/r^2;

将M1和M2互换位置,可得:
FDE=GM地球M月球/r^2;
M地球:M太阳=1:333000;
M太阳=G
M月球;
FDE=FED+FM;
FDE=2.5FM;
FDE=2.51.9810^20N;
FDE=4.9510^20N。
所以地球对月球的引力为4.95*10^20N。
地球对月球的引力是2.5倍,而太阳对月球的引力是地球对月球引力的2.5倍,那么根据以上的推导,月球是绕地球还是绕太阳运转。

根据开普勒定律可知,太阳对行星的引力会让其绕太阳运转,而地球对月球的引力是太阳对月球的引力2.5倍,又因为地球在运行过程中不断变速。
M太阳对地球的引力平方和地球对月球的引力平方之间的大小关系为:
GM太阳M地球/1A^2=2.5GM太阳M月球/B^2;
M太阳,G,1均为恒定数值,所以可以进行约分,整理得出:
A^2=2.5B^2;
A=√2.5B。
太阳对地球的引力是地球对月球的2000倍,地球对月球的引力是太阳对月球的2.5倍。
所以月球是绕地球运转的,所以月球不会脱离地球引力而独立运转。











