
开启愉快的旅程
生活中,我们会遇到很多不断「连续变化的量」,例如我们开车上路时,汽车的里程是在连续不断变化着的,里程表上的公里数值一直在上升。虽然某一时刻都对应着一个具体的里程值,但这个里程值并不是孤立存在的,它有变化能力,这个变化能力具体是多大呢?

里程在上升,上升得有多快呢?
我们可以看下速度表,某一时刻速度表上的数字,就是该时刻里程的变化能力,这个变化能力我们也称之为「变化率」,例如一小时能上升30公里的里程。

速度就是里程变化快慢的度量,即里程的变化率
数学的角度,怎么计算出这个变化率呢?如果汽车是直线匀速行驶的,我们只需用小学的除法,就可以简单计算出来:总里程÷行驶所用时间=速度,速度就是某时刻里程上升快慢能力的具体数值。

匀速运动,用普通除法就能算出变化率
现实中车辆的速度,是时快时慢的,要求出某个时刻的对应速度,普通除法搞不定(普通除法只能得到速度的平均值),这时就需要用到更高一级的特殊除法:导数。导数是把除法加入极限思维后的一种计算方法,目的就是用来求出变化率。
还是以汽车的里程变化快慢为例,总里程÷行驶所用时间=平均速度,这个比值关系式里,如果「行驶所用的时间」无限接近零,那么所求出的比值,就无限接近该时刻的真实速度值,也就是计算出这个比值在分母部分趋于零时,无限接近的那个数值,就得了速度。这种计算比值极限的方法,就是导数。
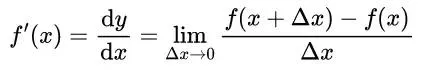
导数的定义
求出汽车里程的导数,就得到了速度。
那里程的微分,又是什么呢?用某时刻对应的速度,乘以一段时间的改变量,就是该时刻里程的微分,例如在行驶到0.5小时的时候,假设此时对应的速度为56公里每小时,则此时刻对应的里程微分表达式,就是:此时刻路程的微分=56×时间改变量,时间改变量的值可以任意取,例如取0.3小时,具体的微分值就是56×0.3=16.8,注意汽车继续行驶了0.3小时后,实际的里程并不一定是16.8公里,因为速度是变化的,而不是一直保持在56公里每小时不变,所以某时刻里程的微分,就是以该时刻的速度为基础,所计算出来里程变化量的近似值,这个近似值与真实值显然存在着误差,当时间改变量的取值无限接近接近零时,这个误差也将无限接近零,而且它接近零的程度,比时间改变量自己接近零的程度还厉害,数学上称为「更高阶」。从函数图像上看,某时刻里程的微分,就是里程函数的曲线,在该时刻的切线的上升高度。
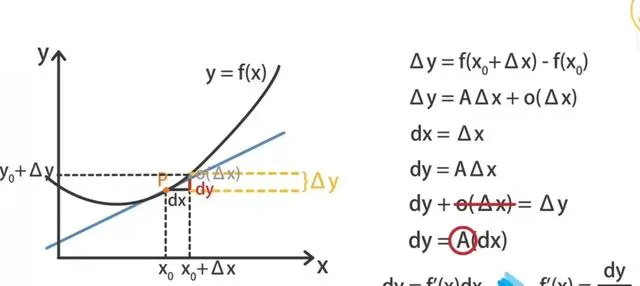
函数曲线上某点对应于自变量改变量的微分,就是该点切线的变化高度dy,它是曲线实际变化高度△y的近似值
利用里程的变化率,也就是速度,得出微分表达式后,就可以反过来可以求出实际的里程,方法就是「积分」运算 ,也就是变化率的逆运算——求出原函数,类似于乘除法互为逆运算,其实乘除法可以看成是微积分运算的特殊情况,即在变化率固定不变时的运用。

数学 ,就是这么有趣。











