
在本质上,有两种方法可以证明中心极限定理。第一种是经验性的,而第二种则使用数学思维的完美精确性。本文将介绍这两种方法。
在实际应用的经验方法中,你可以直观地观察中心极限定理(CLT)的效果,看到它在实验中如何发挥作用,或者在某些情况下可能完全不起作用。这种方法主要是在特定的数据集上检验中心极限定理的有效性,而不是通过理论推导来证明其正确性。
我将进行这个实验,使用真实的、物理的对象——那些你可以用手指捡起来,拿在眼前,甚至放进嘴里的物体。我还将测试这个实验的结果是否正态分布。
理论方法是一个完整的数学证明,通过以下五个概念层层推进:
- 泰勒定理(由此引出泰勒级数)
- 矩生成函数
- 泰勒级数
- 生成函数
- 无限序列和级数
支撑这庞大概念结构的是广阔而繁茂的微积分领域。
我将解释这五个概念,并展示每一个概念是如何在下面一个的基础上构建,直至它们全部联合起来证明了这个统计科学中最深远且令人愉快的定理之一。
中心极限定理
简而言之,中心极限定理提出了以下强有力的声明:
标准化样本均值在分布上收敛于标准正态随机变量。
这个定义由四个术语构成:
标准化(standardized ) ,意味着从随机变量中减去其均值,从而将整个样本沿X轴滑动到均值为零的点,然后将这个平移的样本除以其标准差,从而仅用标准差的分数数值表达每个数据点的值。
样本均值(sample mean ) ,简单来说就是你的随机样本的均值。
在分布上收敛(converges in distribution ) ,意味着当你的样本增大到无限大时,你在样本上定义的随机变量(在我们的案例中,是样本均值)的累积概率函数(CDF)越来越像其他一些特定的随机变量的CDF(在我们的案例中,另一个变量是标准正态随机变量)。这就引出了,
标准正态随机变量(standard normal random variable ) ,这是一个均值为零且方差为1的随机变量,且呈正态分布。
中心极限定理的非正式表述可以是:
对于大样本量,样本均值或多或少围绕真实的总体均值呈正态分布。
现在,我们将称量一些糖果。我买了两包Nerds糖果,目的是测量一个Nerds糖果的平均重量。

对我来说,Nerds的总体数量显然是无法知道的,总体的平均重量也是如此。我的目标是知道一个Nerds的平均重量,这个目标有可能无法实现。
大自然不会轻易揭示的,我们必须推断。因此,我将两盒的糖果混合在一起,随机挑选了30个Nerds(葡萄味和草莓味各15个),称量了这个样本,计算了其平均值,然后将样本放回堆中。

我重复了这个过程50次,得到了50个不同的样本均值:
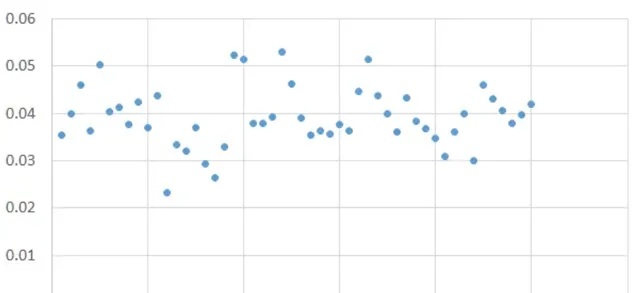
接下来,我使用以下公式标准化了这50个样本均值:

标准化样本均值
这里,0.039167是50个样本均值的均值,而0.006355是它们的标准差。
50个标准化均值的频率分布图显示了以下分布形态:

标准化样本均值的频率分布
样本均值看起来整齐地围绕着未知的(且永远无法知道的)总体均值排列,看起来像是一个正态分布。 但这个分布真的是正态的吗?我怎么能确定它在更大的样本量或更多的样本中不会变成以下形状呢?
在19世纪早期 ,当皮埃尔-西蒙·拉普拉斯在发展他的中心极限定理的想法时,他评估了许多这样的分布形状。事实上,上面显示的形状是他的最爱之一。另一个强有力的竞争者是他的同胞亚伯拉罕·德·莫弗尔发现的正态曲线。那时候,正态分布还没有现在的名字。也没有发现它的广泛适用性。无论如何,它绝对没有像今天这样受到高度的重视。
为了知道我的数据是否真的是正态分布,我需要的是一个 正态性统计检验(statistical test of normality ) ——一个检验,会检查数据是否遵循正态曲线的分布属性。这种检验的结果通常会给出一个p值,这个p值可以转化成一个置信度百分比(,表明数据分布与正态分布的吻合程度。
幸运的是,我的需求(检验是否为正态分布)不仅是一个普遍的需求,而且还是一个研究得非常深入的需求。在过去的100年中,科学家们至少发明了十种不同的正态性检验。1980年,两位先生卡洛斯·哈尔克和阿尼尔·K·贝拉发明了其中一种测试。它基于一个极其简单的观察。如果数据是正态分布的,那么其偏度(S)将为零,峰度(K)将为3(我将在后面解释这些是什么)。使用S、K和样本量n,哈尔克和贝拉先生构建了一个特殊的随机变量,称为JB:

JB是检验统计量。研究人员证明,如果你的数据来自正态分布的总体,那么JB将呈 卡方分布( Chi-squared distributed ) ,自由度为2。这个检验的零假设是你的数据是正态分布的。 检验统计量的p值是你的数据来自正态分布总体的概率。他们的检验被称为Jarque-Bera正态性检验。
当我对50个样本均值的集合进行JB检验时,检验结果表明,否定检验的零假设将是不明智的。检验统计量为jb(50) = 0.30569,p = .86。
下面是我进行的经验方法的总结:
- 我抽取了50个随机样本(有放回),每个样本大小为30。
- 我计算了每个样本的样本均值X_bar_i。
- 我标准化了每个样本均值得到Z_bar_i。
- 我对50个标准化样本均值进行了JB正态性检验,以测试它们是否呈正态分布。
中心极限定理的数学证明
有两种方法可以数学上证明CLT。第一种方法使用 特征函数( Characteristic Functions ) 的属性。第二种方法使用 矩生成函数 (MGF)的属性。特征函数和矩生成函数是生成函数的不同形式。基于CF的证明比基于MGF的证明假设更少。通常来说,它也是一个坚实的、独立的证明。但我不会使用它,因为比起CF,我更喜欢MGF。
回到基于MGF的证明,如果你了解以下四个概念,你将能够最大限度地欣赏它:
- 序列和级数
- 泰勒级数
- 生成函数
- 矩生成函数
我将从解释这些概念开始。如果你已经知道它们是什么,你可以直接跳到证明部分。
序列
序列只是按某种顺序排列的东西。在序列中,顺序非常重要。事实上,顺序就是一切。
在数学中,一个包含(n+1)个元素的序列如下写出:
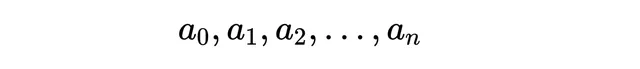
级数
取任何一个序列。现在将其元素之间的逗号换成加号。你得到的就是一个级数:
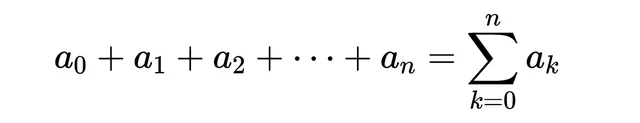
级数是有限的或无限的,取决于其中的项数。无论哪种方式,如果它的总和是一个有限的值,它就是一个收敛级数。否则,它是一个发散级数。
这里有一些例子。


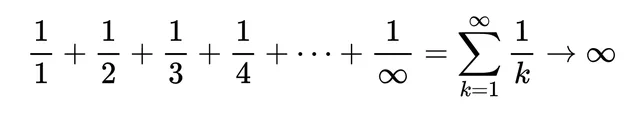
如果你不是将序列的所有元素相加,而是将它们相乘,得到的就是一个乘积级数。也许最著名的无限收敛乘积级数的例子是下面这个:
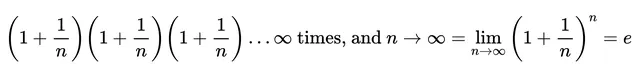
雅各布·伯努利基于e的乘积级数公式
无限级数是生成函数的基础,这将是我接下来讨论的主题。
生成函数
理解生成函数的诀窍在于欣赏 标签制造机 的实用性。
想象一下,你的工作是给新建的图书馆、仓库、储藏室等需要大量使用标签的地方贴标签。你刚接到一个任务,去给一个全新的仓库贴标签。仓库的通道从1到26号,每个通道(从前到后)有50个存储位置或单元,每个通道的垂直高度被划分为5个存储层级,每层都设有架子用于放置物品。
你可以像这样打印出6500个标签:
A.1.1,A.1.2, …, A.1.5,A.2.1, …, A.2.5, …,A50.1, …, A50.5,
B1.1, …, B2.1, …, B50.5, … 一直到Z.50.5,
这里有一个提高效率的建议:你可以考虑将需要的标签序列提前编程到标签机中。这样做的话,你只需携带这台标签机前往目的地。到了仓库后,装上一卷用于打印的胶带。在仓库中,你可以简单地按下机器上的按钮,预设的「A」通道的所有标签就会自动打印出来。
标签机就是这个以及其他类似序列的生成函数:
A.1.1, A.1.2, …, A.1.5, A.2.1,…,A.2.5, …,A50.1,…,A50.5
在数学中,生成函数是一种你设计用来生成你选择的序列的数学函数,这样你就不必记住整个序列。
一个非常简单的生成函数如下图所示,对应以下无限序列:1, 1, 1, 1, 1, …:

1的无限序列的生成函数
如你所见,一个生成序列实际上是一个级数。
一个稍微复杂一点的生成序列,也是一个著名的生成序列,是生成(n+1)个二项式系数序列的序列:
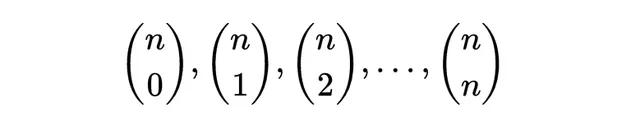
二项式系数序列
每个系数nCk给出了从n个对象中选择k个的不同方式的数量。这个序列的生成函数是(1 + x)的n次幂的二项式展开:

n+1二项式系数序列的生成函数
在这两个例子中,x项的系数构成了序列。不同幂次的x项主要用来将系数彼此分开。如果没有x项,求和就会将所有系数融合成一个单一的数字。
我向你展示的两个生成函数示例说明了普通生成函数(OGF)的应用,它有以下一般形式:
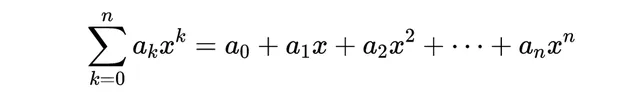
普通生成函数
另一个非常有用的形式是指数生成函数(EGF):
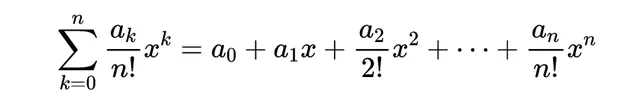
指数生成函数
之所以称为指数生成函数,是因为分母中阶乘项的值以指数速度增长,导致连续项的值以指数速度减小。
EGF有一个非常有用的特性:其第k次导数,在x=0处求值时,可以单独得到序列中的第k个元素a_k。下面是如何通过对上述EGF求第三次导数并在x=0处评估得到系数a_3的示例。所有其他项都消失:
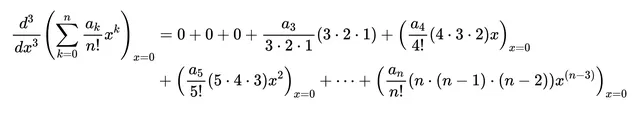
下一个话题
泰勒级数
泰勒级数是一种使用无限级数来近似函数的方法。函数f(x)的泰勒级数展开如下所示:
在计算前两项时,我们使用了0! = 1! = 1的事实。
f⁰(a), f¹(a),f²(a),等是在x=a处求得的f(x)的第0阶、第1阶、第2阶等导数。f⁰(a)简单来说就是f(a)。只要函数在x = a处可以无限次微分,即在x = a处存在所有从1到无穷的k阶导数,那么a可以是任何值。
尽管泰勒级数的发现具有革命性意义,但它并不总是表现良好。它为像1/x或1/(1-x)这样的函数创建了质量较差的近似,这些函数在其定义域的某些点,如x = 0和x = 1处趋于无穷大。这些函数中存在奇点。泰勒级数在描述快速波动的函数时也有困难。还有一些函数的基于泰勒级数的展开收敛速度非常慢。
泰勒级数是最常用的数学工具之一,如证明中心极限定理,你会发现将泰勒级数分成两部分很有用,如下所示:

这里,从索引'r'分割了级数。我们将两部分称为T_r(x)和R_r(x):

T_r(x)被称为在x=a处求值的r阶泰勒多项式。
R_r(x)是使用r阶泰勒多项式在x=a处近似f(x)得到的余数或剩余部分。
我们将 泰勒定理(Taylor’s theorem) 来证明中心极限定理,这是泰勒级数合法性的来源。 泰勒定理指出,随着 x → a,剩余项 R_r(x) 比多项式 (x - a) 的 r 次幂收敛到 0 的速度更快。 泰勒定理的陈述可以形式化为以下等式:

泰勒级数的众多用途之一在于为随机变量的矩创建生成函数。这就是我们接下来要做的。
矩和矩生成函数
随机变量 X 的第 k 阶矩是 X 的 k 次幂的期望值。

这被称为第 k 阶原始矩。
X 关于某个值 c 的第 k 阶矩被称为 X 的第 k 阶中心矩。它只是 (X - c) 的第 k 阶原始矩:
X 的第 k 阶标准化矩是 X 的第 k 阶中心矩除以 X 的标准差的 k 次幂:
X 的前 5 个矩具有以下特定的值或含义:
第四矩之后,解释变得相当模糊。
有这么多矩,如果拥有一个可以生成它们的函数岂不是很棒?这就是矩生成函数(MGF)的用途。泰勒级数使得创建 MGF 变得非常容易。让我们看看如何创建它。
我们定义一个新的随机变量tX其中t是实数。这是e ^ tX在t = 0时的泰勒级数展开式:
在上述等式的两侧应用期望运算符:
通过期望的线性(和缩放)规则:E(aX + bY) = aE(X) + bE(Y),我们可以如下将期望运算符移入求和内:
回想一下,E(X^k) 是 k = 0,1,2,3,… 的 X 的原始矩。
让我们将等式(2)与指数生成函数的一般形式进行比较:
我们观察到什么?我们看到等式 (2) 中的 E(X^k) 是 EGF 中的系数 a_k。因此,等式 (2) 是 X 矩的生成函数,因此 X 的矩生成函数的公式如下:
MGF 有许多有趣的特性。我们将在中心极限定理的证明中使用其中的一些。
还记得EGF的第k阶导数在x = 0处的取值是如何给出底层序列的第k个系数的吗?我们将利用EGF的这个性质从它的MGF中提取X的矩。
X在t=0时的MGF的零阶导数可以通过简单地将t=0代入方程(3)中得到。M⁰_X(t=0)的值为1。X在t=0处的MGF的一、二、三阶导数分别表示为M¹_X(t=0)、M²_X(t=0)、M³_X(t=0)。分别求出X的第一、第二、第三阶原始矩,如下图所示:
这给了我们MGF的第一个有趣和有用的性质。 MGF在t = 0处的k阶导数是X的第k个原始矩。
在接下来的证明中,我们会发现MGF的第二个性质是:如果两个随机变量X和Y具有相同的矩生成函数,那么X和Y具有相同的累积分布函数:
如果X和Y具有相同的MGF,这意味着它们的均值、方差、偏度、峰度以及所有更高阶矩(无论这些矩可能代表什么人类无法理解的现实方面)都完全相同。如果X和Y的CDF的每一个性质相应地相同,你会期望它们的CDF也相同。
我们将使用的MGF的第三个性质适用于X,当X被a放大并且由b平移时:
我们将使用的MGF的第四个性质适用于‘n’个独立同分布的随机变量之和的MGF:
在我们证明CLT之前,最后的结果是标准正态随机变量N(0,1)的MGF,如下所示:
说到标准正态随机变量,如等式(4)所示,N(0,1)的MGF的一、二、三、四阶导数在t = 0处求值时,第一阶矩(均值)为0,第二阶矩(方差)为1,第三阶矩(偏态)为0,第四阶矩(峰度)为1。
有了这些,我们需要的证明CLT的机制已经就位。
中心极限定理的证明
设X_1, X_2,…,X_n为'n'个独立的随机变量,形成大小为'n'的随机样本。假设我们从一个均值为μ,方差为σ²的总体中抽取了这个样本。
设X_bar_n是样本均值:
设Z_bar_n是标准化的样本均值:
中心极限定理指出,当' n '趋于无穷时,Z_bar_n在分布上收敛于n(0,1),即Z_bar_n的CDF与n(0,1)的CDF相同,n(0,1)通常用希腊字母φ (phi)表示:
为了证明这一点,我们将使用MGF的性质(式5),即如果X和Y的MGF相同,那么它们的CDF也相同。在这里,只需证明随着n趋于无穷大,Z_bar_n的MGF收敛到N(0, 1)的MGF,正如我们所知(式8),这是e的t²/2次幂。简而言之,我们希望证明以下等式:
让我们定义一个随机变量Z_k如下:
现在我们用Z_k来表示标准化均值Z_bar_n,如下所示:
接下来,在式(9)的两边应用MGF运算符:
通过构造,Z_1/√n,Z_2/√n, …, Z_n/√n是独立的随机变量。因此我们可以使用MGF的性质(7a),它表达了n个独立随机变量之和的MGF:
根据定义,Z_1/√n, Z_2/√n, …, Z_n/√n也是相同的随机变量。因此我们可以假设如下:
Z_1/√n = Z_2/√n = … = Z_n/√n = Z/√n.
因此使用性质(7b)我们得到:
最后,我们还将使用性质(6)来表达一个随机变量的MGF(在这种情况下,Z)被一个常数(在这种情况下,1/√n)缩放时如下:
通过这一步,我们将寻找Z_bar_n的矩生成函数(MGF)的目标转变为寻找Z/√n的MGF。
M_Z(t/√n)是一个普通函数,接受(t/√n)作为参数。因此,我们可以在t = 0处为M_Z(t/√n)创建一个泰勒级数展开,如下所示:
接下来,我们将这个展开分为两部分。第一部分是一个有三个项的有限级数,对应于k = 0, k = 1和k = 2。第二部分是无限级数的剩余部分:
在上述级数中,M⁰、M¹、M²等是矩生成函数M_Z(t/√n)在(t/√n) = 0处的第0次、第1次、第2次导数。我们已经知道MGF的这些导数恰好是Z的0阶1阶2阶等等。
0阶矩,M⁰(0),始终为1。回忆一下,根据其构造,Z是一个标准正态随机变量。因此,它的第一矩(均值),M¹(0),是0,它的第二矩(方差),M²(0),是1。有了这些值,我们可以如下表达上述泰勒级数展开:
M_Z的上述展开式的另一种表达方式是2阶泰勒多项式的和,它捕获展开式的前三个项,以及捕获求和的剩余项:
我们已经求过o(2)泰勒多项式的值。所以我们找到Z的MGF的任务现在进一步简化为计算余数项R_2。
在着手计算R_2之前,让我们退后一步,回顾一下要证明的内容。我们希望证明,随着样本大小‘n’趋于无穷大,标准化的样本均值Z_bar_n在分布上收敛于标准正态随机变量N(0, 1):
为了证明这一点,我们意识到当N趋于无穷时,Z_bar_n的MGF收敛于N(0,1)的MGF就足够了。
这使我们开始寻找Z_bar_n的MGF,首先在等式(10)中展示:
但真正的问题是,我们不仅希望计算这个MGF的极限,随着n趋于无穷大,还要让它等于e的t²/2次幂。
为了实现这一目标,我们将通过依次应用式(12)和式(11)来解包和简化式(10)的内容,如下所示:
在我们的证明中,这里有一个不舒服的地方 。看看上面最后一行的等式。你不能只是将极限强加到右侧的大括号内并将黄色项归零。这样盲目操作的问题在于,大括号的指数中有一个‘n’,这正是想要无限增大的n。但现在注意这一点:我说你不能将极限强加到大括号里,但我从未说你不能偷偷地引入它。
所以我们要狡猾一点。我们会证明,当n趋于无穷时,余项R_2(用黄色标出)独立地收敛于零不管它的指数是多少。如果我们在这方面取得了成功,常识推理表明,将其从 等式的右侧中消灭是「合法的」,无论是否有指数。
为了证明这一点,我们将使用我在等式(1)中引入的泰勒定理:
把这个定理应用到我们的研究中,设x = (t/√n) r = 2,如下所示:
接下来,我们将a设为0,这允许我们立即切换极限:
(t/√n) → 0, 到,
n → ∞, 如下:
现在我们做一个重要但不完全明显的观察。在上述极限中,注意到只要n趋于无穷大,左边将趋于零,不管t的值是多少,只要它是有限的。换句话说,左边将对任何有限的t值趋于零,因为极限行为完全由分母中的(√n)²驱动。有了这个启示,我们有了将t²从分母中去掉而不改变左边式子极限行为的自由。同时我们还将(√n)²转移到分子,如下:
让这个结果在你的脑海中停留几秒钟,因为你很快就会需要它。与此同时,让我们回到随着n趋于无穷大的Z_bar_n的MGF的极限。我们将在简化这个极限的右侧方面取得更多进展,然后将其塑造成一个特定的形状:
看起来可能不像,但通过式(14),我们实际上距离证明中心极限定理只有两步之遥。
这一切都要归功于雅各布·伯努利对「e」的乘积级数公式的突破性发现。
我们将使用式(13)来消除式(14)中的一些项:
接下来我们将使用以下无限乘积级数表示e的x次幂:
在上述方程中,设x = t²/2并将这个结果代入式(15)的右侧,你就证明了中心极限定理:
随着样本大小趋于无穷大,标准化样本均值的MGF等同于标准正态随机变量的MGF。











