如何数出「无穷大」？

2024-01-08科学

作者 | [美]乔治·伽莫夫

翻译 | 吴先先

来源 | 节选自【数学知道一切的答案：从一到无穷大】，民主与建设出版社，2021年6月。

上一节中我们讨论了数字，其中有不少都是相当大的数。不过，即便是大到不可思议，就像西萨·班·达依尔要求的麦粒数目那么大，这些数字仍然是有限的。只要给足时间，人们就可以把这些数字从头到尾写下来。

不过，还有一些具有无穷性的数，无论花多少时间都写不完。例如，「所有整数的数量」显然是无穷大的，「一条线上所有几何点的个数」亦是如此。对于这样的数，我们除了说它们是无穷大的以外，还可以尝试其他的描述吗？换句话说，有没有可能比较两个不同的无穷数，看看哪一个「更大」？

「所有整数的个数和一条线上所有几何点的个数相比，哪一个更大」——这样的问题有意义吗？著名的数学家格奥尔格·康托尔（Georg Cantor）最先考察了这个乍看上去有点天马行空的问题，他是「无穷数学」当之无愧的开创者。

想要谈论无穷数的大小，就会有一个问题随之而来：我们既没法表示这些数字，也无法把它们写下来。这就有点儿像一个正在清点自己百宝箱的霍屯督人，他想知道自己手里的玻璃珠子多，还是铜币更多。相信你还记得，霍屯督人无法数出 3 以上的数字，那么，他会不会因为数不出珠子和铜币各自的数量，就放弃比较这两个数的大小呢？不一定。如果他足够聪明，就会把珠子和铜币逐一比较直至得出答案：把一颗珠子摆在一枚铜币边上，另一颗珠子摆在另一枚铜币边上，就这样摆下去。如果珠子用完了，铜币还剩下几枚，他就会知道，铜币比珠子更多；如果铜币用完了，还有几颗珠子，那么就是珠子比铜币多；如果两者同时用完，那就是一样多。

康托尔在比较无穷数时，用的也是完全相同的办法：把两组无穷数进行配对，如果这两个集合里的每一个元素都能一一对应，最后没有任何元素剩下，那么这两组无穷数就是相等的；如果其中一个集合里的有元素无法配对，那么就可以说，这组无穷数要比另一组更大一些，或者说更强一些。

这个方法无疑是可行的，事实上，要比较无穷大的数字，也只有这个法子了。不过，在真正开始采用这个方法之前，我们得做好大吃一惊的心理准备。比如说，我们来比较一下所有的奇数和偶数这两个无穷数集合。从直觉上判断，你肯定会觉得奇数和偶数一样多，而且它们也完全符合上述的规则，二者可以做到一一对应：

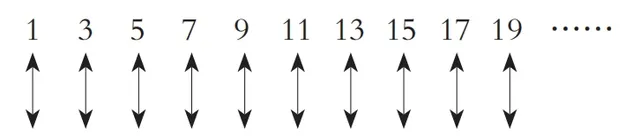
在这个表里，每一个奇数都对应着一个偶数，反之亦然。因此，奇数和偶数是大小相等的无穷数。看上去很简单，也很自然！

不过，稍等一下。下面这两个数，你觉得哪个更大：所有整数的数量（包括所有的奇数和偶数），还是所有偶数的数量？你当然会选择前者，因为它既包括了全部的偶数，也包括了全部的奇数。但这只是你的直觉而已。想要得到准确的答案，就必须应用无穷数比较的规则。如果你真的这么做了，就会吃惊地发现自己的直觉是错的。实际上，所有的整数和所有的偶数也可以放在如下这个表中，实现一一对应：

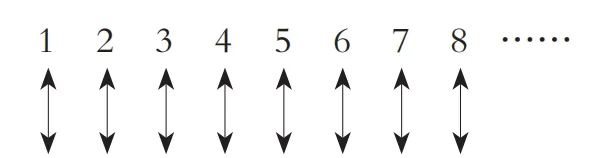
依照无穷数比较的规则，我们只能得出如下结论： 所有的偶数和所有的整数 个数完全相等。 当然，这听起来有点自相矛盾，因为偶数只是整数的一部分，但是必须要记住，我们在这里计算的是无穷数，它们的性质会不太一样。

没错， 在无穷数的世界里，部分确实有可能等于整体！ 最好的一个例证，莫过于德国数学家大卫·希尔伯特（David Hilbert）讲的一个故事。他在课堂上的这段话描述了无穷数的矛盾属性 ^[1] ：

「我们来想象一个旅馆，它的房间数量是有限的，而且所有房间都住满了人。假如有一个新客要求入住，那么老板会说：‘抱歉，所有房间都住满了。’再来想象另一家旅馆，这里有无穷个房间，同样，每一个房间里都住上了人。这时又有新客来访，要求入住。

「‘没问题！’旅馆老板会立刻答应下来，并把之前住在一号房的客人移到二号房，二号房的客人移到三号房，三号房的客人移到四号房，依此类推……这样，新客就可以住进调整后空置出来的一号房里了。

「我们再换个方式，想象一个同样有无穷多个房间的旅馆。所有的房间都客满，并且有无穷多个新客要求入住。

「‘好的，先生们，请稍等。’旅馆老板说道。

「紧接着，老板把一号房的客人移到二号房，二号房的客人移到四号房，三号房的客人移到六号房……以此调整。

「现在，所有门牌号是奇数的房间全都空置了，无穷多个新客人就可以轻松入住进去了。」

希尔伯特描述的这个场景可能不太容易想象，毕竟现在不是战时的华盛顿，没有那么多要住店的客人。不过这个例子很好地说明了在进行无穷数的运算时，我们会遇到一些和普通算术不太一样的运算属性。

依据康托尔的无穷数比较规则，我们还可以证明，所有分数（如 ,

）和所有整数的个数是相等的。我们可以按照如下的规则，把所有分数排成一排：先写出分子和分母之和等于 2 的分数，这样的分数只有一个，即；再写出分子和分母之和等于 3 的分数，即和；接下来是分子和分母加起来等于 4 的分数，包括和、和 ……，以此类推。按照这个步骤，我们会得到一个包含了所有分数的无限数列（图 5）。现在，在这个数列旁边写出整数的数列，就可以实现无穷多个分数和无穷多个整数的一一对应。所以说，它们的数量是相等的！

你可能会说：「听上去不错。不过，这不就意味着，所有的无穷数都是一样大的吗？如果是这样，比较它们的大小还有什么意义呢？」

不，事情当然没有那么简单。人们可以很容易地找出比所有的整数或分数的个数还要大的无穷数。

现在回过头来，研究一下本章开头提出的问题。「一条线上所有点的个数」和「所有整数的个数」，到底谁大谁小？你会发现，这两个无穷数的大小确实是不同的——一条线上的点的个数要比所有的整数或分数个数要多得多。为了证明这一点，我们试着在一条线段上（比如说 1 英寸长），建立点和整数数列之间的一一对应关系。

线段上的每一个点都可以表示为它与线段某端间的距离，而且这段距离都可以记作一个无限小数，比如 0.7350624780056……，或 0.38250375632…… ^[2] 。现在我们就可以来比较所有整数和这些无限小数的个数了。那么，上面这些无限小数，和像、

这样的分数，又有怎样的区别呢？

大家一定还记得，我们在数学课上学过，每一个普通分数都可以转化成无限循环小数，比如

我们上面已经证明过，所有普通分数的个数和所有整数的个数是相同的，因此，所有循环小数的个数和所有整数的个数也是相同的。但是，一条线段上的点不可能完全表示成无限循环小数，而且大多数情况下，这些无限小数是不循环的。很容易看出来，在这种情况下，两个数列无法建立一一对应的关系。

假如有人声称，他能建立如下形式的对应关系：

当然，因为我们不可能写出无限不循环小数的每一位数，所以这张表的作者必定已经找到了某种一般性的规则（类似于我们将分数和所有整数进行配对的规则），并且按照这种规则构造了上面这个表，这种规则确保，我们所能想到的任何一个小数迟早都会出现在这张表里。

然而，不难证明，没有一种排列法则可以保证这样的事，因为我们总是可以写出一个没有出现在这个表里的无限不循环小数。如何办到的？再简单不过了只要让这个数的小数点后第一位数字和表里的一号数字（N1）的小数点后第一位不同，第二位数字和 N2 的小数点后第二位不同，依此类推，就会得到一个类似下面这样的数字：

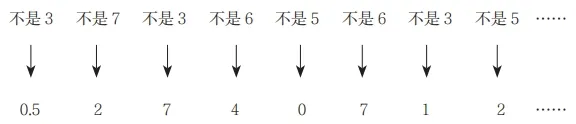
这样的话，无论你往下找多久，这个数字都不会出现在这个表里。如果这张表的作者告诉你，你写下的这个小数就在第 137 行（也可以是其他任意一行），那么你可以立刻告诉他：「不可能，因为这两个数在小数点后第 137 位上的数字是不同的。」

因此，一条线上的点的个数和整数的个数之间，无法建立一一对应的关系，这意味着， 一条线上的点的个数比所有整数或分数的个数更大，或者说更强。

我们一直在讨论「1 英寸长的线段」上点的个数，不过，根据「无穷数学」规则，很容易证明上述结论对任何一条线段上的点都适用，也就是说， 无论是 1 英寸、1 英尺，还是 1 英里，这些线段拥有的点的数目都是相等的 。想要证明这一点，只要看一下图 6 就可以。图上比较了两条长度不相等的线段 AB 和 AC 上的点的个数。为了在两条线之间建立一一对应的关系，我们从 AB 上的每一点出发，做一条平行于 BC 的线，并将它与两条线的交点进行配对，例如 D 和 D1、E和 E1、F 和 F1 等。如此一来，AB 上的每一个点在 AC 上都有点与之对应，反之亦然。因此，根据我们的规则，这两条线段拥有的点的数量是相等的。

在探索无穷大数的过程中，我们还有一个出人意料的发现： 一个平面上的所有点的数量和直线上点的数量竟然是一样的！ 为了论证这一点，我们来考察线段 AB（长度为 1 英寸）上面的点，和正方形 CDEF 内的点（图 7）。假设线段 AB某个位置上的点均可以用某数字来表示，比如说 0.75120386……，那么，我们可以由这个数字确定两个不同的数字，取小数点后的奇数位和偶数位重新组合，即0.7108……和 0.5236……。

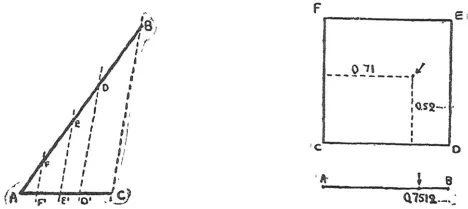
接下来，我们分别以这两个数字为横坐标和纵坐标的值，在正方形中寻找到对应的点，并把这个点称为此前线段上点的「对应点」。反过来，如果我们知道正方形里任何一个点的横坐标和纵坐标，打个比方，比如说 0.4835……和 0.9907……，通过相同的规则合并这两个数字，也可以得到它的「对应点」在线段上的位置：0.49893057……。

很显然，通过上述的步骤，两组点之间建立起了一一对应的关系。线上的每一个点都能在正方形里找到它的对应点，而正方形里的每一个点也能在线上找到对应。没有任何一个点会被遗漏。依照康托尔的规则，我们可以得出结论：正方形里所有点的数量等于线段上的所有点的数量。

使用类似的方法，也很容易证明，立方体内所有点的数量等于正方形或直线上点的数量。我们只需要把原来的小数拆分成三个新的数字 ^[3] ，然后用这三个数来定义立方体内「对应点」的位置即可。此外，就像两条长度不同的线段中，点的数量是相等的一样，无论正方形或立方体的大小如何，其中点的数量也不会改变。

虽然所有几何点的数量比所有整数或分数的数量要大，但它还不是数学家们已知的最大的无穷数。事实上，人们发现， 所有曲线的种类，包括那些最不同寻常的曲线，要比所有几何点的数量还要多，因此，必须要用无穷数列的第三个数来描述它。

根据「无穷数学」的开创者格奥尔格·康托尔的定义，无穷数可以用希伯来字母 ℵ （aleph）表示，其右下角有一个数字，表示它在无穷数列中的位置。由此，我们可以得到一个数字的序列（其中也包括无穷大数）：

1,2,3,4,5…… ℵ ₀ , ℵ , ℵ , ℵ ……

当我们说「一条线上有 ℵ 个点」，或「存在 ℵ 条不同的曲线」时，就和我们在说「世界分为七大洲」或「一盒纸牌有 52 张牌」时，没什么两样。

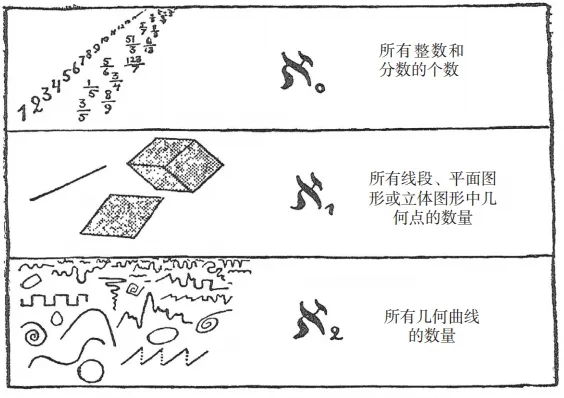
在结束有关无穷数的讨论之前，我们需要指出，虽然这些无穷数只分了几级，但是却包含了我们能想到的所有无穷大数。我们知道, ℵ ₀ 代表所有整数的个数， ℵ 代表所有几何点的数量， ℵ 代表所有曲线的数量，但是迄今为止，还没有人能够想出用来描述 ℵ 的集合。看来，前三个无穷大数就足以囊括我们所能想到的任何数字，这和我们的老朋友霍屯督人的处境刚好相反：他们明明拥有很多孩子，却最多只能数出三个！

注释：

[1] 这段内容从未正式发表过，希尔伯特甚至没有将它写成文字，但它流传甚广。引自 R. 柯朗，【大卫 · 希尔伯特轶事全集】。

[2]因为我们假定线段的长度是 1，所以这些小数全都比1小

[3]比如 0.735106822548312……这个数我们可以拆分为 0.71853……、0.30241……和 0.56282……。