梯度、散度、旋度是数学中的一个重要概念,在固体力学、流体力学、光学、电磁学等也有广泛的应用。本文旨在通过联系一些物理知识的学习,让大家更能深刻的理解梯度、散度和旋度。本文大致分为两部分,第一部分为一些相关数学知识学习,第二部分为相关物理知识介绍,希望对你有所帮助。
一、方向导数与梯度
1.数学定义。
方向导数本质上研究的是函数在某点处沿某特定方向上的变化率问题,而梯度反映的是空间变量变化趋势的最大值和方向。
以二元函数为例,方向导数的数学定义为:设函数z=f(x,y)在点P0(x0,y0)的某邻域U(P0)内有定义。自点P0引射线l,与x轴正向的夹角为α,如图所示。
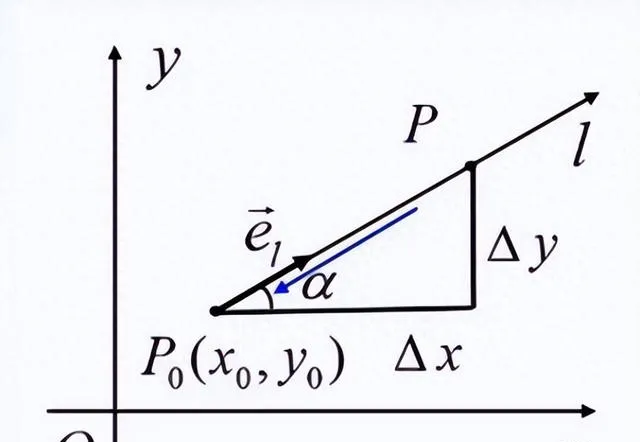
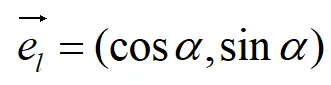
与射线l的同方向的单位向量
在l上任取一点P∈U(P0),坐标为:(x0+tcosα,y0+sinα)。当P沿着l趋于P0,即t→0+时,若如下极限存在,即:
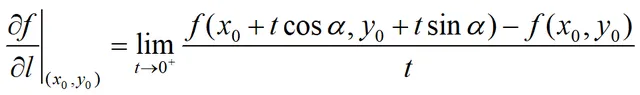
则称此极限为函数在点P0沿方向l的方向导数。如果函数z=f(x,y)在点P0(x0,y0)处可微,则函数在点P0(x0,y0)沿任何方向的方向导数均存在且有:
其中cosα,cosβ为射线l与x轴和y轴的方向余弦。以上结论可推广到三元及以上的多元函数。即:
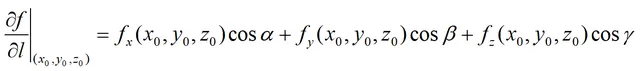
梯度的定义为:设函数z=f(x,y,z)在定义区域Ω内具有一阶连续的偏导数,对于区域Ω内的任意一点(x0,y0,z0),对应的向量:
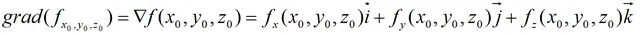
称为函数z=f(x,y,z)在点(x0,y0,z0)处的梯度向量,简称为梯度。其中▽称为哈密顿算子。
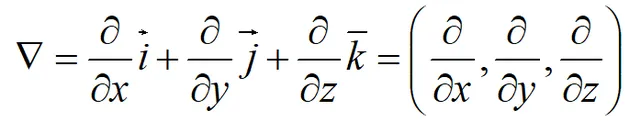
方向导数与梯度有如下关系:
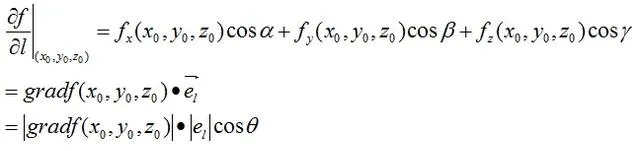
其中向量el为射线l的单位向量
显然:当射线l的方向与梯度方向一致时,方向导数取最大值,即梯度方向是函数增长速度最快的方向。当射线l的方向与梯度方向垂直时,方向导数在垂直于梯度的方向上值为零,即在此方向上函数的变化率为零。当射线l的方向与梯度方向相反时,方向导数取最小值。
2.方向导数与梯度的物理意义。
学完了大家是不是还是有点晕,这一堆公式到底表示什么呢?下面我们借助一些物理上保守力和势能的知识在进行说明,可能大家会有一些不一样的收获。
保守力是指其对物体做功只与物体的始末相对位置有关,和路径无关的力。典型的保守力有重力、弹力、万有引力和静电场力等。
势能是物体由于位置或位形而具有的能量,也可以释放或者或者转化为其他形式的能量。势能属于系统,是状态量,又称位能。可以规定某位置或位形为0势能位置,势能0点的选择和参考系无关。力学中势能主要有引力势能和弹力势能等。
二者间有如下的关系:系统的保守力所作的功等于系统势能减少,或等于系统势能增量的负值。即:
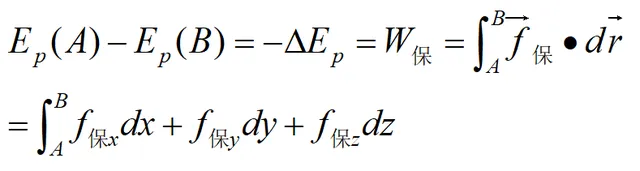
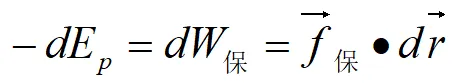
微分形式
反过来也可以由势能来求保守力。已知一质点受保守力,并沿某一方向移动,如下图,则保守力所作功和势能的关系如下:
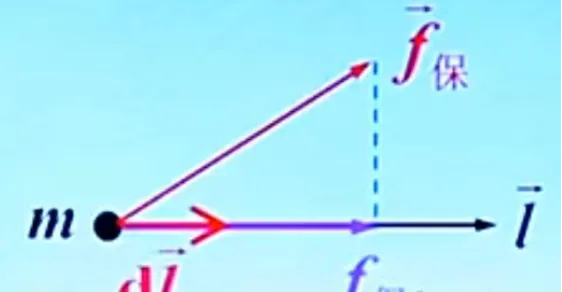
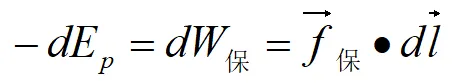
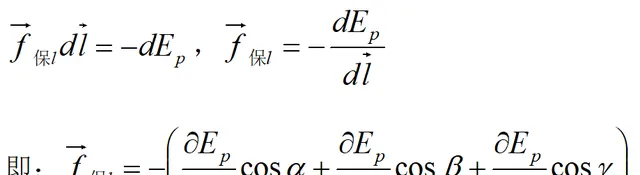
即在某点处,保守力沿空间某一方向的分量等于势能沿该方向的方向导数的负值。
显然当方向l与f保的方向一致或相反时,f保的分量的绝对值就是f保,达到最大。这与梯度的定义完全一致。
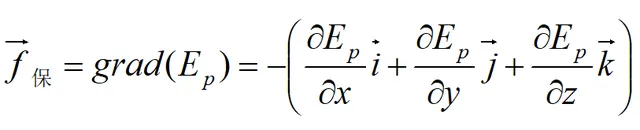
现在还需要解决一个问题,为什么保守力一定会存在一个对应的势函数呢?这是由于保守力做功与路径无关。这让我们想到了数学中对坐标的曲线积分与路径无关的四个等价条件的定理。设G是空间一维单连通域,函数P(x,y,z),Q(x,y,z),R(x,y,z)在G内具有一阶连续偏导数,则对于G内任意一点,如下四个条件是等价的。
1.对G内任一分段光滑曲线l,如下积分
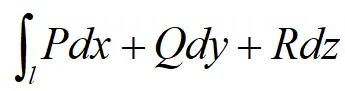
与路径无关。
2.若l是G任一分段光滑闭曲线,则:
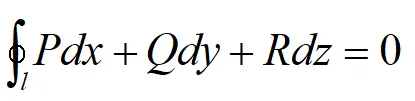
3.如下等式成立:
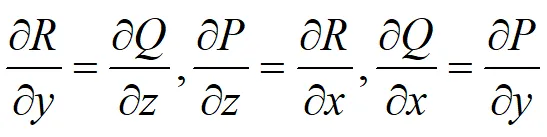
4.Pdx+Qdy+Rdz在G内是某一函数u(x,y,z)的全微分。
所以根据条件2,可得到一个推论:保守力沿任意闭合路径做功为零。
根据条件4,保守力做功与路径无关,必然存在:
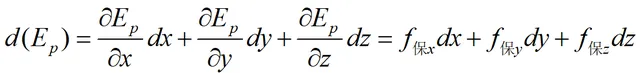
所以保守力必然存在一个势函数(标量函数)与之对应。
二、通量与散度。
1.数学定义。
设有向量场:
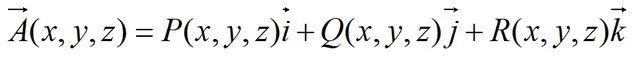
函数P(x,y,z),Q(x,y,z),R(x,y,z)有一阶连续偏导数,曲面Σ为场内的一片有向光滑曲面,n为Σ上的某一M(x,y,z)处的单位法向量。对面积的曲面积分:
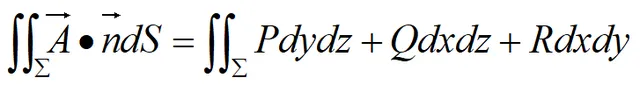
称为向量场A通过有向曲面Σ的通量(或流量)。
对向量场内任意一点M(x,y,z),数量函数:

称为向量场A在点M的散度。
2.通量与散度的物理意义。
通量的物理解释:即对稳定流动的不可压缩流体,速度场为:
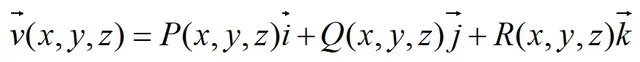
Σ为场中任一有向曲面,如下图:
则单位时间通过曲面Σ的流量为:
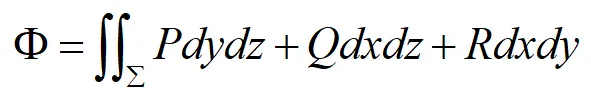
由两类曲面积分的关系可知,流量还可表示为:
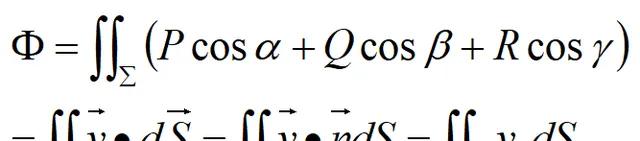
其中:vn为速度v在曲面法向量的投影。
散度的物理意义:令M(x,y,z)是某一流体流速场中任意一点,不难求得:
其中Φ表示通过速度场内某一封闭区域Ω的边界屈面Σ的通量。
根据高斯公式,上式可得:
根据积分中值定理,存在一点(ξ,η,ζ)∈Ω使得下式成立。
此式也给出了散度的另外一种解释,即散度是通量对体积的变化率,反应了流速场在点M的特点:散度值为正,负或0,分别反映在该点有流体涌出,吸入或没有任何变化。综上可知,散度是通量对体积的变化率,且有:
表明在该点处有流体流出,称之为源。
表明在该点处有流体被吸入,称之为汇。
表明在该点处无源无汇。
而散度的绝对值反映了源的强度。
三、环流量与旋度。
1.数学定义。
设有向量场:
函数P(x,y,z),Q(x,y,z),R(x,y,z)有一阶连续偏导时。Γ是向量场A的定义域内一条分段光滑封闭曲线,向量τ为曲线Γ在点(x,y,z)处的单位切向量,则向量场A中沿封闭曲线Γ上的曲线积分,称为向量场A沿有向闭曲线Γ的环流量。如下式:
以向量场A在坐标轴上的投影有关偏导式:
作为分量的向量称为向量场A的旋度,记作:
设曲面Σ是由Γ张成的一片有向光滑曲面,利用斯托克斯公式、两类曲线积分以及两类曲面积分的关系,向量场A的环流量和旋度有如下关系:
2.环流量与旋度的物理意义。
以平面流体为例,根据环流量的定义设有一平面流速场v在单位时间沿闭曲线L的环流量为:
其中:向量τ为曲线L某点的单位切向量,向量n为曲线L某点的单位切向量。
值得注意的是:我们一定要区分环流量与通量(流量)。环流量是流速沿切线方向对弧长的积分。而通量(流量)严格定义是曲面积分,但对于平面流体,可以理解为流速沿法线方向对弧长的积分,即上述流速场对于曲线L的通量Φ为:
旋度的物理意义:设某刚体绕定轴l转动,角速度向量为ω,M为刚体上任意一点,建立如图所示的坐标系:
则有:
点M的线速度
点M的旋度
也即旋度是角速度的2倍,同样该结论同样可以推广到三维空间。这也是「旋度」一词的来源。
下面再以一个例子直观的理解一下旋度的含义。
首先我们建立一个二维平面,即xy平面。假设速度场沿x方向速度分量是P(x,y)i,沿y方向的速度分量是Q(x,y)。xy平面中有一刚体。当x方向速度分量P(x,y)=0,y方向的速度分量Q(x,y)=常数时,如下图:
大家可以发现刚体将沿着平行于Y轴的方向运动,而不会发生旋转,那么我们说刚体的旋度是0。即:
即速度沿着刚体的方向x发生变化时,刚体将产生旋转,如下图:
四、哈密顿算子。
最后再谈一下前面提到过的哈密顿算子,哈密顿算子的引入可以使许多表达式显得简洁、美观,在数学、物理等都有广泛的用途。例如:
设f(x,y,z)为一函数,则梯度可表示为:
表示哈密顿算子作用于某一标量函数
设f(x,y,z)为一矢量函数,f(x,y,z)=[P(x,y,z),Q(x,y,z),R(x,y,z)],则散度可表示为:
表示哈密顿算子与一矢量函数的点积
设f(x,y,z)为一矢量函数,f(x,y,z)=[P(x,y,z),Q(x,y,z),R(x,y,z)],则旋度可表示为:
表示哈密顿算子与一矢量函数的叉积
梯度、散度、旋度的运算也表示了哈密顿算子的三个作用,即作用于标量函数,与矢量函数点积或叉积,可得到不同物理含义的表达式。
本文完,感谢你的耐心阅读。











