「中国孩子数学能力独步全球」,你是不是也曾将这样的神话误认为事实?
最近,一条关于留学教育的视频几乎火遍了各个平台,谈论的核心问题就是「数学」,只不过以视频中被采访者的经历来看,事实恰恰相反: 中国留学生的数学水平真心比不过美国大学生 。

「论计算,中国学生一等一」,但美国学生的学习更强调分析、推测等数学的底层逻辑,而这恰恰是中国学生所缺乏的,以至于去了美国之后往往反映数学吃不消……
同样提及国内数学教育与国际的差距,几年前,中国科学院物理所研究员曹则贤教授在中国科学技术大学的演讲中所列出的数据则更加惊人,他说, 85%的数学知识从来没有传入到中国 。
这也能从一定程度上解释,为什么大家的「数学焦虑」会如此普遍而深重:微博上与数学有关的话题达到了5.9亿人次的阅读;而抖音里,数学的话题播放量高达541亿次,平均每个中国人都要观看至少38条关于数学的视频。
数学为什么难学?为什么让绝大多数接触到它的人感到恐惧?
今天,阿信要向所有被数学折磨,以及对数学感兴趣的小伙伴强烈推荐一本能补齐数学知识拼图的新书——
【数学的逻辑】
。

作者是剑桥大学数学博士、芝加哥艺术学院常驻科学家
郑乐隽
。
「消除世界上所有人对数学的恐惧」是郑教授终身奋斗的事业目标。为此,她写作了【超越无穷大】【数学思维】【逻辑的力量】等多部数学科普畅销书,被英国【卫报】曾授予「科学与自然类新秀作者」奖。
同时,她还是一位举办过音乐会的钢琴家,能够流利用法语、英语和广东话交流。
在这本书中,她讲告诉你,数学的核心,从来不在于计算出正确结果,数学是一整套思想的集成,逻辑在其中起着至关重要的作用。
掌握了数学的逻辑,你会发现,数学并不枯燥,相反,它与我们生活中的方方面面都息息相关,用数学思维观察世界,你会获得一种全然不同的视角。
郑乐隽:从厌学少年到数学达人
和很多普通人一样,
郑乐隽
对数学也是有厌学情绪的:
我和它的感情在小学阶段不断恶化,到了初中我开始彻底厌恶这门学科,因为我觉得它既乏味又迂腐。
我一点儿也不责怪我的老师,这都是课程设置和考试制度的问题。

郑乐隽
但她也和很多人一开始一样,忽视了一个重要的信息:人们讨厌数学往往是因为找不到正确的答案而觉得自己很愚蠢,并不是讨厌寻找的过程。
所幸,她找到了自身原因。
在她开始接触少许高等数学之后,情况有了一些改观,尤其是普通中等教育证书(GCSE)的研究项目令她对数学钟爱有加。
那都是一些开放性的课题,每个学期需要花费几周的时间来完成。我们从一个结构严谨的问题出发,独立探索由它引发的无限可能性。
直到上了大学,事情才真正开始好转。等到郑乐隽开始攻读博士学位时,她对数学的喜爱程度已经超过了图表所能表示的范围。当然,那个时候她们已经不再上课,而是通过阅读、集体讨论、参加研讨会来学习。
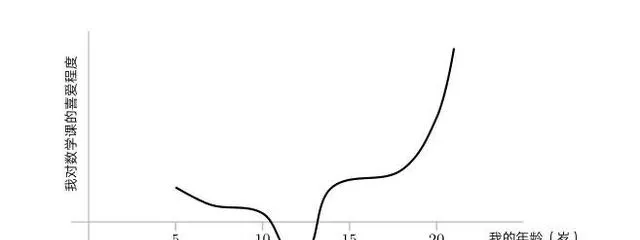
郑乐隽对数学的喜爱程度变化。图:【数学的逻辑】
在她之后的人生里,数学成了
她的爱好,而不是苦难,她将这些经历写成了【数学的逻辑】
。

【数学的逻辑】都在说啥?
在【数学的逻辑】的开篇,郑乐隽就帮助大家撇清自己的「愚笨」。
我想要告诉你,如果你觉得自己不擅长数学,或者在学校里被认为数学成绩很糟糕,那么完全有可能你只是在探寻对数学更深层次的理解,而身边没有人能帮助你达到那个水平。
在前面4章,她都是从广义的数学概念讲起,然后聚焦数学中的一些具体的问题,以故事的形式给大家科普:数学从哪里来、数学的逻辑、为什么要学习数学、什么是好的数学……
在5、6、7三章,她会聚焦具体的数学工具,给大家介绍字母、公式和图形。
第8章,她用一个貌似天真、有时也被视为「愚蠢」的问题开始讲故事,然后通过对这个问题的深入探究把我们引向一项重要的数学研究。
接下来,我们来看看这本书具体讲了什么。
比如在【图形】这一章,讲到很多女孩子对于编发辫感兴趣,尤其是对如何编出发辫的不同图案感兴趣。下图左右分别是法式辫子和瑞典式辫子。

很多人以为这只是一个生活技巧,却不知道,编发和数学中 高维度范畴论 研究有很大的关系,这项理论研究的出发点就是基于我们不仅关心某物是否发生了互换,而且关心互换的具体方式。
尤其是放到抽象数学领域,我们会研究一般意义上的交换律。尤其是空间交换所带来的结果是一样的,比如下面两张图。
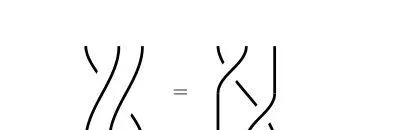
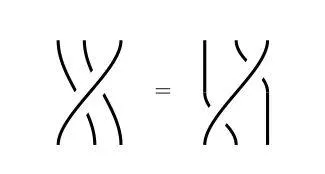
虽然空间发生了位移,但是实际上的编发效果是一样的。从结果来说,这就是我们在数学中认定辫子结构「相等」的含义,即它们之间的差别仅仅在于移动和拉紧,而与解开和重新缠绕无关。
对数学来说,重要的是证明图形推理具有逻辑上的正确性。这也是范畴论中关于证明逻辑与直觉相互对应的重要性。

生活中处处都充斥着数学
生活中很多很简单的案例背后常常有高深的数学的理论,只是我们并不知道「这属于数学」。
举一个看起来天真实际能引发深刻意义的数学问题。一个圆有几条边?
大多说人会觉得,圆就是一条封闭的曲线,是一条边。
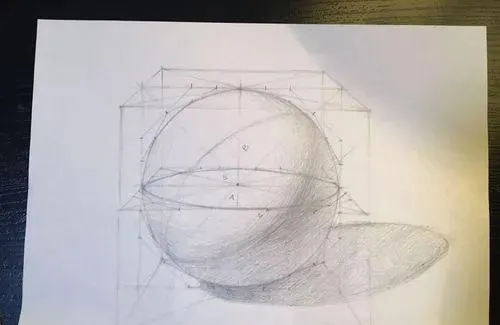
但是学会微积分的人知道,圆是通过无数次切割得来的接近「圆」这个概念的,学素描的人画圆的时候,最规矩以及最保险的模式也是通过正方形进行无数次的切割得到想到的结果。
所以圆上其实是存在无数条切割的「小边」的,这个边,可以是无穷个。
再举例一个我们生活中的案例。
你觉得一根吸管有几个洞?
和往常一样,我们对这个问题产生数学上的兴趣并不在于答案究竟是什么,因为从不同的角度出发能得到不同的正确答案。
真正有趣的是,我们可以用不同的方式来思考洞以及吸管的问题。于是我们回到了计数的方法上:首先,什么才是可被统计在内的对象;其次,什么时候两个对象实际上是相同的。

常规认为,立体角度上吸管只有一个洞,计数为1。但是从平面上看,左右两边都是洞,计数为2。重新回到立体角度上,如果吸管内部空间和外部相连,那吸管实际是一个洞都没有,计数为0。
而从分子角度考虑问题,吸管放大到无穷大,分子之间是有很多空隙的,所以吸管有无数个洞,计数为∞。
因此,
沿袭以往的数学思想,关键不在于判断哪个答案是正确的,而是要确定它们在何种意义上是正确的
。
如果觉得一根吸管只有一个洞,我们该怎样定义洞?同样,如果觉得一根吸管有两个洞,我们就必须采纳另一种洞的定义。那我们该怎么做呢?
拓扑学是专门研究形状的数学分支,它依据一种特定的「相同」理论判断哪些形状与另一些形状相同。它来自将一个东西逐渐变形为另一个东西的过程。

比如探究吸管只有1个洞的时候,从拓扑学上,我们可以借用甜甜圈的例子。看起来两个实物没有什么关联,但是如果我们用手指压扁它的内侧壁,最终,甜甜圈会变成一个圆筒,然后我们将其拉长,就变成了一个吸管。
从这个意义上看,吸管的确只有一个洞,我们也可以想象吸管变得越来越短,直到变成一个圆圈,它的中间只有一个洞。
这只是拓扑学研究洞的方法之一。数学家一般不使用「洞」这个名称,因为我们发现它相当模糊。而且在某些情况下,我们的直觉并不喜欢拓扑学做出的解释。
所以这本【数学的逻辑】会从根本上让你知道数学不仅仅是工具,也不仅仅是枯燥的公式,更不是为了验证你是否聪明的道具。
喜欢数学的人也仅仅是「喜欢数字」「喜欢公式」或乐于找到正确的答案不同。
郑乐隽更想告诉大家的是:
人们厌恶数学的原因是非常不幸的,并不是基于数学真正的本质
。
那些天真、开放、「愚蠢」的数学问题绝对是有意义的,它们都是好问题,这样的问题在数学研究过程中是不可或缺的。
数学,更多的是帮助我们找到找到事物之间关系,也因此能帮助我们发现世界的真相。
*商务合作、高管学习请添加:墨墨老师138 1108 2512 (微信同步)











