
统计学是数据分析的基础理论,但统计结论往往存在一些"坑"。面对统计结果,我们需要仔细分析和避免常见的错误,其中包括将数理关系误认为因果关系、不同变量之间可能存在悖论,以及数据统计可能受到偏差的影响。
在众多悖论中,伯克森悖论( Berkson's Paradox )是其中之一。它指出在处理数据时,容易因为未能全面了解整个情况而误以为两个事物存在关联。这种错误可能对机器学习专家的预测模型准确性产生重大影响,因为它导致了对变量之间关系的错误假设。
通过一个例子来解释,例如,我们假设某学生的文化成绩较高,那么他的体育成绩就较差;反之,体育成绩越好,文化成绩就越差。这似乎已经成为我们日常观察中的一种认知,即班上的尖子生好像体育成绩普遍不太出色。那么,这种现象是如何出现的呢?
设想学生需要参加两种类型的考试,即文化和体育课,其中只要在任何一种类型的考试中获得90分以上就能顺利毕业。因此,毕业的学生要么在文化考试中取得90分以上,或者在体育考试中获得90分以上,或者在两门考试中都取得90分以上。通常情况下,正常人只需专注于其中一门考试,充分发挥至极致即可,而对另一门考试不太重视。因此,学生的文化成绩和体育成绩会呈现负相关的关系。
伯克森悖论还能解释为什么很多人都认为帅哥通常是渣男,以及为什么颜值超高的小鲜肉演员演技不尽人意,这些现象。
举个数值事例说明伯克森悖论
为了说明伯克森悖论( Berkson's Paradox ),接下来使用两个骰子:
这两个事件显然是独立的,其中 P(X)=1/6 而 P(Y)=1/3。
现在,让我们引入条件(Z),表示通过 第一个骰子是 6 点且第二个骰子是 1 点或 2 点的所有结果而引入的抽样偏差。
在我们的有偏抽样条件下,我们需要计算事件 X 发生的概率,假设至少其中一个事件(X 或 Y)发生,这由 P(X|Z) 表示。
首先,我们需要确定 Z = (X ∪ Y) 的概率(即在已知第一个骰子是 6 点或第二个骰子是 1 点或 2 点的情况下,第一个骰子出现 6 点的概率):
P(Z)=P(X∪Y)
=P(X)+P(Y)−P(X∩Y)
=P(X)+P(Y)-P(X)×P(Y)
=1/6+1/3-1/6×1/3
=4/9
接下来,我们计算给定 Z 的 X 的概率:
P ( X ∣ Z ) =P(X∩Z)/P(Z)=P(X)/P(Z)
=1/6 / (4/9)
=3/8
=0.375
为了查看在 Z 发生的假设下 X 和 Y 之间是否存在依赖关系,我们必须计算(已知第二个骰子是 1 点或 2 点的情况下,同时第一个骰子是 6 点的情况下,第一个骰子出现 6 点的概率):
P(X | Y ∩ Z) ≈ 0.1666…
上述数据确实得到了伯克森悖论的特性,由于抽样偏差 Z,我们有 P(X | Z) > P(X ∣ Y ∩ Z)。
是不是这相当令人惊讶!我们有两个骰子…两个明显独立的随机事件…通过一个抽样过程,我们会产生骰子点数变得相互依赖的印象。
Python模拟掷骰子的过程复现伯克森悖论
在下面的代码中使用Python模拟掷骰子的过程。
以下代码模拟了一百万次掷两个骰子的实验,在每次实验中,它检查第一个骰子是否掷出6点(事件X),以及第二个骰子是否掷出1点或2点(事件Y)。然后,它将这些检查的结果(True或False)分别存储在列表X和Y中。
import randomdef sample_X_Y(nb_exp): X = [] Y = [] for i in range(nb_exp): dice1 = random.randint(1,6) dice2 = random.randint(1,6) X.append(dice1 == 6) Y.append(dice2 in [1,2]) return X, Ynb_exp=1_000_000X, Y = sample_X_Y(nb_exp)
以下代码计算了事件X的概率和在事件Y发生的条件下事件X的条件概率。它通过将成功的结果数量除以每个概率的总实验次数来完成这个计算。
p_X = sum(X)/nb_expp_X_Y = sum([X[i] for i in range(nb_exp) if Y[i]])/sum(Y)print("P(X=1) = ", round(p_X,5))print("P(X=1|Y=1) = ", round(p_X_Y,5))
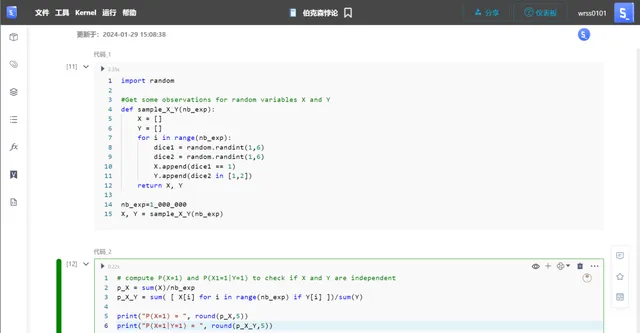
正如所看到的,这两个概率是接近的;因此两个骰子是独立的。
现在,让我们看看在引入抽样偏差Z时会发生什么。下面的代码过滤了实验的结果,仅保留那些其中X = 1,Y = 1或两者都为1的结果。它将这些过滤后的结果存储在列表XZ和YZ中。
XZ = []YZ = []for i in range(nb_exp): if X[i] or Y[i]: XZ.append(X[i]) YZ.append(Y[i]) nb_obs_Z = len(XZ)
现在,检查一下这些新变量是否仍然是独立的。
p_X_Z = sum(XZ)/nb_obs_Zp_X_Y_Z = sum([XZ[i] for i in range(nb_obs_Z) if YZ[i]])/sum(YZ)print("P(X=1|Z=1) = ", round(p_X_Z,5))print("P(X=1|Y=1,Z=1) = ", round(p_X_Y_Z,5))
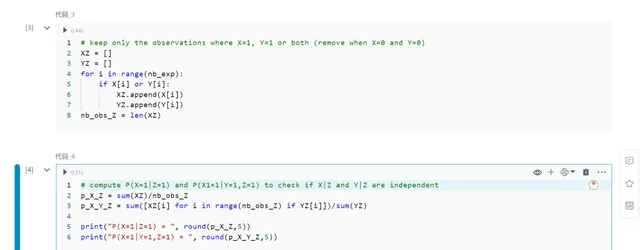
这意味着如果Z为真,则拥有关于Y的信息会改变X的概率;因此,它们不再是独立的。
伯克森悖论悖论对机器学习的影响
现实中,数据科学家或算法工程师们并没有足够关注这种类型的偏差。伯克森悖论悖论涉及到了我们如何被我们使用的数据误导的问题。伯克森悖论警告我们关于使用有偏或片面数据的危险。
在每种情景中,忽视伯克森悖论可能导致有偏的模型,影响决策和公平性。机器学习专家必须通过多样化数据源并不断验证模型与实际场景相匹配,以抵消这种影响。
总而言之,伯克森悖论是机器学习专业人士提醒他们审查数据来源并避免误导性相关性的重要提醒。通过理解和考虑这一悖论,可以构建更准确、公平和实用的模型,真正反映现实世界的复杂性。记住,健壮的机器学习关键在于精密的算法和对数据的深思熟虑、全面的收集与分析。











