这里的X是一个集合，R是X上的一个σ代数。
意思是说，集合Ā是由集合A再并上集合E构成的，而且集合E的测度为0。
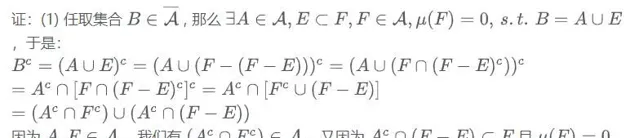
以上内容不难理解。
以上是把集合B拆分为无穷多个，结论仍然成立。
这个定理的意思就是，当A这个σ代数再加上测度为0的集合以后，还是一个测度空间。
比如，假设X是无理数集合，A是X上的一个σ代数。这个时候如果再把有理数加入集合A构成集合Ā，则(X,Ā)还是一个测度空间。
这个定理是测度扩张的基础。
测度扩张的一个基础定理
这里的X是一个集合，R是X上的一个σ代数。
意思是说，集合Ā是由集合A再并上集合E构成的，而且集合E的测度为0。
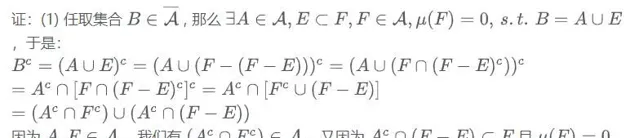
以上内容不难理解。
以上是把集合B拆分为无穷多个，结论仍然成立。
这个定理的意思就是，当A这个σ代数再加上测度为0的集合以后，还是一个测度空间。
比如，假设X是无理数集合，A是X上的一个σ代数。这个时候如果再把有理数加入集合A构成集合Ā，则(X,Ā)还是一个测度空间。
这个定理是测度扩张的基础。
Copyright © 2024 www.aqiusha.com NO.1 华文世界
商务合作：xingwa#jasve.com（发送邮件请将#换成@）
