二重积分中值定理的几何意义可以理解为:在特定的有界闭区域上,存在一个点,其函数值乘以该区域的面积等于整个闭区域上函数的二重积分值。
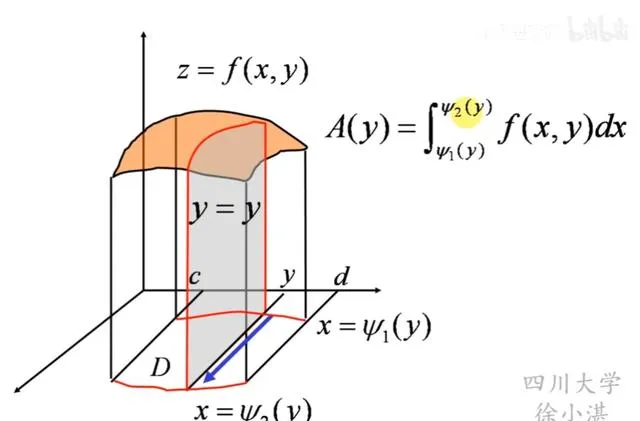
具体来说,这个定理表明,对于一个在闭区域D上连续且有界的函数f(x,y),存在一个点(c,d)属于D,使得f(c,d)乘以D的面积等于对D进行f(x,y)二重积分的结果。这个定理的几何意义在于,它将复杂的二重积分问题转化为了寻找一个特定的点,这个点的函数值能够代表整个区域上函数的平均水平。
从直观上讲,如果我们想象函数f(x,y)在区域D上的变化类似于一个起伏的地形图,那么二重积分中值定理告诉我们,在这个地形中存在一个「平均高度」的点,这个点的高度乘以整个区域的面积,与把整个地形覆盖一层土壤,使地形完全平坦后的总体积相等。
在应用上,这个定理非常有用,因为它允许我们通过计算一个点的函数值来估计或近似整个区域的积分值,这在解决实际问题时可以大大简化计算过程。例如,在物理学中,当我们需要估算某个区域的平均温度或者压力时,就可以通过找到这样一个代表性的点来进行测量和计算。











