[CSP-J 2021 T4] 小熊的果篮
正文开始
本题的题意还是非常容易理解的。把每个「水果块 」的第一个水果的 编号 输出,另 外取走水果后如果相邻水果块种类相同,还要考虑这两个水果块 合并 的问题。
老规矩,做题前先看数据范围:

「提示」很友好,不多见。国人出题擅长挖坑,主动提示避坑的少之又少.
骗分
显然,对于 的数据点, 暴力求解 就可以。每次从队首 开始扫描,只要 与前一个块的水果 (用 last 记录,第一次赋值为-2 ,确保跟数组中的所有值不一 样)不一样,就输出 编号 ,并顺便把已输出的水果标记为-1 (表示该位置水果已 经被取走),下次扫描碰到-1 就跳过。如果一共输出了 n 次(用 cnt 记录),说明 把所有水果都输出了,结束!
代码如下:

提交后:
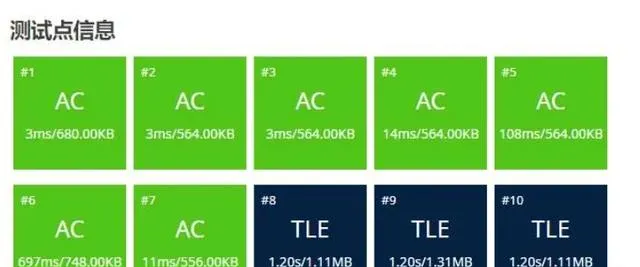
居然有 70 分!成功来得太突然!本来只是随便玩玩,结果离 AC 只差了 3 毫米!
那么为什么 n<=50000 的数据也能过呢?说明每次 for 循环中,输出的 i 次数比 较多,cnt++ 不断执行,所以外层的 while(cnt <n) 执行次数不多,应该不超过2000 次 。如果有一个数据点,全部都是 1 ,或者全部都是 0 ,上述算法应该是过 不了的。
对于这道题,除了这么简单的做法,很多同学可能会想到用链表 list 。每次拿走 一个水果,就把它从链表中删除,那么下次再继续从头扫描的时候,链表已经变 短了,从头到尾扫描的次数会越来越少。但实际上,这种做法,跟我们上面用数组暴力检索 没有太本质的区别 。不信我们来写一下用链表 list 做这道题:
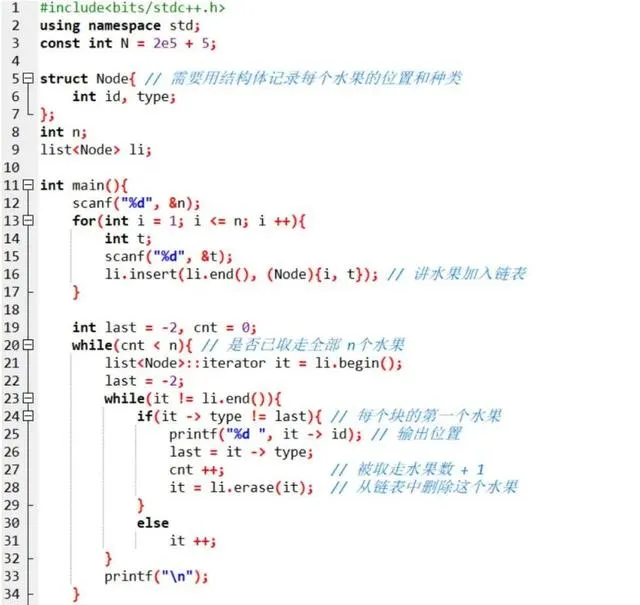
提交后也是 70 分:

超时的最主要原因,是每一个「 块 」中间大量不用输出的节点,也遍历了一遍,花 了很多时间。能不能想一个办法,对于每个块,只访问「 块 」头的元素。输出「 块 」 头的元素的编号后,就接着访问下一个「 块 「。
思考
我们可以这样处理,把每个「 块 「作为数据处理点,把」 块 「的第一个元素的编号 (标 记为:L )和最后一个元素的编号 (标记为:R ),以及」 块 「的水果类型(标记为:type )记住,然后这些水果就按」 块 「进行排列了。
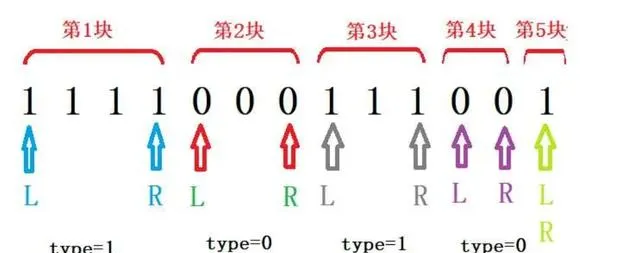
」 块 「的数量,可能就比水果的数量少很多,这会使得循环时需要遍历的次数少一 些。
由于每循环操作一次后,要输出换行,所以我们特意加了一个所谓的 末尾块 。在 每一轮结束后,如果检索到了 末尾块 ,那么输出回车。 末尾块 每次都要 push 进 队列,所以当水果都取完的时候,队列的 size 应该是1 。
代码如下:
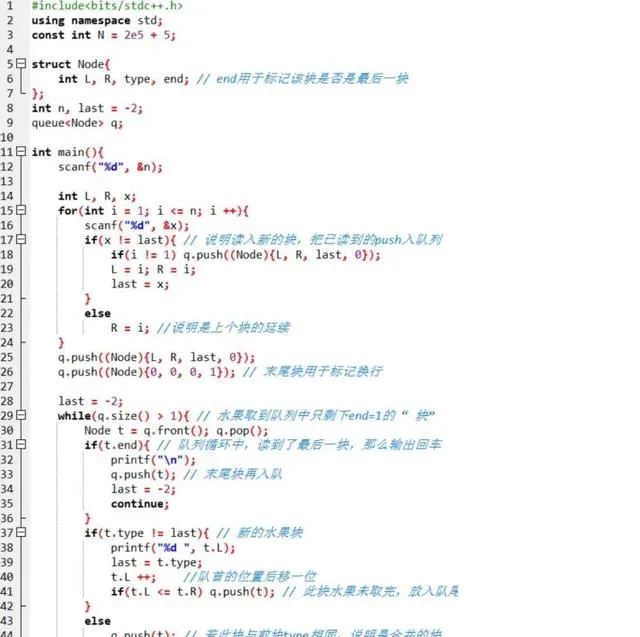
提交后:

多了宝贵的 10 分!不容易啊!
思考一下,为什么会超时?假设有很多 块 ,其中只含有一个水果,那么它被取走 后,它 后面的水果块 应该与 前面的水果块 合并,但是按照我们上述代码,实际上 并没有合并,而是直接 push 进入 queue 后面,而且每一轮都如此。那么如果碰 到与前一块 type 相同的块,数量非常多时,是非常耗时的。整个复杂度为 O (), 过不了关。
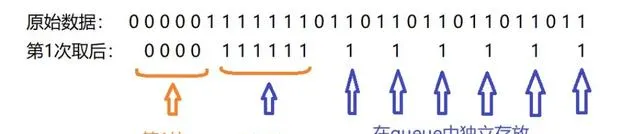
如上所示,第一次取后,后面那些 1 ,是独立的块 ,但它们应该和第 2 块合并。这些 1 很晚才会被取走,因为没合并,所以每次需要不断地取出并重新 push 入queue ,非常耗时。
AC
那么,我们能否想个办法,当发现前后的块 ,type 相同时进行合并成一块?这个 想法的难点在于,合并后的主要信息( 编号 )是离散的,不是连续的,如果要用数组 或 vector 保存,需要把每个编号 都保存下来,这增加了内存开销。我们需要另外想一个办法。
我们的解决办法是另外设一个 临时的队列 tmp 。每轮取走水果后,如果块 中还有 水果,则把该块放入临时队列 tmp 。然后,对 tmp 进行集中处理,合并其中水果相同的块 (我们只需要 把前面块的右端点延长到后面块的右端点即可实现合并 ), 再 push 进队列 q 中。这时候,q 中原本很大的 size 会大大下降,因此能大幅 降低算法复杂度 。另外,合并后的块,未取走的水果编号不连续的问题,可以通过t.L 单向移动来解决。
最终这个算法复杂度是多少?由于 t.L 总是是从左往右单向移动,而且每轮必定 会从这些块中各取走 1 个水果,因此复杂度大约是 O(n) 。
代码如下:
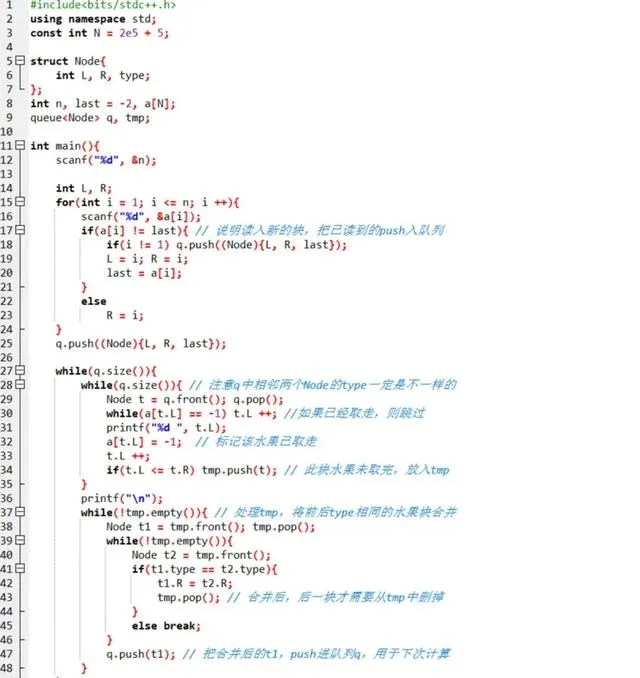
提交后,果然 AC!

总结:
这道题我们开始的时候用最简单的数组保存,并且暴力枚举 ,居然就得了 70 分。这种方式每次都从头到尾扫描 n 次 ,显然太复杂,所以我们按「块」对数据进行 处理,不需要每次扫描 n 次,只需要扫描块数(一般情况下比 n 小) ,但本质上也没有大幅降低复杂度,因为「零碎」的块可能很多。因此我们又单独引入另外一个队列 ,专门处理「块」的合并 ,这样就快多了.












