函數在科學和經濟學領域中扮演著重要角色,它們幫助我們理解自然規律、分析數據和預測趨勢。本文將詳細介紹牛頓的萬有重力定律、笛卡爾的解析幾何以及經濟學中的供需關系和成本曲線,並透過例項分析,幫助讀者更好地理解函數的套用。
I. 牛頓的萬有重力定律
牛頓的萬有重力定律是描述物體之間重力相互作用的重要定律。根據這一定律,地球上物體施加的重力與物體質素成正比,與兩個物體之間距離的平方成反比。這可以用公式表示為:F=G*m1*m2/r^2。
例如,當我們投擲一個物體時,地球的重力使其受到向下的加速度。根據牛頓的定律,我們可以計算出物體所受的重力,並預測其運動軌跡。這個定律還可以套用於星系中星體的運動和重力相互作用等領域。
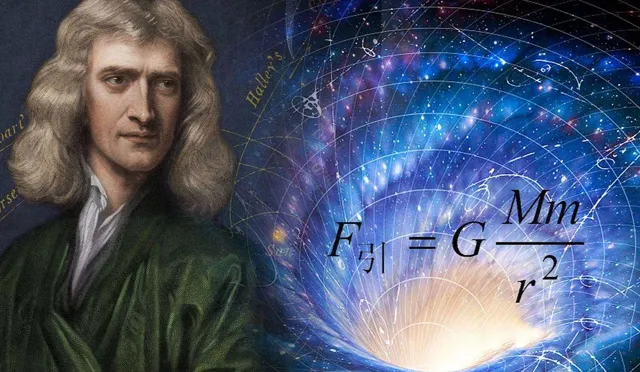
II. 笛卡爾的解析幾何
笛卡爾的解析幾何將幾何問題轉化為代數問題,為我們提供了一種方便的方法來描述幾何圖形。他引入了座標系的概念,使得我們可以用代數方式解決幾何問題。
在笛卡爾座標系中,我們可以用點的x和y座標來表示其位置。例如,對於一個直線,我們可以用一次函數y=mx+b來表示其方程式。透過使用這些函數,我們可以計算直線的斜率和截距等資訊,並進一步研究多條直線之間的關系。
III. 經濟學中的供需關系和成本曲線
函數在經濟學中也有廣泛套用,特別是在描述供需關系和成本曲線方面。
1. 供需關系:供給函數描述生產者願意在某個價格下提供多少商品,而需求函數描述消費者願意在某個價格下購買多少商品。當供給和需求的函數相遇時,就會形成市場的均衡價格和數量。透過對供需關系的分析,我們可以預測市場的變化趨勢,幫助決策者做出合理的決策。
2. 成本曲線:成本曲線描述了生產一定數量的商品所需的成本。它包括固定成本和變動成本兩部份。固定成本是在生產過程中不變的成本,例如租金和器材費用,而變動成本隨著生產數量的增加而增加,例如原材料成本和人工成本。透過分析成本曲線,我們可以估計生產特定數量商品的成本,並制定相應的生產決策。
【奇妙數學史:數碼與生活】本書從歷史的視角向我們娓娓講述數碼迷人的發展史,從數碼的發明到各種運算子號,從零的出現到超越數的神奇,從十進制到現代的消息理論,從第一台電腦的發明到人類計時的方式,展示了數碼是如何從生活中來,又是如何影響著我們周圍的方方面面的。本書將帶你踏上全新的旅程,走進美妙的數學世界
結語
函數在科學和經濟學中具有廣泛的套用,幫助我們理解自然規律、分析數據和預測趨勢。牛頓的萬有重力定律、笛卡爾的解析幾何以及經濟學中的供需關系和成本曲線都是函數在各個領域的典型套用案例。透過對這些套用的深入分析,我們可以更好地理解函數的重要性,並在實際套用中做出合理決策。











