
開啟愉快的旅程
生活中,我們會遇到很多不斷「連續變化的量」,例如我們開車上路時,汽車的裏程是在連續不斷變化著的,裏程表上的公裏數值一直在上升。雖然某一時刻都對應著一個具體的裏程值,但這個裏程值並不是孤立存在的,它有變化能力,這個變化能力具體是多大呢?

裏程在上升,上升得有多快呢?
我們可以看下速度表,某一時刻速度表上的數碼,就是該時刻裏程的變化能力,這個變化能力我們也稱之為「變化率」,例如一小時能上升30公裏的裏程。

速度就是裏程變化快慢的度量,即裏程的變化率
數學的角度,怎麽計算出這個變化率呢?如果汽車是直線勻速行駛的,我們只需用小學的除法,就可以簡單計算出來:總裏程÷行駛所用時間=速度,速度就是某時刻裏程上升快慢能力的具體數值。

勻速運動,用普通除法就能算出變化率
現實中車輛的速度,是時快時慢的,要求出某個時刻的對應速度,普通除法搞不定(普通除法只能得到速度的平均值),這時就需要用到更高一級的特殊除法:導數。導數是把除法加入極限思維後的一種計算方法,目的就是用來求出變化率。
還是以汽車的裏程變化快慢為例,總裏程÷行駛所用時間=平均速度,這個比值關系式裏,如果「行駛所用的時間」無限接近零,那麽所求出的比值,就無限接近該時刻的真實速度值,也就是計算出這個比值在分母部份趨於零時,無限接近的那個數值,就得了速度。這種計算比值極限的方法,就是導數。
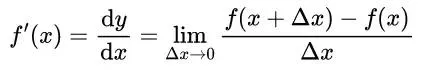
導數的定義
求出汽車裏程的導數,就得到了速度。
那裏程的微分,又是什麽呢?用某時刻對應的速度,乘以一段時間的改變量,就是該時刻裏程的微分,例如在行駛到0.5小時的時候,假設此時對應的速度為56公裏每小時,則此時刻對應的裏程微分運算式,就是:此時刻路程的微分=56×時間改變量,時間改變量的值可以任意取,例如取0.3小時,具體的微分值就是56×0.3=16.8,註意汽車繼續行駛了0.3小時後,實際的裏程並不一定是16.8公裏,因為速度是變化的,而不是一直保持在56公裏每小時不變,所以某時刻裏程的微分,就是以該時刻的速度為基礎,所計算出來裏程變化量的近似值,這個近似值與真實值顯然存在著誤差,當時間改變量的取值無限接近接近零時,這個誤差也將無限接近零,而且它接近零的程度,比時間改變量自己接近零的程度還厲害,數學上稱為「更高階」。從函數影像上看,某時刻裏程的微分,就是裏程函數的曲線,在該時刻的切線的上升高度。
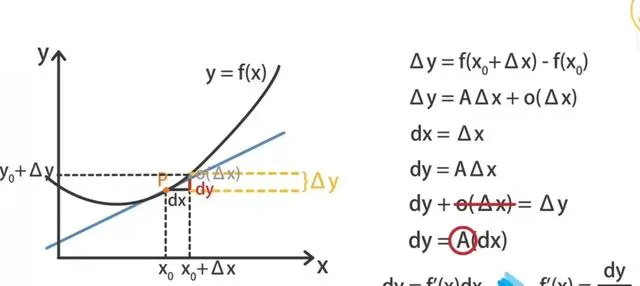
函數曲線上某點對應於自變量改變量的微分,就是該點切線的變化高度dy,它是曲線實際變化高度△y的近似值
利用裏程的變化率,也就是速度,得出微分運算式後,就可以反過來可以求出實際的裏程,方法就是「積分」運算 ,也就是變化率的逆運算——求出原函數,類似於乘除法互為逆運算,其實乘除法可以看成是微積分運算的特殊情況,即在變化率固定不變時的運用。

數學 ,就是這麽有趣。











