女士們,先生們,老少爺們兒們!在下張大少。
圖形、數學和非洲
圖論是數學的標準組成部份。一個經典的例子是尋找一個推銷員存取美國50個州的所有首府一次所需的最短路徑。這個所謂的「旅行推銷員」問題至今仍是一個未解之謎,盡管已經有了幾個「好」的解決方案。兩個城市之間的「路徑」可以用直線表示,如果方向也很重要,還可以加上箭頭。線的形式可以是直線,也可以是粗略畫出的曲線,但這並不重要。圖論的套用有時是運籌學課程的一部份,從經濟學到電腦科學,圖論的套用不勝列舉。
大多數運籌學教科書的入門例子都提到了歐拉的七橋問題,即如何走過前德國城市哥尼斯堡的七座橋。如今,哥尼斯堡已成為俄羅斯的加利寧格勒市,七座橋也已不復存在,但在七座橋還存在的時候,歐拉就已經證明,如果同一條路徑不能走兩次,就不可能走過七座橋。
一個重要的數學特點是,可以利用這些圖形進行計算,讓數學家獲得直觀無法發現的驚人結果。例如,對歐拉圖進行數學研究時,可將左邊的三個點從上到下編號為 1、2、3,並為右邊的點加上數碼4。在一個稱為矩陣的列表中,1表示從該行前面提到的點到該列上面提到的點之間有一條路徑。如果沒有路徑,則使用0。在給出的範例中,主對角線上有0,因為點本身沒有迴圈(圖4.1)。

圖4.1:沙地版歐拉問題(左)及其數學版(右)
圖論的數學力量並非源於歐拉走橋的趣聞軼事或其他有趣的素描,而是源於使用這些「矩陣」的數學技術,從而可以得出結論,而這些結論在糾結的線條中是無法預測的。這一數學版本的優勢體現在它的許多套用中,例如四色定理(四種顏色足以為任何地圖著色,使得沒有兩個相鄰的國家是相同的顏色)。
非洲的例子也可以作為圖論的入門。世界各地的不同文化都會用手指或樹枝在沙地上作畫,或擡手或不擡手,充滿曲折的線條增強了其神話色彩。有時還會加上一些符號,以明確繪畫的目的。這表明,不僅舞蹈、音樂或戲劇表現是儀式的靈感來源,數學方案也是如此。
關於非洲圖形的故事
來自剛果和安哥拉邊境地區的紹奎人稱他們的沙畫為 「sona」。在村子中心舉行的集會上,他們會朗誦這些圖畫上的故事。在長達6-8個月的啟蒙儀式中,每一代人都要學習這些傳統圖示以及相應的諺語、背誦內容或謎語。
有時使用這些圖畫的另一個場合是哀悼儀式。據說一個村長死了,有三個候選人來繼承他的職位。一幅幾何圖畫代表了這種情況:中間一個大白點代表死去的酋長,另外三個小黑點,分別編號為1、2和3。一條封閉的曲線環繞著三位王位繼承人和死去的首領。其中兩個候選人在不越線的情況下無法到達死去的酋長身邊,但中間的那個候選人可以,因此他成為了新的酋長。在另一幅圖中,一條單線將新生兒和逝者連線起來,太陽和月亮在每個凡人的生命中都起著作用,於是也被添加進來(圖 4.2)。

圖4.2:解釋誰成為新首領的圖(左)和「生命圖」(右)
沙畫、記憶輔助工具和繪畫圖案
一種常用的畫圖技術是從放置幾個點開始,然後移動,就好像一條曲線圍繞著這些點編織一樣。矩形「框架」的內邊緣被認為是鏡子,曲線在那裏反彈,就好像是一束光線。接下來,在圖中放置一些額外的鏡子,以生成所需的曲線(圖4.3)。

圖4.3:五行六點和兩面「鏡子」(左),由一束假想的光線穿過,而方格則依次被染成黑色、白色、黑色、白色等等(中間),以產生最終的圖案,讓人聯想到非洲織物
圍繞這些點構建了一個矩形網絡,使這些點位於網絡線的交叉點上。在我們的插圖中,如果從左下方以45°角插入一束光線,從矩形框下邊框的第一個細分點開始,這束光線將描述一條假想的路線,在右上角以極小的路徑反彈到右邊,然後貼著右邊框返回到左下角,以此類推。
當假想光線穿過網絡時,一個方格會被染成黑色,然後是白色,接著又是黑色,依此類推,直到整個網絡都被染上顏色。最後,就形成了一個幾乎無法辨認出原始曲線的圖案。這讓人想起非洲的織物。
可以用不同的方法排列假想鏡面,或者使用更多或更少的點,結果也會不同。在圖論中,獲得正方形圖案的程式(此處使用黑白方框)有時會顛倒過來。例如,在對國際棋盤上的走子進行數學研究時,就采用了這種方法。
非洲繪圖專家熟練而毫不猶豫地繪制了這些圖形。這裏的座標系是一種記憶法,將記憶任務簡化為幾個數碼和一種幾何演算法(圖 4.4)。

圖4.4:來自其他初始條件的其他曲線
沙畫推理
瑪西婭·阿舍爾(Marcia Ascher, 1988, 1994)是最早關註這些沙畫及其與圖論關系的人之一。她列出了來自不同大陸的類似圖畫的清單,並根據地區或人物對圖畫進行了分類。她還註意到一些數學性質的特性,如圖形的倍增(圖 4.5)。

圖4.5:倍增圖形
米烏博人用一些點表示祖先,用其他點表示村莊的小屋。周圍的線表示祖先的靈魂影響著部族的生活。當居民人數增加時,圖畫就必須進行調整,這就是所謂的 「 倍增」圖。在其他例子中,圖形甚至可以有三重 倍增。
阿舍爾探索的另一個受數學啟發的特性是圖畫中的對稱性,如左右、雙重左右或旋轉對稱。許多例子表明,對圖畫進行不同的分組,例如按照所用點的數量進行分組,可能會很有趣。然而,結構並不總是那麽合乎邏輯、簡單明了。非洲人的創造力再次展示了令人驚訝的替代方案(圖4.6 和4.7)。

圖4.6:按照點的數量排列的圖畫。省略或增加一個點可以得到括弧中的類似情況

圖4.7:完全不同的對稱繪圖方法
沙畫中的更多數學
當哲學家路德維希·維特根斯坦(Ludwig Wittgenstein)試圖為數學的本質下定義時,他指出了圖論,並斷言 「每個人都會立即認識到它的數學特性」。與阿舍爾幾乎同時開始從事民族數學研究的保盧斯·格迪斯(Paulus Gerdes)試圖為這些非洲曲線提出一些真正的數學定理(Gerdes, 2002)。
與歐拉橋的第一個例子相比,格德斯采用了不同的矩陣方法。受之前推匯出的顏色模式的啟發,0 現在對應於正方形的一種給定顏色,1 對應於另一種顏色,如果需要第三種顏色,則對應於 2,以此類推(圖 4.8 和 4.9)。

圖4.8:作者為Gerdes 的一本著作撰寫的前言(Gerdes,2001 年)
圖4.9:根據非洲沙曲線圖案推匯出的矩陣
可以將兩個這樣的矩陣相加,從而形成一個新的模式(圖4.10)。

圖4.10:矩陣加法和色彩圖案
格德斯研究過一種特殊的安哥拉Lunda 圖畫,他以自己女兒的名字將其稱為「Liki 圖案」。插圖(圖 4.11)中展示了這樣一個Liki 圖案及其相關的矩陣。

圖4.11:從非洲沙曲線圖案推匯出的Liki矩陣
格德斯的Liki矩陣具有以下特性:
1. 沿著邊界,每個「主要」網格點(圖中粗體黑點)總是有兩個不同顏色的相鄰方格。
2. 任意相鄰的兩個「主要」網格點之間(垂直或水平方向)的四個單位方格中(縱向或橫向)之間的四個單位方格中,相鄰的兩個方格總是一種顏色、 而另外兩個則是另一種顏色(圖4.12)。

圖4.12:Liki 內容示意圖
根據Gerdes的觀點,這兩個性質意味著正方形利基設計是由迴圈組成。下面以網格點數為3×3的Liki 設計為例進行說明 (圖4.13)。
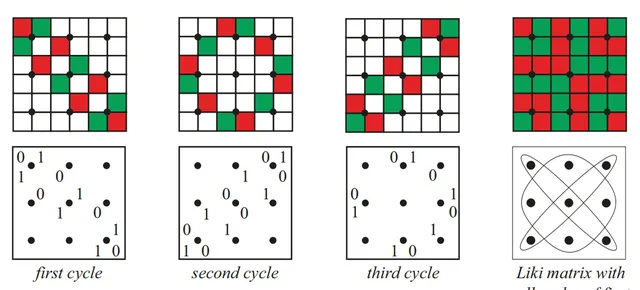
圖4.13:Liki 迴圈
通常的矩陣乘法將這些由0和1組成的矩陣轉化為不再包含0和1的矩陣,然而格德斯在這些方形Liki 矩陣中發現了一些非凡的特性(圖 4.14)。
圖4.14:二階結構
定理
Liki 矩陣A和B相交: AB=BA.
定理
AB具有二階迴圈結構(見插圖)。
格爾德斯將這些定理擴充套件到具有更多光柵點的矩陣,並就這些性質提出了其他變式。這可能是更常見的數學分析在這些沙畫上的初步套用。
形式、形狀及其分析
一些建築師和數學家喜歡在古典建築和繪畫作品上畫各種矩形、三角形和圓形。希臘神廟、中世紀大教堂或達芬奇的作品都是這些所謂「研究」的最愛。在這種「分析」中起重要作用的是所謂的黃金分割數ϕ(也稱黃金分割、黃金比例或神聖比例)。當長度為 x (>1) 的線段被分成長度為 1 和 x - 1 的兩部份,並且這種分割使得比例 (x - 1)/1 等於比例 1/x 時,它就出現了。這意味著一元二次方程式 x2 - x - 1 = 0,其中 (1 +√5)/2 = 1.6180... = ϕ是正解。長度為 0.618...的較小部份 x - 1 稱為小數,長度為 1 的較長部份稱為大數。
寬為1、長為ϕ的矩形被稱為黃金矩形。發現黃金矩形,甚至在不可能出現黃金矩形的情況下發現黃金矩形,是一些偽科學家最喜歡做的事情。一些雕像的頭在很久以前就被砍掉了,但雕像的雕刻者卻用黃金分割來解釋這些雕像,就好像雕刻者有預知能力,知道雕像的頭會被砍掉一樣。羅馬尼亞外交官馬蒂拉·吉卡(Matila Ghyka)是黃金分割神話的煽動者之一,他的弟子們成功地用四種不同的方式為同一神廟制作了黃金分割。在第一幅圖中,一些黃金分割大師從較低的階梯開始,另一些則從第二階梯開始,或者從第三階梯開始,最後一些則以神廟的腳為最低點進行繪制(圖4.15和4.16)。

圖4.15:按照黃金分割定律,左邊的矩形「太扁」,右邊的矩形「太方」,而中間的矩形是「理想形狀」。
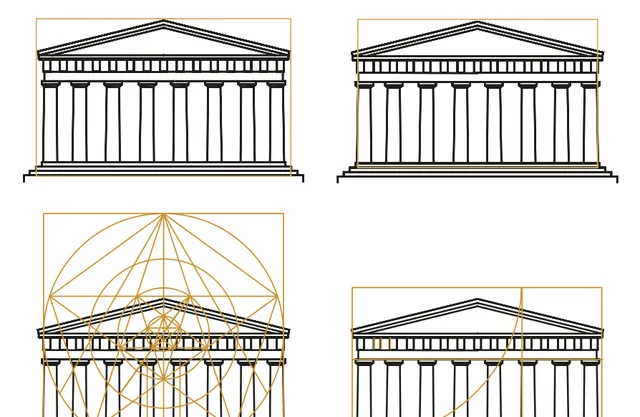
圖4.16:在同一棟建築中「發現」黃金分割的四種不同方法。這說明這些偽科學研究缺乏嚴謹的方法
各種書籍一遍又一遍地重復著這些圖畫,卻對某些圖畫相互矛盾的事實毫不關心。面對「在寺廟上畫一個黃金矩形」的練習,學生只有在與考官的觀點完全一致時才能透過考試。缺乏批判性思維可能是由於這些說法似乎具有可接受性。它們似乎強調了希臘古典文明、文藝復興以及(部份)實際西方文化的重要性。透過發現藝術表現形式中反映出的有理有據的思想證明,黃金部份有助於支持歐洲優越性的假象。在1984年重新出版的一本帶有豪華彩色封面的書中,法國作家D. Neroman認為希臘雕像是理想中的美,而非洲人和猶太人則「尚未成熟」,因為肚臍的高度與肚臍和頭頂之間距離的比例小於黃金比例(圖 4.17)。

圖4.17:尼羅曼對希臘、非洲和猶太婦女肚臍高度的研究,以及具有大小比例的塞努弗雕像
不幸的是,其他人對這一神話的反應是類比地「發現」非洲藝術中最奇妙的黃金分割。他們以同樣的創造力,在非洲物品中發現了金色的矩形和主次線段。當然,這並不難,因為非洲藝術和西方藝術一樣,也可以運用類似的幻想。另一方面,這也是值得贊賞的,因為藝術頭腦對數學啟發的主題樂此不疲是相當罕見的。然而,這與科學或數學無關。此外,對於新興的民族數學領域(該領域本身仍飽受批評)來說,在這種險惡的道路上誤入歧途是非常不明智的。
數學書籍中的非洲圖形
對非洲藝術形式的研究並不流行,因為人們普遍認為非洲藝術只是感性的(不管這意味著什麽)。這種觀念的根源或許是非洲人在20世紀60年代初發出的感嘆:「歐洲給了我們理性,非洲給了我們情感。」如果這句話是正確的,那麽它將支持這樣一種觀點,即非洲的藝術表現形式幾乎純粹是感性的表現,而歐洲的藝術則更多地基於理性的思考。這種偏見仍然占主導地位,可能阻礙了許多人對非洲雕塑采取技術起草的方法。我們在此不討論這種說法,因為下面的例子清楚地說明了相反的情況是完全可能發生的。
【數學教師】是美國國家數學教師委員會出版的一本雜誌,曾刊登過一些非洲插圖 (Zaslavsky,1970年)。該雜誌強調了創造性與數學教學之間的關系,並將形式與特定的數學曲線進行了比較(圖4.18和4.19)。
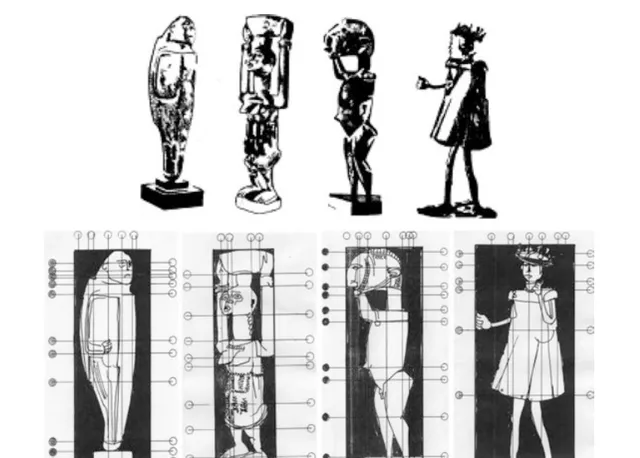

圖4.18:盧旺達Nyundo藝術學校使用的合理形式分析範例

圖4.19:來自雜誌【數學老師】的兩幅插圖
來自雅恩德的Njock教授是一位非洲科學家,他對數學和藝術對非洲大陸的重要性持有強烈的看法(Njock,1976 年,1979 年):
非洲藝術為世界開啟了黑非洲社會和文化歷史的基本視角:它塑造了兩千多年的歷史。[……]純數學是一門創造和想象的藝術。因此,黑藝術本質上是數學的。事實上,它刺激整個人格,道德和認知的可能性,想象力和創造性的態度。在分析黑藝術的貢獻時,人們不能忽視個人的知識,或者無數的情感和想象。[…]
公認的教學理論指出了想象力和欣賞的巨大好處。人們最終會想到教育者所允許的自由藝術表達的重要性,透過自發的活動表達自我和強調每個人的獨創性的必要性,證明人類思想的創造性前進演化的重要性,不僅作為藝術活動的基礎,而且作為人類生活的一個方面。黑藝術是宇宙文明宏偉結構中最重要的部份之一。
幾何圖案
有些編織物的靈感似乎來自數學。加納的阿散蒂人在編織品中大量使用幾何圖案,象牙海岸和布基納法索也有許多類似的編織品(圖 4.20)。

圖4.20:西非的織布機和縫紉機精細編織的織物
這裏也有描述織物及其特殊名稱的故事。因此,「之」字形邊線意味著旅行者將永遠回家。不過,這些圖案並不總是從幾何圖形中獲得靈感,而往往是出於簡單的實用性。例如,它們通常是在小型織機上織成的,這可能就是阿散蒂織品的飄帶的由來。之後,它們被簡單地縫合在一起,形成較大的織物。一個有趣的現象是,現代非洲紡織品仍在模仿這些條紋圖案,盡管如今它們是一體成型的,因此沒有與小條紋相關的技術要求(圖 4.21、4.22、4.23 和 4.24)(Pauwels,1952年)。

圖4.21:模仿條紋圖案的現代阿散蒂布料

圖4.22:帶有抽象裝飾的盧旺達小屋內景

圖4.23:Pauwels的盧旺達繪畫清單;數碼表示相關說明

圖4.24:盧旺達的傳統伊米貢戈畫
在國際上,阿散蒂的繪畫是最著名的,盡管它們在聲譽上可以與南非的繪畫相媲美。在中非,許多圖畫和圖案也可以在小屋周圍的圍欄上、籃子上、蓋子上、牛奶罐上和鼓的裝飾品上找到。
「純粹的"繪畫
比利時數學家塞利斯在盧旺達逗留期間曾想過,為什麽幾何圖形、非具象圖畫比人物和動物圖片或故事插圖更受歡迎(Celis,1972年)。他特別在該國東南部的一個偏僻地區觀察到了這一現象。該地區過去交通不便,因此人們認為大多數圖畫都是原始的傳統概念,而不是與其他文化交流的結果,也不是持續文化融合的結果。
用所謂的伊米貢戈裝飾小屋的現象似乎可以追溯到大約300年前。口述描述了傳說中著名的卡基拉·卡·基梅尼(Kakira ka Kimenyi)如何引入裝飾小屋墻壁的傳統(圖 4.25)。
圖4.25:上圖中的圖案
卡基拉·卡·基梅尼(Kakira ka Kimenyi)一生中的許多事跡表明,他對純潔的理念非常癡迷;他的牛被關在小屋裏,也在那裏宰殺,這樣就不會有蒼蠅飛到它們身上[......]他討厭泥濘,在大雨中坐在石頭上。他的整潔是如此傳奇,以至於 「isuku ni ya Kakira 」或「像 Kakira一樣整潔」成了一句諺語。
卡基拉擁有豐富的創作經驗,他制作這些畫作的目的無非是為了自己欣賞和保持整潔;他先是為父親制作這些畫作,[......]然後又為自己的小屋制作這些畫作。[......]他自己畫了這些畫後,鼓勵貴族少女們模仿他的想法。就這樣,畫作流傳開來。
G. Celis 和 T. Celis 註意到,他們遇到的所有圖案都是由幾種基本結構組合而成的。垂直和水平方向,加上三條斜線及其與垂直軸的對稱方向,就足以構成所有圖案。有了這八個方向,「伊米貢戈 」就可以簡化為幾種情況,只有平行線、菱形、等腰三角形和等邊三角形起作用。
巧合的是,這些幾何觀察結果導致某些圖畫因沒有遵循規定的規則而被視為非原創而遭到拒絕(見第12章)。還有人利用卡基拉規則為電腦編程,從而創造出傳統上正確的圖案。具有諷刺意味的是,以純粹著稱的Kakira ka Kimenyi偏愛抽象,卻為數學這門「純粹」的科學做出了貢獻。
飾帶圖案與晶體學
J. 威廉士為使用中國、阿拉伯和非洲繪畫來教授6-16歲的學生辯護:
晶體學研究的是按照對稱組別對圖案進行分類,但多文化圖案和設計例項也能說明這一點。紮斯拉夫斯基復制了一幅剛果巴庫巴人的刺繡布(現藏於大英博物館),其中完整地收集了7種不同的一維飾帶紋(即希臘神廟上的條狀線形圖案)。這些圖案與一維變換有關,如 180°旋轉以及水平糊垂直反射。利用群論可以證明,這樣的圖案只能存在7種。
使用所謂的群論是一種更加數學化的欣賞非洲幾何圖形的方法,而不是對各種圖畫進行簡單的描述性清點,解釋它們的形狀、目的或解釋。例如,數學家可以利用群論證明,就圖案的對稱性而言,只有7種飾帶圖案是可能的;如果圖案中允許有一種顏色,那麽可能性就會增加到24種。至於(非彩色的)二維圖案,即平面圖案,則有 17 種數學圖案是可能的。D. Crowe 研究了剛果巴庫巴人和貝寧人藝術中的重復圖案(Crowe,1975 年)。在飾帶圖案中,他發現了所有7種可能性的例子,但在平面圖案中,17種可能性中只有12種(圖 4.26)。
圖4.26:在貝寧可以找到所有7種數學上可能的飾帶圖案
非洲碎形
在流行數學中,碎形是眾所周知的,這可能是因為它們可以用漂亮的圖畫來表示,讓人聯想起雲朵、蕨類植物、菜花或迷幻MTV影片的形狀。這一概念已有100多年的歷史,但多虧了法國人 B. Mandelbrot(移居美國),這一數學課題才得以擺脫數學象牙塔的束縛,得到媒體的充分關註(圖4.27和4.28)。
圖4.27:這種碎形是為了紀念Benoit Mandelbrot而命名的,他在媒體中普及了這個話題
圖4.28:描述【非洲碎形:巴伊拉聚落的碎形解釋】一書的插圖
就像蕨類植物的葉子一樣,碎形也有這樣的特性,即放大後的新影像與原影像一模一樣。這種放大一直到無窮大,因為對於碎形來說,較小尺度上的圖畫的定義來自較大尺度上的圖畫。這就是為什麽碎形的「觸角」看起來越來越小的原因。當它們或多或少地覆蓋平面或填充空間時,就會產生所謂的碎形維度。對於表面上的碎形曲線來說,這個維度介於1(直線)和 2(表面的維度)之間,而對於空間碎形來說,這個維度介於2和3(空間的總維度)之間。例如,在一件非常保暖的毛衣中編織的線當然是一維的,但它卻形成了一個幾乎是二維的交錯曲面。碎形似乎可以用非常簡單的數學表述來描述自然現象。
著名的非裔美國科學家本傑明·班奈克(Benjamin Banneker)使用了一種所謂的五邊形碎形。在塞內加爾,經常可以看到這種碎形圖案作為裝飾出現在脖子上的小皮包上。埃塞俄比亞的十字架是重新發現數學碎形結構的其他例子(圖 4.29)。
圖4.29:塞內加爾皮包上的班奈克碎形(上圖)和埃塞俄比亞十字架上的班奈克碎形
不過,要在非洲人的發型或雕像上看到碎形,還需要更多的想象力。當然,只要這些碎形在算術和幾何上是正確的(前面提到的黃金分割之謎就不是這樣),這樣的練習就沒有什麽問題。朗·埃格拉什寫了一整本關於非洲碎形的書。可以說,許多非洲圖形的靈感都來自大自然和生活場景,因此這些圖形都包含了大自然的碎形結構(圖 4.30)。
圖4.30:用碎形解釋非洲雕像
另一方面,大衛·阿夫尼爾(以色列耶路撒冷希伯來大學)等科學家已經證明,自然界的碎形內容是值得商榷的:很多時候只有兩個或三個尺度層次,而無限延續的可能性是碎形定義的一部份。在埃格拉什所謂的非洲碎形中,通常也最多只有三個層次。阿夫尼爾甚至親自寫信給曼德布羅特,反對他對自然的碎形解釋。他們的討論沒有得出明確的結論。柏德烈·福勒(Patrick Fowler)在私人信件中說了一句風趣的話: 「為什麽沒有一本關於'天主教碎形'的書呢?因為在某些宗教藝術中,聖人手捧聖母瑪利亞像,懷抱耶穌聖嬰。那也是碎形藝術嗎?這樣的雕像能證明天主教藝術家在600年前發明了碎形嗎?同樣,也許還有印度教或維京人的碎形(圖 4.31)。
圖4.31:天主教、印度教和維京人的民族數學碎形
因此,無論如何,這裏有一個沙子曲線、繪制圖案和碎形優雅交匯的例子。格 德斯運用數學想象力,從非洲沙地曲線出發,首先將其轉化為繪畫圖案,從而得到了一個碎形(圖 4.32)。
圖4.32:由簡單沙粒曲線圖案得到的格德斯碎形
青山不改,綠水長流,在下告退。
轉發隨意,轉載請聯系張大少本尊。











