任意兩點之間的距離都是整陣列成的集合,它是什麽樣子?這個看似簡單的問題在Norman Anning和Paul Erdős 80年前取得結果後幾乎沒有進展。現在,三位數學家將組合學、數論和代數幾何聯系在一起,將問題變得更為復雜,結果卻闡明了它應有的結構。
撰文 | Erica Klarreich
轉譯 | zzllrr小樂
如果一個大型(但非無限的)點集中的點,彼此之間的距離都是整數,那麽這些點該如何排布呢?一個最新的結果證明,圓形是僅有的可能選項之一。丨圖源:Fran Pulido/Quanta Magazine
計劃的改變發生在一次公路旅行中。去年四月風和日麗的一天,數學家瑞Rachel Greenfeld和Sarah Peluse從她們的單位——新澤西州普林斯頓高等研究院出發,前往紐約州的羅切斯特,她們兩人都被安排在第二天發表演講。
她們近兩年來一直在努力解決調和分析領域的一個重要猜想,該領域研究如何將復雜訊號分解成分量頻率。她們與第三位合作者Marina Iliopoulou一起,研究了這樣一個問題:其中各分量頻率被表示為平面上的點,而這些點之間的距離與整數相關。這三名研究人員試圖證明這些點的數量不可能太多,但到目前為止,她們所有的方法都失敗了。
她們似乎在原地打轉。Peluse靈機一動:如果暫時放棄調和分析問題,將註意力轉向任意兩點之間距離正好為整數的點集會怎樣?這樣的點集可能具有什麽結構呢?自古以來,數學家們一直在試圖理解整數距離集。例如,勾股陣列 (即畢達哥拉斯三元組,例如3, 4和5) 表示直角三角形,其三個頂點之間的距離都是整數。
「坐在車裏,我猜是因為Rachel和我在一起,我提出了這個想法,」現任密芝根大學教授的Peluse說。解決整數距離集的想法讓Greenfeld興奮不已。
在意識到這一點之前,她們已經兩次走錯了方向。
「我們其實沒有註意到正在往哪裏開車,也沒有離開高速公路,」Peluse說。「我們朝著與羅切斯特相反的方向上行駛了大約一個小時才留意到,因為我們太興奮了。」
1945年,Norman Anning和Paul Erdős證明 [1] ,平面上滿足任意兩點距離均為整數的無限點集必位於一條直線上(共線) 。對於一個有限點集,可能性更加多樣化。數學家們已經構建了位於直線或圓上的大型點集,有時還有三四個例外的點偏離主線。 (點本身不必具有整數座標——只在乎它們之間的距離是整數。)

Rachel Greenfeld普林斯頓高等研究院數學家丨圖源:Andrea Kane
沒有人提出具有任何其他結構的大型點集,但也沒有人證明其他結構是不可能的。自從Anning和Erdős的結果發表以來的近80年裏,這個課題幾乎沒有任何進展——直到現在。
Greenfeld、Iliopoulou和Peluse已經證明 [2] ,一個大型整數距離點集的所有點——也許除了少數幾個異常點之外——必位於一條直線或圓上。「如果你想要一個所有點成對距離都是整數的大型集合,那麽圓形和直線是唯二的可能,」卑詩大學的József Solymosi說。他稱她們的結果為「絕妙的解決方案」。
這種新方法使用了來自數學三個不同領域的思想和技巧:組合學、數論和代數幾何。這些不同領域的結合「可能是一個真正的心理突破」,加州大學洛杉磯分校的數學家陶哲軒說。
羅切斯特大學的Alex Iosevich對此表示贊同。「她們為一系列非常廣泛的問題奠定了非常堅實的基礎,」他說。「在我看來,毫無疑問,這將找到更深層次的套用。」
簡單性的局限
在平面上,選擇一個所有點之間距離都是整數的無限集合是很容易的——只需取你最喜歡的一條直線,想象一條數軸線疊加在上面,並標出對應於整數的所有或部份點。但正如Anning和Erdős在1945年就認識到的那樣,這是在平面上構建無限整數距離點集的唯一方式。一旦你有三個點不在同一直線上,你的配置就會變得受限,從而不可能無限添加其他點。
原因可以歸結為簡單的幾何學。假設距離為整數的兩點A和B,如果你想添加第三點C,它到A和B的距離都是整數,但不在過A和B的直線上,那麽平面上的大多數點都不適用。可行的點位於特殊曲線上,這些曲線稱為雙曲線(hyperbola),它們從A和B之穿過。如果A和B之間的距離是4個單位,那麽恰好有四條這樣的雙曲線。 (雙曲線通常有兩個不同的部份,例如下面的兩條紅色曲線形成一個雙曲線。)
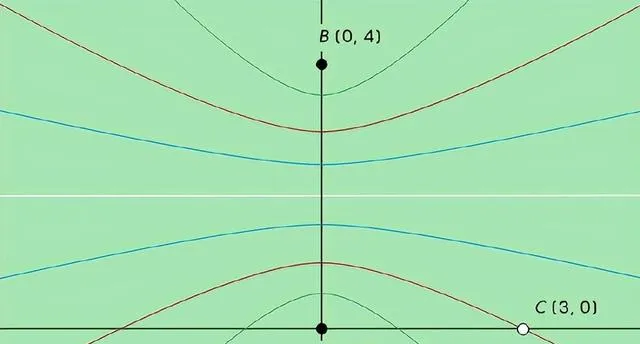
圖源:Merrill Sherman/Quanta Magazine
一旦在你選擇了C (如上圖,C到A的距離是3個單位,到B的距離是5個單位) 之後,你幾乎沒有更多的選擇來添加更多的點。你能添加的任何點必須位於A和B之間的某條雙曲線上,或者位於透過它們的直線上。但它也必須位於A和C之間的某條雙曲線上,以及B和C之間的某條雙曲線上 (或相應的直線上) 。換句話說,一個新的點只能放在三條雙曲線或直線的交點處 (盡管並非每個交點都適用) 。一開始,這些雙曲線和直線只有有限多的個,而兩條雙曲線 (或直線) 最多在四個點上相交。所以你最終只能從有限數量的交點中選擇——你不能構建一個無限集合。
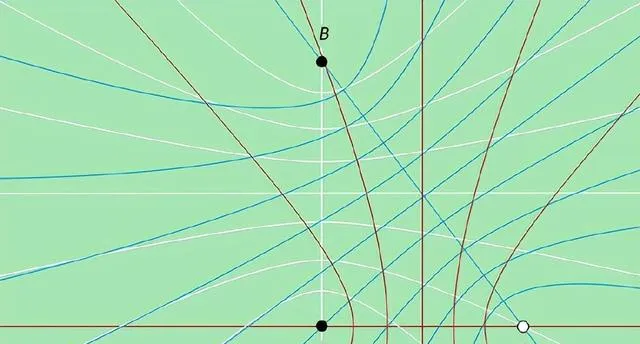
當你想要理解一個整數距離的有限點集實際上是什麽樣子時,雙曲線方法很快就會變得難以駕馭。隨著點的數量增加,你必須應對越來越多的雙曲線。例如,當你的集合中有10個點時,添加第11個點將建立10個新的雙曲線家族——所有這些新的雙曲線都在你新加的點和集合中已有的每一點之間。Greenfeld說:「你不能添加很多點,因為你會迷失在所有這些雙曲線和交點中。」
因此,數學家一直在尋找更易於駕馭的方法來構建不位於直線上的整數距離點集。但他們只找到了一種方法:把點放在一個圓上。如果你想要一個有萬億個點的整數距離點集,有辦法在一個半徑為1的圓上找到萬億個點,這些點之間的距離都是分數。然後你可以擴大這個圓,直到所有的分數距離都變成整數。你想要的集合中的點越多,圓就需要擴得越大。
多年來,數學家們只找到了稍微奇特一些的例子。他們可以構造出大型的整數距離點集,除了四個點外,所有點都在一條直線上;或除三個點外,所有點都在一個圓上。許多數學家懷疑這些是僅有的大型整數距離點集,其中並非所有點都在一條直線或一個圓上。如果他們能夠證明所謂的Bombieri-Lang猜想,他們將對此確信無疑。但是數學家們對於這個猜想是否可能成立持有不同意見。
自1945年Anning和Erdős的工作以來,數學家在理解整數距離點集方面幾乎沒有取得進展。隨著時間的推移,整數距離問題似乎並入了組合學、數論和幾何學中的一系列其他問題,這些問題簡單易懂,但似乎不可能解決。陶哲軒說:「這是衡量我們的數學有多可憐的一種方式。」

Sarah Peluse,密芝根大學數學家丨圖源:Dan Komoda
從某種意義上說,整數距離問題是其早期成功的受害者。雙曲線證明及其巧妙的簡單性,正是Erdős所信奉哲學的典型代表,Erdős是一位非常有影響力的數學家,他經常談到「The Book」——一個假想的收錄數學中最優雅證明的書卷。Erdős推崇的簡潔性文化在組合幾何學中取得了「巨大的成果」,Iosevich說。但這也可能導致盲點——在這個案例中,是關於引入代數幾何方法的價值。
「我認為在過去50年裏,你不會找到一個不涉及很多技術性和復雜內容的代數幾何的結果,」Iosevich說。「不過,有時候就需要這樣做。」
回過頭來看,整數距離問題一直在等待那些願意考慮比雙曲線更不規則的曲線,並利用來自代數幾何和數論的深奧工具來馴服它們的數學家。「這需要具備足夠知識和興趣的人,」Iosevich說。
Iosevich說,大多數數學家滿足於在整個職業生涯中只在某個數學領域使用幾種工具。但Greenfeld、Iliopoulou和Peluse是無畏的探險家。「她們認為數學是一個連貫的整體。」
問題復混成
在2021年夏天,Greenfeld決定是時候嘗試解決一個她自研究生以來一直在思考的調和分析問題。古典調和分析,構成了現實世界中訊號處理的基礎,其核心是將訊號分解為不同頻率和相位的正弦波。這一過程之所以有效,是因為可以得出一個無限的正弦波列表,當它們組合在一起時,可以捕捉到任何訊號的所有特征,而不會有任何冗余。
然而,研究者們通常想要研究比一維訊號更復雜的東西。例如,他們可能想要分解平面上的一個圓盤上的訊號。但是,圓盤只能承載有限數量的相容的正弦波——不足以捕捉圓盤上所有可能訊號的行為。於是問題變成了:這個有限集合可以有多大?
在這樣的集合中,正弦波的頻率可以用平面上的點來表示,這些點似乎不願在直線和圓上聚集:你永遠不會找到三個點都靠近同一直線,或四個點都靠近同一個圓。Greenfeld希望利用這種排斥性來證明這些頻率集合只能包含幾個點。
在2021年波恩大學的一次會議上,Greenfeld參加了一個關於「行列式方法」 (determinant method) 的講座,這是來自數論的一種技術,可以用來估計在曲線上某些類別的整數點可以有多少個。她意識到,這個工具可能正是她需要的。Greenfeld邀請了也參加會議的Iliopoulou和Peluse。「我們開始一起學習這個方法,」Greenfeld說。
但是,盡管做出了許多努力,她們似乎無法將行列式方法套用於她們的問題上,到了2023年春天,她們感到灰心喪氣。Iosevich邀請Greenfeld和Peluse開車去羅切斯特進行存取。「所以我們想,‘好吧,我們會去羅切斯特,和Alex談談會讓我們重新振作起來,’」Peluse說。但結果卻是,因為在賓夕法尼亞州薩斯奎哈納河 (Susquehanna River) 沿岸的意外繞行中討論整數距離點集,她們在到達羅切斯特時已經重新振作了起來。
她們到達時錯過了計劃與Iosevich共進的晚餐,但她們在酒店大堂找到了正在等她們的Iosevich,他手上拿著大包小包的外賣。他原諒了她們的遲到,而且第二天早上,當她們告訴他計劃解決整數距離點集時,他更顯寬容。「他非常興奮,」Peluse回憶道,「他在情感上給了我們巨大的鼓舞。」

Marina Iliopoulou,雅典大學的數學家丨圖源:由Marina Iliopoulou提供。
就像雙曲線方法一樣,Greenfeld、Iliopoulou和Peluse試圖透過辨識點必須所處的曲線家族來控制整數距離點集的結構。一旦點的數量增多,雙曲線方法就會變得過於復雜,但Greenfeld、Iliopoulou和Peluse想出了如何透過將整個配置移動到更高維空間來同時考慮數量較多的點。
這是如何實作的呢,假設整數距離點集中有一個「參考」點A,集合中其他每一點都與A有一個整數距離。這些點位於一個平面上,但你可以透過給每一點添加一個第三座標 (其值是到A的距離) 將平面彈到三維空間中。例如,假設A是點 (1, 3)。那麽,到A距離為5個單位的點 (4, 7) 在三維空間中變成了點 (4, 7, 5)。這個過程將平面轉換成三維空間中的一個錐形,其頂點是A,此時標記為 (1, 3, 0)。整數距離點變成了三維空間中的點,這些點位於錐形上,同時也位於某個格點上。
同樣,如果選擇兩個參考點A和B,你可以將平面上的點轉換到四維空間中——只需給每一點兩個新的座標,其值是它到A和B的距離。這個過程將平面轉換成四維空間中的一個曲面。你可以繼續以這種方式添加更多的參考點,每增加一個新的參考點,維數就增加1,平面就對映到一個更加蜿蜒的曲面 (或者,數學家稱之為更高次的曲面) 。
有了這個框架,研究人員使用了來自數論的行列式方法。行列式是與矩陣相關聯的數,它們刻畫了一組點的許多幾何內容——例如,一個特定的行列式可能度量了由三個點形成的三角形的面積。行列式方法提供了一種估計同時位於蜿蜒曲面和格點上的點數的方法——這正是Greenfeld、Iliopoulou和Peluse所處理的情況。
她們利用基於行列式方法的一系列工作證明,當整數距離點集被提升到適當的高維度時,點必須都位於少數幾條特殊曲線上。這些曲線,當它們的陰影在平面上不是直線或圓時,就不能包含許多格點 (lattice points) ,而這些格點是整數距離點集中的點的唯一候選者。這意味著集合中可能位於主線或圓之外的點的數量是有限的——研究人員證明,這個數量必須小於一個關於集合直徑的非常緩慢增長的函數。
它們的界限並沒有達到許多數學家認為對於大型整數距離點集來說正確的「四點離線或三點離圓」猜想的標準。即使如此,這一結果表明,「猜想的本質是正確的,」史丹福大學的Jacob Fox說。數學家們表示,這個猜想的完整證明可能需要另一種新思路的註入。
Iosevich說,團隊的高維編碼方案「極其穩健」。他說:「不僅僅是在原理上,我已經開始考慮實際套用了。」
Greenfeld、Iliopoulou和Peluse希望,她們原始的調和分析問題將是一個套用。她們現在又回到這個問題上。她們關於整數距離點集的結果「可能是通向那個問題的墊腳石,」Greenfeld說。
Iosevich預測,研究人員開始將組合學與代數幾何相結合,這種結合不會止步於整數距離點集或調和分析中的相關問題。「我相信我們所看到的是一種概念性的突破,」他說。「這向兩個領域的數學家傳達了一個資訊,即這種互動非常富有成效。」
陶哲軒表示,這也傳達了一種資訊,有時使問題變得更加復雜也是有價值的。他指出,數學家們通常追求相反的目標。「但這是一個例子,其中復混成問題實際上是正確的做法。」
他說,這一進展改變了他對高次曲線的看法。「有時候,它們可以是你的朋友,而不是敵人。」
參考文獻
[1] https://www.ams.org/journals/bull/1945-51-08/S0002-9904-1945-08407-9/
[2] https://arxiv.org/abs/2401.10821
本文經授權轉自「zzllrr小樂」公眾號,原標題【小樂數學科普:融合領域,數學家們在老問題上走得更遠】;【返樸】對譯文進行了校訂。本文譯自Merging Fields, Mathematicians Go the Distance on Old Problem,原文連結:https://www.quantamagazine.org/merging-fields-mathematicians-go-the-distance-on-old-problem-20240401/。
特 別 提 示
1. 進入『返樸』微信公眾號底部選單「精品專欄「,可查閱不同主題系列科普文章。
2. 『返樸』提供按月檢索文章功能。關註公眾號,回復四位陣列成的年份+月份,如「1903」,可獲取2019年3月的文章索引,以此類推。











